2023版考前三个月冲刺专题练　第20练　空间向量与距离、探究性问题课件PPT

这是一份2023版考前三个月冲刺专题练　第20练　空间向量与距离、探究性问题课件PPT，共28页。PPT课件主要包含了规律方法等内容，欢迎下载使用。
考情分析空间向量与距离、探究性问题在高考试题中出现较少，一般以解答题的形式考查，难度在中档以上.
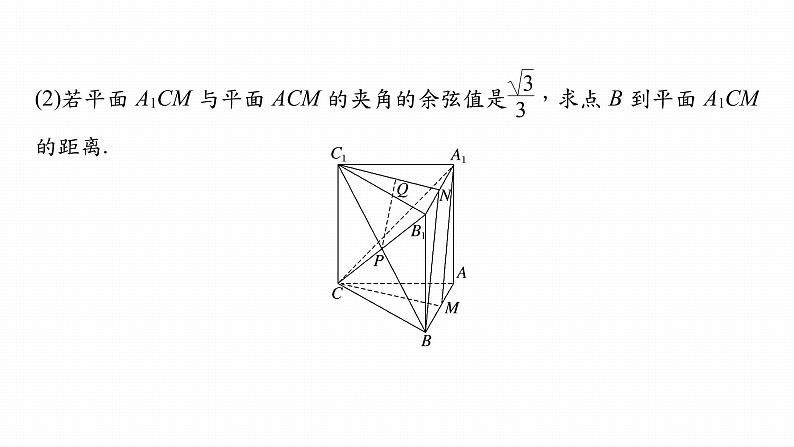
一、空间距离 (2022·吉林模拟)如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面A1B1C1，∠BAC＝90°，AB＝4，AC＝2，M是AB的中点，N是A1B1的中点，P是BC1与B1C的交点，点Q在线段C1N上.(1)求证：PQ∥平面A1CM；
如图，连接AC1交A1C于点H，连接MH.∵AH＝HC1，AM＝MB，∴BC1∥MH，又MH⊂平面A1CM，BC1⊄平面A1CM，∴BC1∥平面A1CM.∵四边形A1NBM是平行四边形，∴BN∥A1M，又BN⊄平面A1CM，A1M⊂平面A1CM，
∴BN∥平面A1CM.∵BC1∩BN＝B，BC1⊂平面BC1N，BN⊂平面BC1N，∴平面A1CM∥平面BC1N.又∵PQ⊂平面BC1N，∴PQ∥平面A1CM.
以A为原点， 所在直线分别为x轴，y轴，z轴的正方向，建立如图所示的空间直角坐标系，设A1(0,0，h)(h>0)，M(0,2,0)，C(2,0,0)，B(0,4,0)，
设平面A1CM的法向量为n＝(x，y，z)，
解得n＝(h，h，2).显然平面ACM的法向量可取为n0＝(0,0,1).
又h>0，解得h＝2，∴n＝(2,2,2).
(1)点到直线的距离直线l的单位方向向量为u，A是直线l上的任一点，P为直线l外一点，设 ＝a，则点P到直线l的距离d＝ .(2)点到平面的距离平面α的法向量为n，A是平面α内任一点，P为平面α外一点，则点P到平面α的距离为d＝ .
(2022·镇江模拟)如图所示，在三棱柱ABC－A1B1C1中，AB＝BC，点A1在平面ABC上的射影为线段AC的中点D，侧面AA1C1C是边长为2的菱形.
(1)若△ABC是正三角形，求异面直线DB1与BC所成角的余弦值；
依题意，点A1在平面ABC上的射影为线段AC的中点D，所以A1D⊥平面ABC，A1D⊥CD，A1D⊥BD，由于AB＝BC，所以BD⊥CD，以D为坐标原点建立如图所示空间直角坐标系，
设直线DB1与BC所成角为α，
(2)当直线CB1与平面ABB1A1所成角的正弦值为 时，求线段BD的长.
设平面ABB1A1的法向量为n＝(x，y，z)，
故可取平面ABB1A1的一个法向量为
设直线CB1与平面ABB1A1所成角为β，
化简得4t4－13t2＋9＝0，即(t2－1)(4t2－9)＝0，t>0，
二、探究性问题 (2021·全国甲卷改编)已知直三棱柱ABC－A1B1C1中，侧面AA1B1B为正方形，AB＝BC＝2，E，F分别为AC和CC1的中点，D为棱A1B1上的点，BF⊥A1B1.
(1)证明：BF⊥DE；
因为E，F分别是AC和CC1的中点，且AB＝BC＝2，
如图，连接AF，由BF⊥A1B1，AB∥A1B1，得BF⊥AB，
由AB2＋BC2＝AC2，得BA⊥BC，故以B为坐标原点，以BA，BC，BB1所在直线分别为x，y，z轴建立空间直角坐标系，则B(0,0,0)，E(1,1,0)，F(0,2,1)，
设B1D＝m(0≤m≤2)，则D(m，0,2)，
(2)当B1D为何值时，平面BB1C1C与平面DFE的夹角的正弦值最小？
易知平面BB1C1C的法向量可取为n1＝(1,0,0).设平面DFE的法向量为n2＝(x，y，z)，
令x＝3，得y＝m＋1，z＝2－m，于是平面DFE的一个法向量为n2＝(3，m＋1,2－m)，
设平面BB1C1C与平面DFE的夹角为θ，
空间向量求解探究性问题：(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论；(2)在这个前提下进行逻辑推理，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标(或参数)是否有解、是否有规定范围内的解”等.若由此推导出矛盾，则否定假设；否则，给出肯定结论.
　　 (2022·北京丰台模拟)如图，在直角梯形ABCD中，AB∥CD，∠DAB＝90°，AD＝DC＝ AB.以直线AB为轴，将直角梯形ABCD旋转得到直角梯形ABEF，且AF⊥AD.(1)求证：DF∥平面BCE；
由题意得EF∥CD，EF＝CD，所以四边形DCEF为平行四边形，所以DF∥CE，因为DF⊄平面BCE，CE⊂平面BCE，所以DF∥平面BCE.
线段DF上存在点P，使得直线AE和平面BCP所成角的正弦值为 ，理由如下：由题意得AD，AB，AF两两垂直.建立如图所示的空间直角坐标系.设AB＝2，则A(0,0,0)，B(0,2,0)，C(1,1,0)，D(1,0,0)，E(0,1,1)，F(0,0,1)，
设平面BCP的法向量为n＝(x，y，z)，
令x＝λ，则y＝λ，z＝1＋λ，于是n＝(λ，λ，1＋λ)，