2022届云南省高三下学期4月第二次高中毕业生复习统一检测（二模）数学（理）试题 word版

2022年云南省高三第二次省统考理科数学试卷

一、选择题：（本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项符合题目的要求的）

1.          设集合S={0,1},T={0,3}，则S∪T=（       ）
     A.{0}         B.{1,3}          C.{0,1,3}          D.{0,1,0,3}
2.          已知i为虚数单位，设，则复数z在复平面内对应点位于（    ）

1. 第一象限                    B.第二象限
2. 第三象限                    D.第四象限

3.已知是函数的两个零点.若，则（    ）

1.                     B.
2.                     D.

4.设为平面向量。若为单位向量，，的夹角为，则=（      ）

   A.             B.          C.            D.

5.若执行右边的程序框图，则输出的结果S=（       ）

1. -1         B.-3             C.-5              D.-7

6.某超市为庆祝开业举办酬宾抽奖活动，凡在开业当天进店的顾客，=都能抽一次奖，每位进店的顾客得到一个科不透明的盒子，盒子里装有红、黄、蓝三种颜色的小球共6个，其中红球2个，黄球3个，篮球1个，出颜色外，小球的其他方面，如形状、大小、质量等完全相同，每个小球上均写有获奖内容，顾客先从自己得到的盒子里随机抽取2个小球，然后依据取出的2个小球获奖内容去兑奖，设X表示某顾客再一次抽奖时，从自己得到的那个盒子里取出的2个小球中红球的个数，则X的数学期望E（X）=（          ）

  A.              B.              C.             D.

7.已知长方体的表面积为62，所有棱长和为40，则线段为（        ）

1.              B.            C.           D.

8.若则（      ）

1.                     B.
2.                     D.

9.已知等差数列{}的前n项和为，若，则数列{}的前N项和是（       ）

1.                      B.
2.                      D.

10.已知双曲线C的中心在坐标原点，焦点在x轴上，离心率等于，点（）在双曲线C上，椭圆E的焦点与双曲线C的焦点相同，斜率为的直线与椭圆E交于A、B两点，若线段AB的中点坐标为（1，-1），则椭圆E的方程为（        ）

1.                      B.
2.                      D.

11.

  A.3               B.4             C.             D.

12.三棱锥P-ABC的顶点都在以PC为直径的球M表面上，PA⊥BC，若球的表面积为100π，PA=8，则三棱锥P-ABC的体积最大值为（       ）

1. 24                         B.

C.27                         D.

二、填空题：（本题共4小题，每小题5分，共20分）

   13.若，则的值为=.

   14.设曲线关于直线对称，则=.

 15.设数列{}的前n项和为，若，，则数列{}的通项公式为=.

 16.已知e是自然对数的底数.若，使得，则实数m的取值范围=.

三、解答题：（共70分）

  17.（12分）

     △ABC中，内角A,B,C的对边分贝为a,b,c,D是AC的中点.已知平面向量满足.

（1）求A.

（2）若BD=,b+2c=4,求△ABC的面积.

18.    （12分）

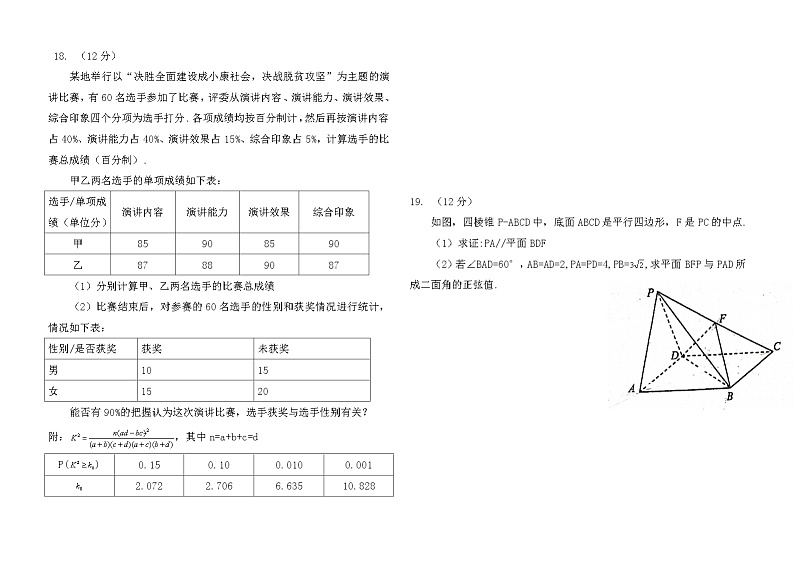
某地举行以“决胜全面建设成小康社会，决战脱贫攻坚”为主题的演讲比赛，有60名选手参加了比赛，评委从演讲内容、演讲能力、演讲效果、综合印象四个分项为选手打分.各项成绩均按百分制计，然后再按演讲内容占40%、演讲能力占40%、演讲效果占15%、综合印象占5%，计算选手的比赛总成绩（百分制）.

甲乙两名选手的单项成绩如下表：

（1）分别计算甲、乙两名选手的比赛总成绩

（2）比赛结束后，对参赛的60名选手的性别和获奖情况进行统计，情况如下表：

能否有90%的把握认为这次演讲比赛，选手获奖与选手性别有关？

附：，其中n=a+b+c=d

19.    （12分）

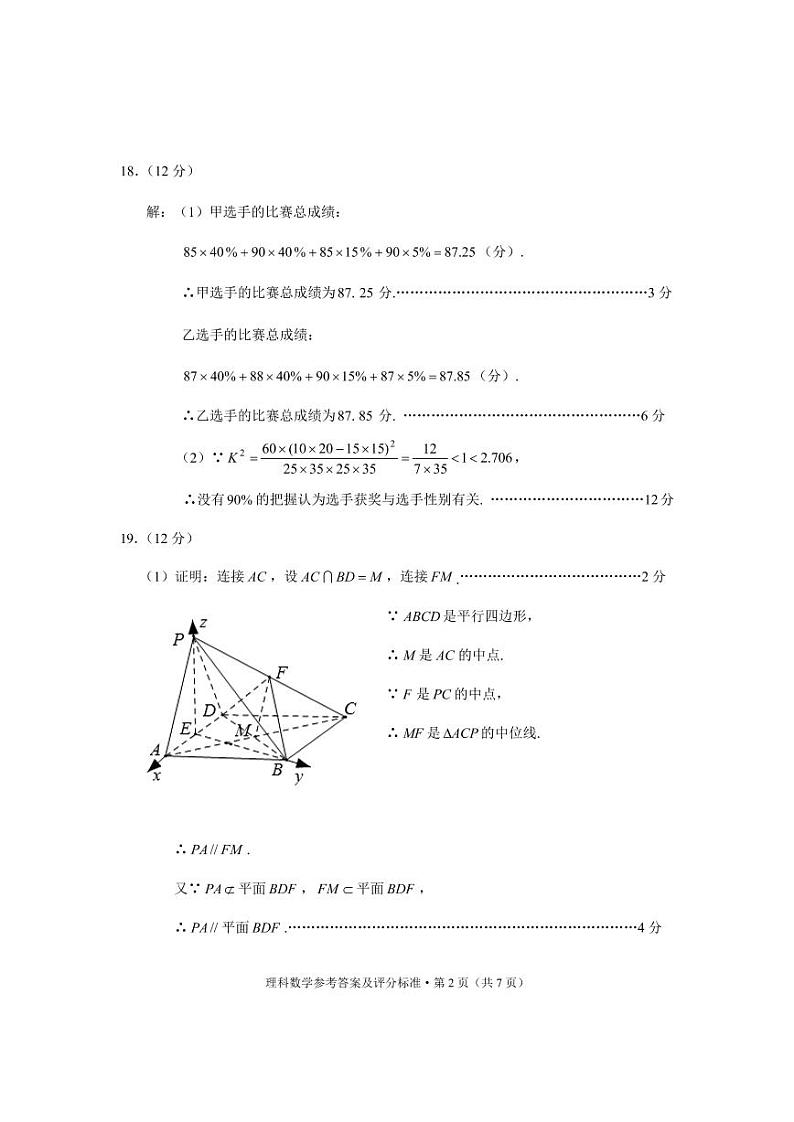
如图，四棱锥P-ABCD中，底面ABCD是平行四边形，F是PC的中点.

（1）求证:PA//平面BDF

（2）若∠BAD=60°，AB=AD=2,PA=PD=4,PB=,求平面BFP与PAD所成二面角的正弦值.

20.    （12分）

   已知e是自然对数的底数，，常数a时实数

（1）设a=e，求曲线在嗲（1，f(1)）处的切线方程。

（2）都有，求a的取值范围.

21.    （12分）

     已知曲线C的方程为，点D的坐标为（1,0），点P的坐标为（1,2）.

（1）设E是曲线C上的一点，且E到D的距离等于4，求E的坐标.

（2）设A、B是曲线C上横坐标不等于1的两个不同动点，直线PA、PB与y轴分别交于M、N两点，线段MN的垂直平分线经过P.证明：直线AB的斜率为定值.

（二）选考题：

22.    （10分）

在平面直角坐标系中，曲线的参数方程为（α为参数），曲线的参数方程为（β为参数），射线与曲线交于A，射线与曲线交于点B，以原点为极点，x轴正半轴为极轴建立极坐标系.

（1）直接写出曲线、射线的极坐标方程；

（2）求△AOB的面积.

23.    （10分）

已知的最小值为m.

（1）求m

（2）若都为正实数，且a+b=m,求证：