


数学七年级下册2 用关系式表示的变量间关系精品ppt课件
展开
这是一份数学七年级下册2 用关系式表示的变量间关系精品ppt课件,共26页。PPT课件主要包含了学习目标,情境导入,三角形的底和高,探究新知,y3x,三角形底边长,三角形面积,归纳总结,随堂练习,y=025x+1等内容,欢迎下载使用。
1.能根据具体情景,用关系式表示变量间的关系, 根据关系式解决相关问题;2.并会根据关系式求值,初步体会自变量和因变量 的数值对应关系;3.通过动手实践与探索,让学生参与变量的发现和 函数概念的形成过程,提高分析问题和解决问题 的能力.
常量、变量、自变量、因变量:
2.在某一变化过程中,不断变化的量叫作变量.
3.如果一个变量y随另一个变量x的变化而变化,则把x叫作自变量 ,y叫作因变量.
1.在变化过程中数值始终不变的量叫做常量.
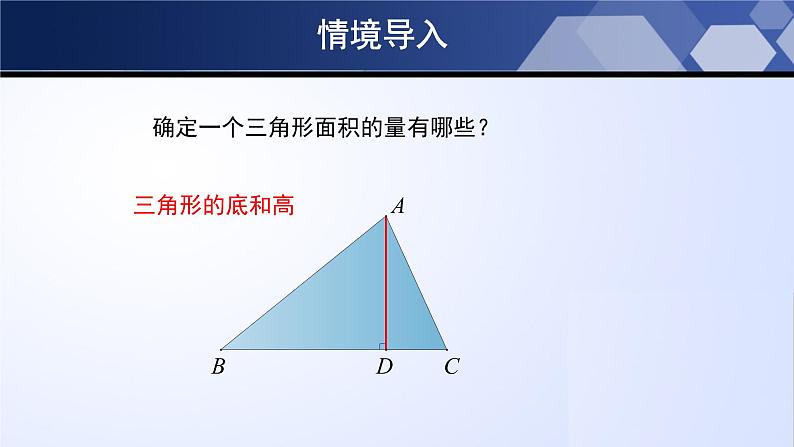
确定一个三角形面积的量有哪些?
用关系式表示变量间的关系
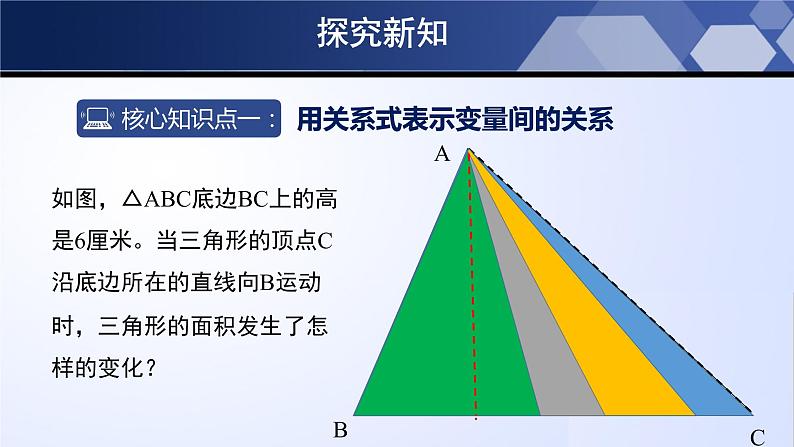
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
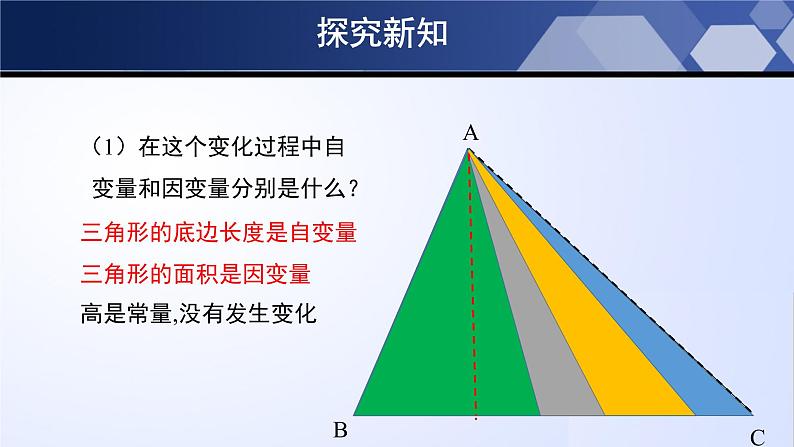
(1)在这个变化过程中自 变量和因变量分别是什么?三角形的底边长度是自变量三角形的面积是因变量高是常量,没有发生变化
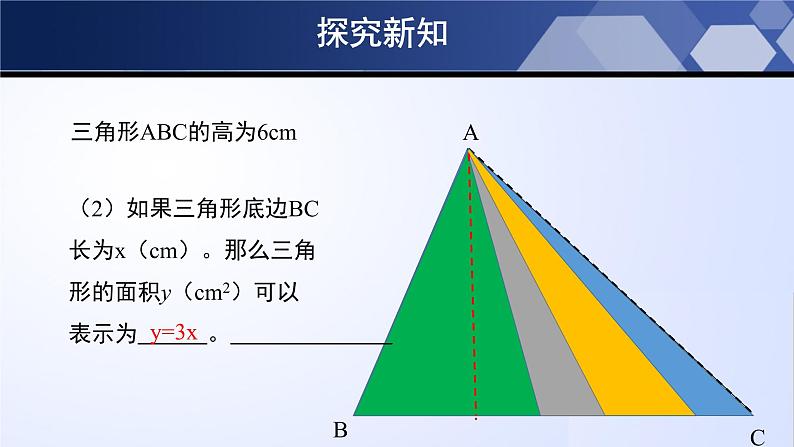
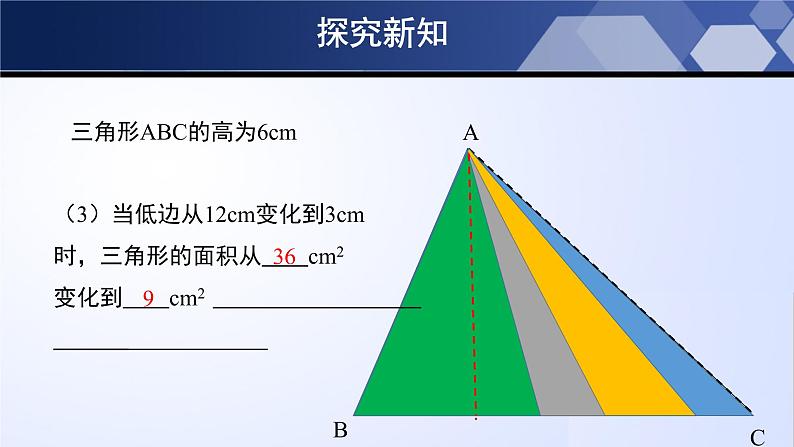
三角形ABC的高为6cm
(2)如果三角形底边BC长为x(cm)。那么三角形的面积y(cm2)可以表示为 。
(3)当低边从12cm变化到3cm时,三角形的面积从 cm2 变化到 cm2
y=3x表示了 和 之间的关系,它是变量y随x变化的关系式。
关系式是我们表示变量之间关系的另一种方法.
你能直观地表示这个关系式吗?
注意:关系式是一个等式;通常把因变量写在等号的左边,含有自变量的代数式写在等号的右边。
利用关系式,如y=3x ,可以根据任何一个符合条件的自变量的值求出因变量的值。
例1、△ABC的底边BC=10 cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.(1)在这个变化过程中,自变量和因变量各是什么?(2)△ABC的面积S(cm2)与高h(cm)之间的关系式是什么?(3)用表格表示当h由4cm变到10cm时(每次增加1cm),S的相应值.(4)当h每增加1cm时,S如何变化?
例1、△ABC的底边BC=10 cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.(1)在这个变化过程中,自变量和因变量各是什么?(2)△ABC的面积S(cm2)与高h(cm)之间的关系式是什么?
解:因为△ABC的面积随着高的变化而变化,所以高AD是自变量,△ABC的面积是因变量.
例1、△ABC的底边BC=10 cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.(3)用表格表示当h由4cm变到10cm时(每次增加1cm),S的相应值.(4)当h每增加1cm时,S如何变化?
解:当h由4cm变到10cm时,对应的S值如图所示:
解:根据(3)图表就可以得到当h每增加1cm时,S增加5cm2.
例2、如图,圆柱的底面直径是2cm,当圆柱的高h cm由大到小变化时,圆柱的体积V(cm3)随之发生变化.(1)在这个变化中,自变量和因变量各是什么?(2)写出圆柱的体积V与高h之间的关系式.(3)当h由10cm变化到5cm时,V是怎样变化的?(4)当h=0时,V等于多少?此时表示什么?
解:(1)自变量是圆柱的高,因变量是圆柱的体积.(2)V=πh.(3)当h=10cm时,V=πh=10πcm3;当h=5cm时,V=πh=5πcm3.所以当h由10cm变化到5cm时,V从10πcm3变化到5πcm3.(4)V=0,此时表示平面图形——直径为2cm的圆.
1. 汽车在匀速行驶过程中,路程s、速度v和时间t之间的关系为s=vt,下列说法正确的是( )A. s,v,t都是变量B. s,t是变量,v是常量C. v,t是变量,s是常量D. s,v是变量,t是常量
2. 在公式S=-t+20中,关于变量和常量,下列说法正确的是( )A. -1和20是常量,S和t是变量B. 20是常量,S和t是变量C. -1常量,S和t是变量D. S是自变量,t是因变量
4. 一只纸箱质量为1 kg,当放入一些苹果(每个苹果的质量为0.25 kg)后,纸箱和苹果的总质量不超过10 kg.(1)填表:
(2)设苹果数是x个,纸箱和苹果总质量为y kg,则y与x的关系式是______________________;
4. 一只纸箱质量为1 kg,当放入一些苹果(每个苹果的质量为0.25 kg)后,纸箱和苹果的总质量不超过10 kg.(3)请估计这只纸箱内最多能装多少个苹果.
解:设这只纸箱内装了m个苹果. 根据题意,得0.25m+1=10.解得m=36.所以苹果数的最大值是36.答:估计这只纸箱内最多能装36个苹果.
5. 如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
(1)上述两个变量之间的关系中,哪个是自变量?哪个是因变量?(2)用h(cm)表示这摞碗的高度,用x(只)表示这摞碗的数量,请用含有x的关系式表示h;(3)若这摞碗的高度为11.2 cm,求碗的数量.
解:(1)碗的数量是自变量,碗的高度是因变量.
(2)由表格中两个变量的变化关系,得h=4+1.2(x-1)=1.2x+2.8.
(3)当h=11.2时,得1.2x+2.8=11.2.解得x=7.答:若这摞碗的高度为11.2 cm,则碗的数量为7只.
6. 用100 m长的篱笆在地上围成一个矩形,当矩形的宽由小到大变化时,矩形的面积也随之发生变化. (1)在这个变化过程中,自变量、因变量各是什么?(2)设矩形的宽为x(m),求矩形的面积y(m2)与x的关系式;(3)当矩形的宽由1 m变化到25 m时,矩形面积由y1(m2)变化到y2(m2),求y1和y2的值.
解:(1)在这个变化过程中,自变量是矩形的宽,因变量是矩形的面积.
(3)当x=1时,y1=-12+50×1=49;当x=25时,y2=-252+50×25=625.
相关课件
这是一份数学七年级下册2 用关系式表示的变量间关系优质ppt课件,文件包含32用关系式表示的变量间关系课件pptx、32用关系式表示的变量间关系教案doc等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
这是一份初中数学北师大版七年级下册2 用关系式表示的变量间关系一等奖ppt课件,文件包含32用关系式表示的变量间关系pptx、北师大版中学数学七年级下第三章变量之间的关系32用关系式表示的变量间关系教学详案docx、32用关系式表示的变量间关系同步练习docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
这是一份初中数学北师大版七年级下册2 用关系式表示的变量间关系优秀课件ppt,共20页。PPT课件主要包含了太阳钟计时方法,你知道其中的道理吗,y3x,自变量x,因变量y,y0785x,785kg,5kg,y2x+100,2关系式等内容,欢迎下载使用。









