江苏省宿迁市崇文初级中学2022--2023学年七年级下学期3月月考数学试卷（含答案）

2022- 2023学年度第二学期第一次学情调研

初一数学试卷

本卷满分: 150 分考试时间:120分钟

班级:          姓名:         

一、选择题(本大题共8小题，每小题3分,共24分，在所给出的四个选项中，有且仅

有一项是符合题目要求的，请将正确选项的字母代号填写在答题纸相应位置上)

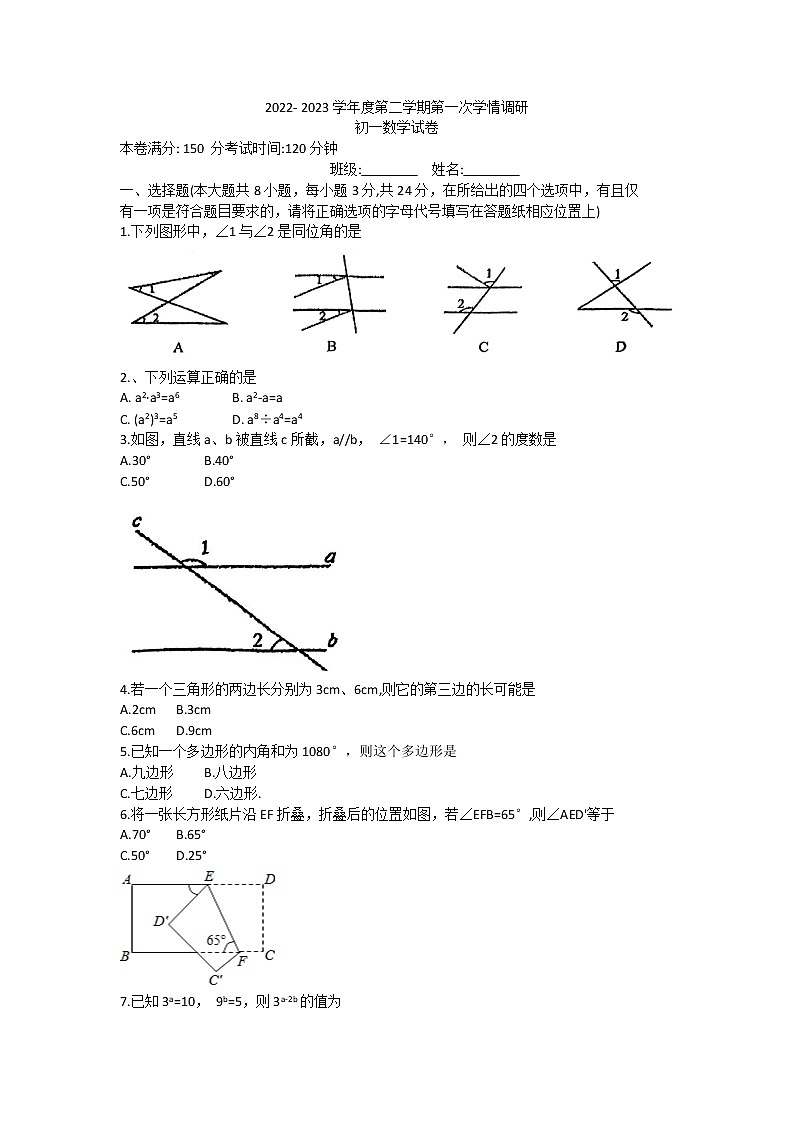
1.下列图形中，∠1与∠2是同位角的是

2.、下列运算正确的是

A. a2·a3=a6  B. a2-a=a

C. (a2)3=a5  D. a8÷a4=a4

3.如图，直线a、b被直线c所截，a//b， ∠1=140°， 则∠2的度数是

A.30°  B.40°

C.50°  D.60°

4.若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是

A.2cm B.3cm

C.6cm D.9cm

5.已知一个多边形的内角和为1080°，则这个多边形是

A.九边形  B.八边形

C.七边形  D.六边形.

6.将一张长方形纸片沿EF折叠，折叠后的位置如图，若∠EFB=65°,则∠AED'等于

A.70° B.65°

C.50° D.25°

7.已知3a=10， 9b=5，则3a-2b的值为

A.5  B.

C.  D.2

8.如图,将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边

重合，含30°角的直角三角板的斜边与纸条-边重合，含45°角的三角板的一个顶点在

纸条的另一边上，则∠1的度数是

A.15° B.22.5°

C.30° D.45°

二、填空题(本大题共10小题，每小题3分，共30分.不需写出解答过程，请把答案直

接填写在答题卡相应位贸上)

9.计算: (2a)2=       .

10.一个多边形的每一个内角都是120°， 则这个多边形是     边形.

11.若am=3，an=4，则am+n=      .

12.如图，AD是△ABC的中线，若△ABD的周长比△ACD的周长多6cm， 则AB-AC=       cm.

13.如图，在△ABC中，AD⊥BC, AE平分∠BAC,若∠l=30°,∠2=20°，则∠B=       °.

14. 82024x(-0.125)2023=     .

15.如图，∠1、∠2、∠3、∠4是五边形ABCDE的4个外角，∠A=110°,则∠1+∠2

+∠3+∠4=     °.

16. 如图，∠A+∠B+∠C+∠D+∠E+ CF的值是    °.

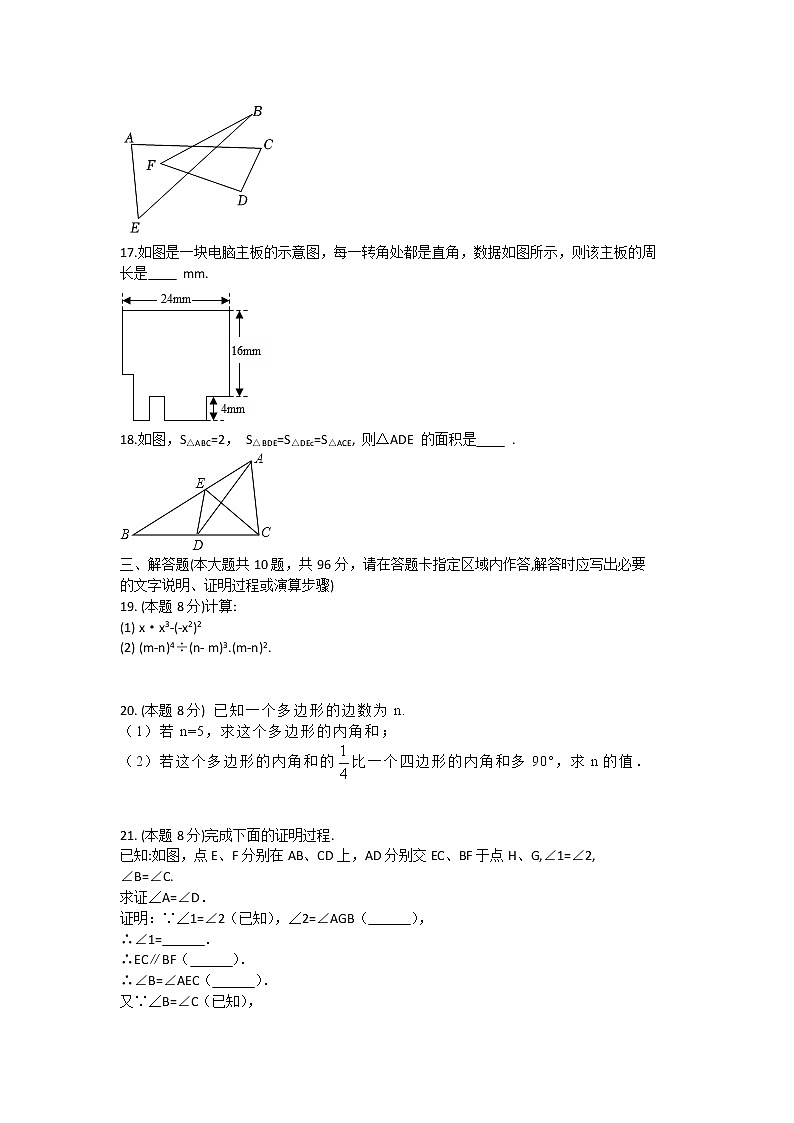
17.如图是一块电脑主板的示意图，每一转角处都是直角，数据如图所示，则该主板的周

长是     mm.

18.如图，S△ABC=2， S△BDE=S△DEc=S△ACE, 则△ADE 的面积是     .

三、解答题(本大题共10题，共96分，请在答题卡指定区域内作答,解答时应写出必要

的文字说明、证明过程或演算步骤)

19. (本题8分)计算:

(1) x·x3-(-x2)2

(2) (m-n)4÷(n- m)3.(m-n)2.

20. (本题8分) 已知一个多边形的边数为n.
（1）若n=5，求这个多边形的内角和；
（2）若这个多边形的内角和的比一个四边形的内角和多90°，求n的值．

21. (本题8分)完成下面的证明过程.

已知:如图，点E、F分别在AB、CD上，AD分别交EC、BF于点H、G,∠1=∠2,

∠B=∠C.

求证∠A=∠D．

证明：∵∠1=∠2（已知），∠2=∠AGB（      ），

∴∠1=      ．

∴EC∥BF（      ）．

∴∠B=∠AEC（      ）．

又∵∠B=∠C（已知），

∴∠AEC=       ．

∴      （      ）．

∴∠A=∠D（       ）．

22.(本题8分)如图，△4BC的顶点都在方格纸的格点上,将△ABC向左平移2格，再向上平移3格，其中每个格子的边长为1个单位长度.

(1)画出△ABC边AB上的高CD;

(2)请在图中画出平移后的三角形A'B'C';

(3)若连接BB', CC'，则这两条线段之间的关系是       ．

23.(10分)如图，已知AB∥CD，∠1=∠2，CF平分∠DCE．
（1）试判断直线AE与BF有怎样的位置关系？并说明理由；
（2）若∠1=80°，求∠3的度数．

24. (本题 10分) 若am=an（a＞0且a≠1，m,n是正整数），则m=n,利用上面结论解决下面的问题：
（1）如果4x×8x=25，求x的值；

（2）如果3x×2x+1+2x×3x+1=180，求x的值．

25. (本题10分)如图，CE是△ABC的外角∠ACD的平分线,

且CE交BA的延长线于点E..

(1)若∠B=35°， ∠E= =25°， 求∠CAE的度数;

(2)试说明:∠BAC=∠B+2∠E.

26. (本题10分)如图，已知∠l=∠BCE，∠2+ ∠3= 180°,

(1)判断AC与EF的位置关系，并说明理由;

(2)若CA平分∠BCE，EF⊥AB交BA的延长线于点F,

∠1=72°，求C BAD的度数.

27. (本题12分) 规定两数a,b之间的一种运算，记作（a,b），如果am=b,则（a,b）=m.我们叫（a,b）为“雅对”．例如：因为23=8，所以（2，8）=3．我们还可以利用“雅对”定义说明等式（3，3）+（3，5）=（3，15）成立．证明如下：
设（3，3）=m,（3，5）=n,则3m=3，3n=5，故3m•3n=3m+n=3×5=15，则（3，15）=m+n,即（3，3）+（3，5）=（3，15）．
（1）根据上述规定，填空：（5，125）=    ；（     ，16）=4；
（2）计算（5，2）+（5，7）=    ，并说明理由；
（3）利用“雅对”定义说明：（2n，3n）=（2，3） (n是正整数)．

28. (本题 12分)如图，四边形ABCD, BE、DF分别平分四边形的外角∠MBC和∠NDC,

若∠BAD=a,∠BCD=β. .

(1)如图1,若a+p= 105°，求∠MBC+∠NDC的度数;

(2)如图1,若BE与DF相交于点G,∠BGD=45°,请直接写出a, β的数量关系式;

(3)如图2,若a=β,判断BE, DF的位置关系，并说明理由.

参考答案

1.C  2. D  3. B  4. C  5. B  6. C  7. D  8. A 

9.4 a2  10.六  11.12  12.6  13.50  14.- 8  15.290  16.360  17.96  18.

19．(1) x·x3-(-x2)2

=x4-x4=0

(2) (m-n)4÷(n- m)3.(m-n)2.

=(m-n)4-3+2=(m-n)3

20. （1）当n=5时，（5-2）×180°=540°．                               （
∴这个多边形的内角和为540°．
（2）由题意，得×（n−2）×180°−360°=90°，
解得n=12．
∴n的值为12．

21．证明：∵∠1=∠2（已知），
∠2=∠AGB（对顶角相等），
∴∠1=∠AGB．
∴EC∥BF（同位角相等，两直线平行）．
∴∠B=∠AEC（两直线平行，同位角相等）．
又∵∠B=∠C（已知），
∴∠AEC=∠C．
∴AB∥CD（内错角相等，两直线平行）．
∴∠A=∠D（两直线平行，内错角相等）．
故答案为：对顶角相等；∠AGB；同位角相等，两直线平行；两直线平行，同位角相等；∠C；AB∥CD；内错角相等，两直线平行；两直线平行，内错角相等．

22. （1）如图所示，线段CD即为所求；

（2）如图所示，△A'B'C′即为所求，△A'B'C′的面积为×4×4=8；
（3）由平移变换的性质知BB'，CC′这两条线段之间的关系是平行且相等，
故答案为：平行且相等．

23．（1）AC∥BD．理由如下：
∵AB∥CD，
∴∠2=∠CDF，
∵∠1=∠2，
∴∠1=∠CDF，
∴AE∥BF；
（2）∵∠1=80°，
∴∠ECD=180°-∠1=180°-80°=100°，
∵CF平分∠ECD，
∴∠ECF=∠ECD=50°．
∵AC∥BD，
∴∠3=∠ECF=50°．

24. （1）4x×8x=25，所以2x+3x=5，解得x=1.

（2）∵3x×2x+1+2x×3x+1=180，
∴3x×2x×2+2x×3x×3=180，
∴3x2x（2+3）=22×32×5，
∴3x×2x×5=32×22×5，
∴x=2．

25．（1）解：∵∠DCE是△BCE的外角，∠B=35°，∠E=25°，
∴∠DCE=∠B+∠E=60°，
∵CE平分∠ACD，
∴∠ACE=∠DCE=60°，
∴∠CAE=180°-∠ACE-∠E=95°；
（2）证明：∵∠DCE是△BCE的外角，∠BAC是△ACE的外角，
∴∠DCE=∠B+∠E，∠BAC=∠E+∠ACE，
∵CE平分角ACD，
∴∠ACE=∠DCE，
∴∠BAC=∠E+∠B+∠E=∠B+2∠E．

26．（1）AC∥EF．理由：
∵∠1=∠BCE，
∴AD∥CE．
∴∠2=∠4．
∵∠2+∠3=180°，
∴∠4+∠3=180°．
∴EF∥AC．
（2）∵AD∥EC，CA平分∠BCE，
∴∠ACD=∠4=∠2．
∵∠1=72°，
∴∠2=36°．
∵EF∥AC，EF⊥AB于F，
∴∠BAC=∠F=90°．
∴∠BAD=∠BAC-∠2
=54°．

27．（1）∵53=125，
∴（5，125）=3；
∵（±2）4=16，
∴（±2，16）=4；
故答案为：3，±2；
（2）（5，2）+（5，7）=（5，14）；
理由如下：
设（5，2）=m,（5，7）=n,则5m=2，5n=7，
∴5m•5n=5m+n=2×7=14，
∵（5，14）=m+n,
∴（5，2）+（5，7）=（5，14）；
故答案为：（5，14）；
（3）设（2n，3n）=a,（2，3）=b,
∴（2n）a=3n，2b=3，
∴（2n）a=（2b）n，
即2an=2bn，
∴an=bn,
∴a=b,
即（2n，3n）=（2，3），对于任意自然数n都成立．

28. （1）∵四边形ABCD的内角和为360°，
∴α+β=∠A+∠BCD=360°-（∠ABC+∠ADC），
∵∠MBC和∠NDC是四边形ABCD的外角，
∴∠MBC=180°-∠ABC，∠NDC=180°-∠ADC，
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC
=360°-（∠ABC+∠ADC），
=α+β
=105°；
（2）β-α=90°（或α-β=-90°等均正确）．
理由：如图1，连接BD，

由（1）有，∠MBC+∠NDC=α+β，
∵BE、DF分别平分四边形的外角∠MBC和∠NDC，
∴∠CBG=∠MBC，∠CDG=∠NDC，
∴∠CBG+∠CDG=∠MBC+∠NDC=（∠MBC+∠NDC）=（α+β），
在△BCD中，∠BDC+∠CBD=180°-∠BCD=180°-β，
在△BDG中，∠BGD=45°，∠GBD+∠GDB+∠BGD=180°，
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°，
∴（∠CBG+∠CDG）+（∠BDC+∠CBD）+∠BGD=180°，
∴（α+β）+180°-β+45°=180°，
∴β-α=90°．
（3）BE∥DF．
理由：如图2，过点C作CP∥BE，

则∠EBC=∠BCP，
∴∠DCP=∠BCD-∠BCP=β-∠EBC，
由（1）知∠MBC+∠NDC=α+β，
∵α=β，
∴∠MBC+∠NDC=2β，
又∵BE、DF分别平分∠MBC和∠NDC，
∴∠EBC+∠FDC=（∠MBC+∠NDC）=β，
∴∠FDC=β-∠EBC，
又∵∠DCP=β-∠EBC，
∴∠FDC=∠DCP，
∴CP∥DF，
又CP∥BE，
∴BE∥DF．