新高考数学一轮复习课件 第2章 §2.2　函数的单调性与最值

这是一份新高考数学一轮复习课件 第2章 §2.2　函数的单调性与最值，共60页。PPT课件主要包含了落实主干知识，探究核心题型，课时精练等内容，欢迎下载使用。
§2.2　函数的单调性与最值
1.借助函数图象，会用数学符号语言表达函数的单调性、最值，理解实际意义.2.掌握函数单调性的简单应用.
LUOSHIZHUGANZHISHI
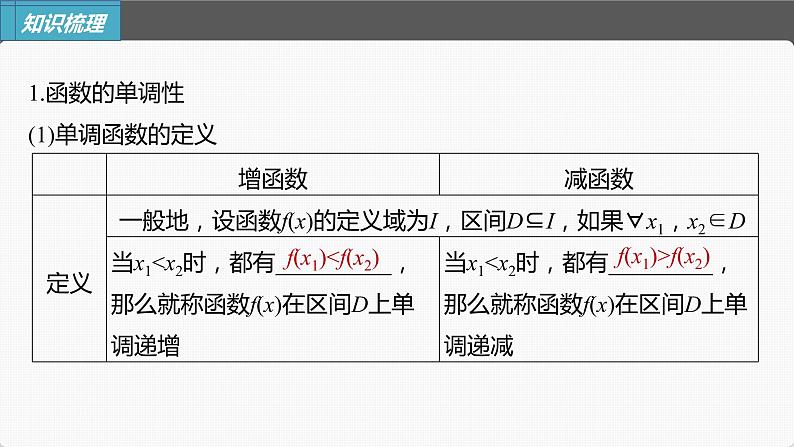
1.函数的单调性(1)单调函数的定义
f(x1)f(x2)
(2)单调区间的定义如果函数y＝f(x)在区间D上_________或_________，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间D叫做y＝f(x)的单调区间.
2.在公共定义域内，增函数＋增函数＝增函数，减函数＋减函数＝减函数.
4.复合函数的单调性：函数y＝f(u)，u＝φ(x)在函数y＝f(φ(x))的定义域上，如果y＝f(u)与u＝φ(x)的单调性相同，那么y＝f(φ(x))单调递增；如果y＝f(u)与u＝φ(x)的单调性相反，那么y＝f(φ(x))单调递减.
判断下列结论是否正确(请在括号中打“√”或“×”)(1)若f(x)的定义域为R，且f(－3)f(b)
y＝ex是增函数，y＝e－x是减函数，因此在(0，＋∞)上y＝ex－e－x单调递增，且此时f(x)>0.f(x)＝－x2在x≤0时单调递增，所以f(x)在R上单调递增.c＝lg20.9c，所以f(a)>f(b)>f(c).
5.(多选)已知函数f(x)＝x－ (a≠0)，下列说法正确的是A.当a>0时，f(x)在定义域上单调递增B.当a＝－4时，f(x)的单调递增区间为(－∞，－2)，(2，＋∞)C.当a＝－4时，f(x)的值域为(－∞，－4]∪[4，＋∞)D.当a>0时，f(x)的值域为R
定义域为(－∞，0)∪(0，＋∞).∵f(x)在(－∞，0)，(0，＋∞)上单调递增，故A错误；又x→－∞时，f(x)→－∞，x→0－时，f(x)→＋∞，∴f(x)的值域为R，故D正确；
由其图象(图略)可知，B，C正确.
6.(多选)已知函数f(x)＝ 则下列结论正确的是A.f(x)在R上为增函数B.f(e)>f(2)C.若f(x)在(a，a＋1)上单调递增，则a≤－1或a≥0D.当x∈[－1,1]时，f(x)的值域为[1,2]
易知f(x)在(－∞，0]，(0，＋∞)上单调递增，A错误，B正确；若f(x)在(a，a＋1)上单调递增，则a≥0或a＋1≤0，即a≤－1或a≥0，故C正确；当x∈[－1,0]时，f(x)∈[1,2]，当x∈(0,1]时，f(x)∈(－∞，2]，故x∈[－1,1]时，f(x)∈(－∞，2]，故D不正确.
7.函数y＝－x2＋2|x|＋1的单调递增区间为_________________，单调递减区间为_________________.
(－∞，－1]和[0,1]
(－1,0)和(1，＋∞)
画出函数的图象如图所示，单调递增区间为(－∞，－1]和[0,1]，单调递减区间为(－1,0)和(1，＋∞).
8.(2022·山东师大附中质检)已知函数f(x)＝e|x－a|(a为常数)，若f(x)在区间[1，＋∞)上单调递增，则实数a的取值范围是_________.
当x≥a时，f(x)单调递增，当x0)，且f(x)在(0,1]上的最大值为g(a)，求g(a)的最小值.
∴f(x)在(0,1]上单调递增，
∴g(a)的最小值为2.
10.已知函数f(x)＝a－ .(1)求f(0)；
(2)探究f(x)的单调性，并证明你的结论；
f(x)在R上单调递增．证明如下：∵f(x)的定义域为R，∴任取x1，x2∈R且x1