泰山区泰山实验中学2023年八年级第二学期第九章图形的相似单元检测题和答案

八年级数学下册第9章  图形的相似检测题

（满分120分  90分钟）

班级                      姓名                    成绩                  

一、选择题(每小题3分,共36分)

1.若=，则的值为（　　）

A．1          B．             C．              D．

2.已知线段a、b、c，其中c是a、b的比例中项，若a=9cm，b=4cm，则线段c长（　　）

A．18cm          B．5cm             C．6cm              D．±6cm

3.已知点P是线段AB的黄金分割点（AP＞PB），AB=4，那么AP的长是（　　）

A．      B．         C．          D．

4．如图，∠ACB=∠ADC=90°，BC=a,AC=b,AB=c，要使⊿ABC∽⊿CAD，只要CD等于（     ）

A．      B．       C．       D．

5．如果两个相似三角形的面积比是1：4，那么它们的周长比是（　　）

A．1：16      B．1：4          C．1：6          D．1：2

6．如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（　　）

 A．  4          B．  7              C．  3              D．  12

7．如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD若B（1，0），则点C的坐标为（　　）

A．（1，2）       B．（1，1）     C．（，）       D．（2，1）

8．如图，已知△ABC和△ADE均为等边三角形，D在BC上，DE与AC相交于点F，AB=9，BD=3，则CF等于(　　）

 A．1             B．2              C．3               D．4

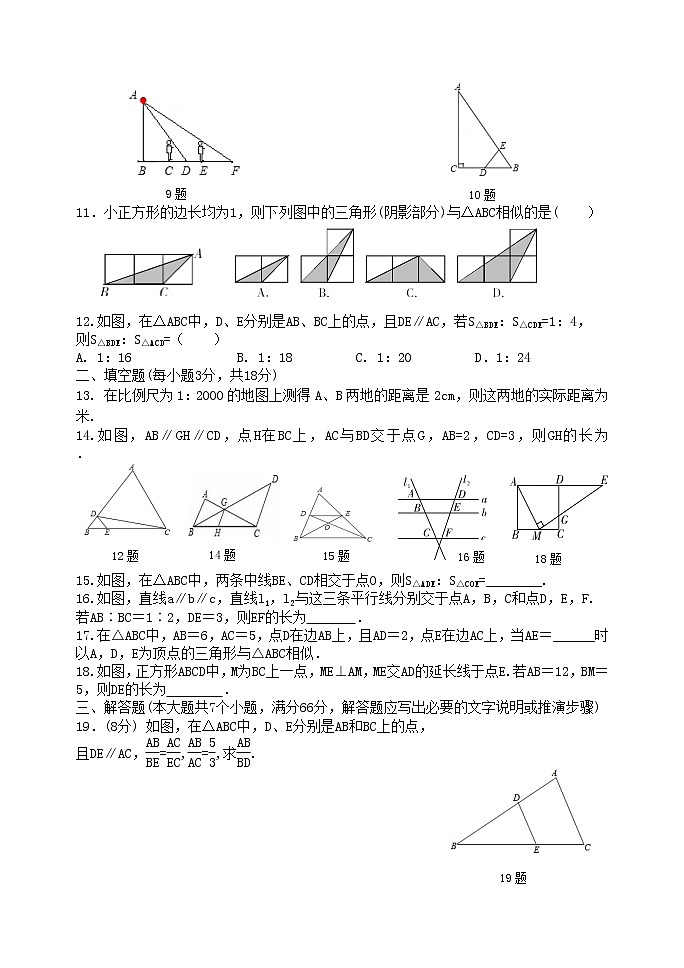
9．如图，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，继续往前走3米到达E处时，测得影子EF的长为2米,王华的身高是1.5米，则路灯A的高度AB等于（　　）

A．4.5米      B．6米       C．7.2米          D．8米

10．如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE当△BDE是直角三角形时，t的值为（　　）

A．2        B．2.5或3.5          C．3.5或4.5         D．2或3.5或4.5

11．小正方形的边长均为1，则下列图中的三角形(阴影部分)与△ABC相似的是(　　）

12.如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若S△BDE：S△CDE=1：4，

则S△BDE：S△ACD=（　　）

A. 1：16               B. 1：18         C. 1：20         D．1：24     

二、填空题(每小题3分，共18分)

13. 在比例尺为1：2000的地图上测得A、B两地的距离是2cm，则这两地的实际距离为       米.

14.如图，AB∥GH∥CD，点H在BC上，AC与BD交于点G，AB=2，CD=3，则GH的长为       ．

15.如图，在△ABC中，两条中线BE、CD相交于点O，则S△ADE：S△COE=________.

16.如图，直线a∥b∥c，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F.

若AB∶BC＝1∶2，DE＝3，则EF的长为       ．

17.在△ABC中，AB＝6，AC＝5，点D在边AB上，且AD＝2，点E在边AC上，当AE＝______时以A，D，E为顶点的三角形与△ABC相似．

18.如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交AD的延长线于点E.若AB＝12，BM＝5，则DE的长为        ．

三、解答题(本大题共7个小题，满分66分，解答题应写出必要的文字说明或推演步骤)

19．(8分) 如图，在△ABC中，D、E分别是AB和BC上的点，

且DE∥AC，=,=,求.

20．(8分)如图，在ΔABC中，EF//DC，DE//BC，

求证：（1）AF︰FD＝AD︰DB； （2）AD2＝AF·AB.

21．(9分) 如图，在平行四边形ABCD中，对角线AC、BD交于点O．M为AD中点，连接CM交BD于点N，且ON=1．

（1）求BD的长；

（2）若△DCN的面积为2，求四边形ABNM的面积．

22．(10分) 如图，有一块三角形铁片ABC ，BC=12 cm，高AD=8 cm，要把它加工成一个矩形铁片，使矩形的长边在BC上，其余两个顶点分别在AB ，AC上，且要求矩形的长QN是宽QP的2倍.

(1)求加工成的矩形铁片的长与宽.  

(2)求ΔANQ的面积.

23．(10分) 如图，在同一时刻两根木竿在太阳光下的影子如图所示 ，其中木竿AB= 2m，它的影子BC=1.6m，木竿PQ的影子有一部分落在了墙上， PM= 1.2m，MN=0.8m，求木竿PQ的长度.

24．(10分) 如图， P 是正方形 ABCD 边 BC 上的一点，且BP = 3PC，Q 是 CD 中点.

（1） 求证：ΔADQ ∽ΔQC P.

（2）试问：AQ 与 PQ有什么关系（位置与数量）?

25．(12分) 在四边形中，平分，，为的中点.

(1)求证: AC2=AD·AB

(2)求证:CE∥AD.

(3)若AD=4，AB=6，求的值.

第9章  图形的相似检测题答案      

一、选择题

1.D     2.C     3.A      4.A      5.D      6.B      7.B      8.B      9.B

10.D    11.A    12.C

二、填空题(每小题3分，共18分)

13.40   14.65    15.3:2   16.6     17.125或53      18.1095

三、解答题(本大题共7个小题，满分66分，解答题应写出必要的文字说明或推演步骤)

19．解：∵ABBE=ACEC，

∴ABAC=BEEC=53，

∵DE∥AC，

∴ADBD=ECBE=35，

∴ABBD=AD+BDBD=ADBD+1=35+1=85

20．证明：(1)∵EF∥DC,DE∥BC，

∴AF:FD=AE:EC，AD:DB=AE:EC，

∴AF:FD=AD:DB；

(2)∵EF∥DC,DE∥BC，

∴△AFE∽△ADC,△ADE∽△ABC，

∴AF:AD=AE:AC，AD:AB=AE:AC，

∴AF:AD=AD:AB，

∴AD2=AF⋅AB.

21．(1)∵平行四边形ABCD，

∴AD∥BC，AD=BC，OB=OD，

∴∠DMN=∠BCN，∠MDN=∠NBC，

∴△MND∽△CNB，

∴MDCB=DNBN，

∵M为AD中点，

∴MD=12AD=12BC,即MDCB=12，

∴DNBN=12，即BN=2DN，

设OB=OD=x，则有BD=2x，BN=OB+ON=x+1，DN=x−1，

∴x+1=2(x−1)，

解得：x=3，

∴BD=2x=6；

 (2)∵△MND∽△CNB，且相似比为1:2，

∴MN:CN=DN:BN=1:2，

∴S△MND=12S△CND=1,S△BNC=2S△CND=4.

∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6

∴S四边形ABNM=S△ABD−S△MND=6−1=5.

22．(1)记AD与QN的交点为E.

∵四边形QPMN是矩形，

∴QN∥PM，

∴△AQN∽△ABC.

∵AD⊥BC，

∴AD是BC边上的高.

∵AE⊥QN，

∴AE是QN边上的高线，

∴AEAD=QNBC.

设矩形QPMN的宽PQ=xcm，则矩形的长QN=2xcm.

∵AD=AE+ED，ED=PQ=x，AD=8cm，

∴AE=(8-x)cm.

∵AD=8cm，AE=（8-x）cm，BC=12cm，QN=2xcm，AEAD=QNBC，

∴8−x8=2x12，

∴x=247，

∴长为487，宽为247.

(2)S△ANQ=12·AE·QN=12·(8-247)·487=76849cm2

23．过N点作ND⊥PQ于D，

∴BCAB=DNQD，

又∵AB=2m，BC=1.6m，PM=1.2m，NM=0.8m，

∴QD=AB⋅DNBC=1.5m，

∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(m).

答：木竿PQ的长度为2.3米.

24．(1)证明：∵四边形ABCD是正方形，

∴AD=CD,∠C=∠D=90∘；

又∵Q是CD中点，

∴CQ=DQ=12AD；

∵BP=3PC，

∴CP=14AD，

∴CQAD=CPDQ=12，

又∵∠C=∠D=90∘，

∴△ADQ∽△QCP；

 (2)AQ=2PQ，且AQ⊥PQ.理由如下：

由(1)知,△ADQ∽△QCP, CQAD=CPDQ=12，

则AQQP=CQAD=CPDQ=12，

AQ=2PQ；

∵△ADQ∽△QCP，

∴∠AQD=∠QPC，∠DAQ=∠PQC，

∴∠PQC+∠DQA=DAQ+AQD=90∘，

∴AQ⊥QP.

25．(1)证明：∵AC平分∠DAB，

∴∠DAC=∠CAB，

∵∠ADC=∠ACB=90∘，

∴△ADC∽△ACB，

∴AD:AC=AC:AB，

∴AC2=AB⋅AD；

(2)∵∠ACB=90∘，E为AB中点，

∴AE=CE，

∴∠CAE=∠ECA，

∵AC平分∠DAB，

∴∠DAC=∠EAC，

∴∠DAC=∠ACE，

∴CE∥AD，

∴△AFD∽△CFE，

∴AD:CE=AF:CF，

∵CE=12AB，

∴CE=12×6=3，

∵AD=4，

∴43，

∴ACAF=74.