

深圳盐田高级中学2021-2022学年第二学期期中考试高二数学试卷
展开 2021-2022学年第二学期期中考试
盐田高级中学高二数学试卷
命题人:刘国华 审题人:康宇
考试时间:120分钟 满分:150分
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求.
1.已知等差数列的前n项和为.若,则( ).
A.60 B.50 C.30 D.20
2.下列有关样本相关系数说法错误的是( ).
A.,且越接近1,相关程度越大 B.,且越接近0,相关程度越小
C.,且越接近1,相关程度越大 D.相关系数用来衡量变量x与y的线性相关程度
3.若的展开式中的常数项为则( ).
A.2 B.-2 C.1 D.-1
4.袋中装有除颜色外其余均相同的10个红球,5个黑球,每次任取一球,若取到黑球,则放入袋中,直到取到红球为止.若抽取的次数为,则表示“放回4个球”的事件为( ).
A. B. C. D.
5.已知某地市场上供应的灯泡中,甲厂产品占70%,乙厂产品占30%,甲厂产品的合格率是90%,乙厂产品的合格率是80%,则从该地市场上买到一个合格灯泡的概率是( ).
A.0.63 B.0.24 C.0.87 D.0.21
6.《易系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这个数中任取个数,则这个数中至少有
个阳数的概率为( ).
A. B.
C. D.
7.设点是函数图像上的任意一点,点处切线的倾斜角为,则角的取值范围是( ).
A. B. C. D.
8.已知椭圆,其左右焦点分别为,其离心率为,点P为该椭圆上一点,且满足,已知的内切圆的面积为,则该椭圆的长轴长为( ).
A.2 B.4 C.6 D.12
二、多项选择题:本大题共4小题,每小题5分,共计20分.每小题给出的四个选项中,都有多个选项是正确的,全部选对的得5分,选对但不全的得2分,选错或不答的得0分.
9.若随机变量X服从两点分布,其中,则下列结论正确的是( ).
A. B. C. D.
10.若,则m的取值可能是( )
A.6 B.7 C.8 D.9
11.已知双曲线,则( ).
A.双曲线的焦点在轴上 B.双曲线的焦距等于
C.双曲线的焦点到其渐近线的距离等于 D.双曲线的离心率的取值范围为
12.已知a为常数,函数有两个极值点 (),则( ).
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.已知随机变量服从正态分布,,则________.
14.新年音乐会安排了2个唱歌、3个乐器和2个舞蹈共7个节目,则2个唱歌节目不相邻的节目单共有___________种.(用数字表示)
15.考察下列两个问题:①已知随机变量,且,,记;②甲、乙、丙三人随机到某3个景点去旅游,每人只去一个景点,设表示“甲、乙、丙所去的景点互不相同”,表示“有一个景点仅甲一人去旅游”,记,则 , .
16.用1,2,3,4,5组成没有重复数字的五位数,其中个位小于百位且百位小于万位的五位数有n个,则的展开式中,的系数是___________.(用数字作答)
四、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
17.等差数列前n项和为,且
(1)求数列的通项公式;
(2)设数列的前n项和为,若,求n的最小值.
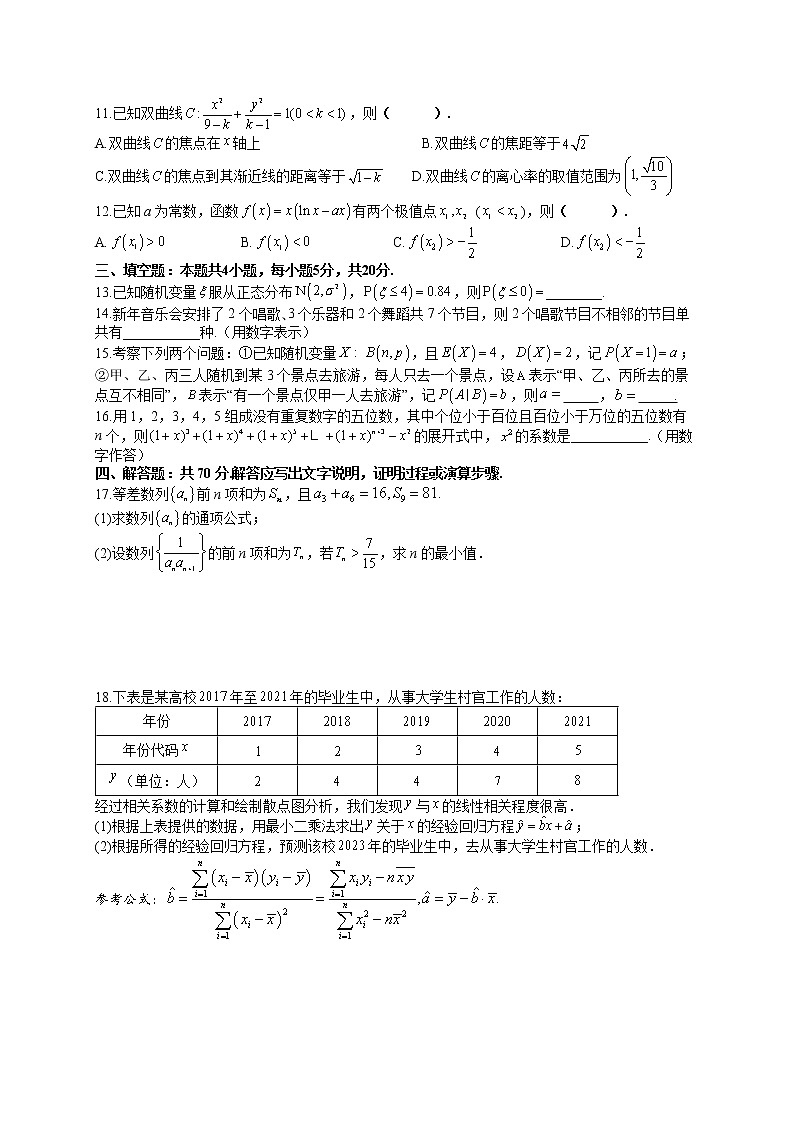
18.下表是某高校年至年的毕业生中,从事大学生村官工作的人数:
年份
年份代码
(单位:人)
经过相关系数的计算和绘制散点图分析,我们发现与的线性相关程度很高.
(1)根据上表提供的数据,用最小二乘法求出关于的经验回归方程;
(2)根据所得的经验回归方程,预测该校年的毕业生中,去从事大学生村官工作的人数.
参考公式:
19.某校在高一部分学生中调查男女同学对某项体育运动的喜好情况,其等高堆积条形图如图(黑色代表喜欢,白色代表不喜欢,单位:人).
(1)写出列联表;
(2)依据的独立性检验,分析喜欢这项体育运动是否与性别有关;
(3)在这次调查中,从喜欢这项体育运动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
附表及公式:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
,其中.
20.深圳市某高中学校组织航天科普知识竞赛,分小组进行知识问题竞答.甲乙两个小组分别从6个问题中随机抽取3个问题进行回答,答对题目多者为胜.已知这6个问题中,甲组能正确回答其中4个问题,而乙组能正确回答每个问题的概率均为.甲、乙两个小组的选题以及对每题的回答都是相互独立,互不影响的.
(1)求甲小组至少答对2个问题的概率;
(2)若从甲乙两个小组中选拔一组代表学校参加全市决赛,请分析说明选择哪个小组更好?
21.已知抛物线的焦点为F,过F的直线与抛物线C交于A,B两点,当A,B两点的纵坐标相同时,.
(1)求抛物线C的方程;
(2)若P,Q为抛物线C上两个动点,,E为PQ的中点,求点E纵坐标的最小值.
22.已知函数
(1)当时,求函数的单调区间;
(2)若,正实数满足,求证:
2021-2022学年第二学期期中考试
盐田高级中学高二数学试卷解析
1-8 CADBC CBD 9-12(AB)(BC)(ACD)(BC)
13.; 14. 3600; 15.; 16. 2022.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求.
1.已知等差数列的前n项和为.若,则( C ).
A.60 B.50 C.30 D.20
解析:.选C.
2.下列有关样本相关系数说法错误的是( A ).
A.,且越接近1,相关程度越大 B.,且越接近0,相关程度越小
C.,且越接近1,相关程度越大 D.相关系数用来衡量变量x与y的线性相关程度
解析:由相关系数的定义可得,A错;由相关系数的性质可得:当越接近0,相关程度越小,B对;越接近1,相关程度越大,C对;相关系数与x与y的线性相关程度有关,D对.选A.
3.若的展开式中的常数项为-20,则a=( D ).
A.2 B.-2 C.1 D.-1
解析:已知的展开式中的通项公式为:,令,求得,可得展开式的常数项为,解得.选D.
4.袋中装有除颜色外其余均相同的10个红球,5个黑球,每次任取一球,若取到黑球,则放入袋中,直到取到红球为止.若抽取的次数为,则表示“放回4个球”的事件为( B).
A. B. C. D.
解析:根据题意可知,若取到黑球,则将黑球放回,然后继续抽取,若取到红球,则停止抽取,所以“放回4个球”即前4次都是取到黑球,第5次取到了红球,故.选B.
5.已知某地市场上供应的灯泡中,甲厂产品占70%,乙厂产品占30%,甲厂产品的合格率是90%,乙厂产品的合格率是80%,则从该地市场上买到一个合格灯泡的概率是( C).
A.0.63 B.0.24 C.0.87 D.0.21
解析:从某地市场上购买一个灯泡,设买到的灯泡是甲厂产品为事件A,买到的灯泡是乙厂产品为事件B,则由题可知P(A)=0.7,P(B)=0.3.从甲厂产品中购买一个,设买到的产品是合格品为事件C,从乙厂产品中购买一个,设买到的产品是合格品为事件D,则由题可知P(C)=0.9,P(D)=0.8,由题可知A、B、C、D互相独立,故从该地市场上买到一个合格灯泡的概率为:
P(AC)+P(BD)=P(A)P(C)+P(B)P(D)=0.7×0.9+0.3×0.8=0.87.选C.
6.《易系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这个数中任取个数,则这个数中至少有
个阳数的概率为( C).
A. B.
C. D.
解析:由题意可知,个数中,、、、、是阳数,、、、、是阴数,
若任取个数中有个阳数,则,若任取个数中有个阳数,则,故这个数中至少有个阳数的概率,选C.
7.设点是函数图像上的任意一点,点处切线的倾斜角为,则角的取值范围是( B ).
A. B. C. D.
解析:,,,,,.点P是曲线上的任意一点,点P处切线的倾斜角为,.,.选B.
8.已知椭圆,其左右焦点分别为,其离心率为,点P为该椭圆上一点,且满足,已知的内切圆的面积为,则该椭圆的长轴长为( D ).
A.2 B.4 C.6 D.12
解析:由,得,即.设的内切圆的半径为,则因为的内切圆的面积为,所以,解得(负舍),在中,根据椭圆的定义及焦点三角形的面积公式,知,即,由,
联立,得,所以该椭圆的长轴长为.选D.
二、多项选择题:本大题共4小题,每小题5分,共计20分.每小题给出的四个选项中,都有多个选项是正确的,全部选对的得5分,选对但不全的得2分,选错或不答的得0分.
9.若随机变量X服从两点分布,其中,则下列结论正确的是( AB ).
A. B. C. D.
解析:∵随机变量X服从两点分布,其中,∴,∴,,故A正确,D错误; ,故B正确; ,故C错误.选AB.
10.若,则m的取值可能是( )
A.6 B.7 C.8 D.9
解析:根据题意,对于,有0≤m﹣1≤8且0≤m≤8,则有1≤m≤8,
若,则有,
变形可得:m>27﹣3m,解可得:m>,
综合可得:<m≤8,则m=7或8;故选:BC.
11.已知双曲线,则( ACD ).
A.双曲线的焦点在轴上 B.双曲线的焦距等于
C.双曲线的焦点到其渐近线的距离等于 D.双曲线的离心率的取值范围为
解析:对A:因为,所以,,所以双曲线表示焦点在轴上的双曲线,故选项A正确;对B:由A知,所以,所以,所以双曲线的焦距等于,
故选项B错误;对C:设焦点在轴上的双曲线的方程为,焦点坐标为,则渐近线方程为,即,所以焦点到渐近线的距离,
所以双曲线的焦点到其渐近线的距离等于,故选项C正确;
对D:双曲线的离心率,因为,所以,所以,故选项D正确.选ACD.
12.已知a为常数,函数有两个极值点则( BC ).
A. B. C. D.
解析:易得,依题意,知有两个不等实根
即函数的图像与函数的图像有两个不同交点,如图所示:
,设g(x)过原点的切线与g(x)相切于,
斜率为,故切线方程为:,
∵过原点,∴,解得=1,故切线斜率为1,切线方程为y=x,切点为.
则由图可知,,且,∴.由,得,故,当时,由图可知,g(x)>h(x),即,
∴f(x)此时单调递增,又,∴.选BC.
三、填空题:本题共4小题,每小题5分,共20分.
13.已知随机变量服从正态分布,,则________.
解析:因为随机变量服从正态分布,所以正态曲线的对称轴为.由及正态分布的性质,
14.新年音乐会安排了2个唱歌、3个乐器和2个舞蹈共7个节目,则2个唱歌节目不相邻的节目单共有___________种.(用数字表示)
解析:先排3个乐器和2个舞蹈共5个节目有种排法,其中有6个空插入2个唱歌节目,有种排法,故共有故答案为:3600.
15.考察下列两个问题:①已知随机变量,且,,记;②甲、乙、丙三人随机到某3个景点去旅游,每人只去一个景点,设表示“甲、乙、丙所去的景点互不相同”,表示“有一个景点仅甲一人去旅游”,记,则 , .
解析:问题①,由,解得,则.
问题②,根据题意,事件B的可能情况有种,事件发生的可能情况为种,所以,.即
16.用1,2,3,4,5组成没有重复数字的五位数,其中个位小于百位且百位小于万位的五位数有n个,则的展开式中,的系数是___________.(用数字作答)
解析:用1,2,3,4,5组成没有重复数字的五位数中,满足个位小于百位且百位小于万位的五位数有个,即,当时,
,
则的系数是故答案为:2022.
四、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
17.等差数列前n项和为,且,.
(1)求数列的通项公式;
(2)设数列的前n项和为,若,求n的最小值.
解:(1)设等差数列的公差为,首项为,
则,-----------------------------2分(列对一个式子得1分)
解得-----------------------------1分
所以数列的通项公式为.-----------------------------2分
(2) -----------------------------1分
----------------2分
由题得,解得-----------------------------1分
因为,所以的最小值是8.-----------------------------1分
18.下表是某高校年至年的毕业生中,从事大学生村官工作的人数:
年份
年份代码
(单位:人)
经过相关系数的计算和绘制散点图分析,我们发现与的线性相关程度很高.
(1)根据上表提供的数据,用最小二乘法求出关于的经验回归方程;
(2)根据所得的经验回归方程,预测该校年的毕业生中,去从事大学生村官工作的人数.
参考公式:
解:(1)由表格数据知-----------------------------2分
,
,-----------------------------3分
,(这里可以直接用点斜式得到下面的回归方程)
关于的经验回归方程为:.-----------------------------3分
(第一问8分)
(2)年对应的,-----------------------------1分
则,-----------------------------2分
即该校年的毕业生中,去从事大学生村官工作的人数约为人. -----------------------------1分
(如果只计算出y的值,没用文字回答扣1分)
19.某校在高一部分学生中调查男女同学对某项体育运动的喜好情况,其等高堆积条形图如图(黑色代表喜欢,白色代表不喜欢,单位:人).
(1)写出列联表;
(2)依据的独立性检验,分析喜欢这项体育运动是否与性别有关;
(3)在这次调查中,从喜欢这项体育运动的一名男生和两名女生中任选
两人进行专业培训,求恰是一男一女的概率.
附表及公式:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
,其中.
解:(1)观察题中二维条形图,可得被调查的男生总共45人,其中喜欢这项运动的有15人,不喜欢的有30人;被调查的女生总共45人,其中喜欢这项运动的有5人,不喜欢的有40人.
由此写出列联表如下:单位:人
喜欢
不喜欢
合计
男
15
30
45
女
5
40
45
合计
20
70
90
(第一问这里数据全部填对得2分,如果仅合计90填错扣1分)
(2)零假设为:喜欢这项体育运动与性别无关.--------------1分
计算可得,--------------3分
所以依据的独立性检验,没有充分证据推断不成立,因此可以认为成立,即认为喜欢这项体育运动与性别无关.--------------2分
(第二问没有零假设或假设有错扣1分,没有说明“没有充分证据推断不成立”直接说“认为成立”的扣1分,若错误回答有关的再扣1分。)我们的目的是规范答题格式。
(3)设喜欢这项体育运动的一名男生和两名女生分别为,,.任选两人的情况有,选一名男生和一名女生的情况有所以恰是一男一女的概率.
(第三问4分,可以用超几何分布来做,也可以用古典概型列举来做,大家酌情给分)
20.深圳市某高中学校组织航天科普知识竞赛,分小组进行知识问题竞答.甲乙两个小组分别从6个问题中随机抽取3个问题进行回答,答对题目多者为胜.已知这6个问题中,甲组能正确回答其中4个问题,而乙组能正确回答每个问题的概率均为.甲、乙两个小组的选题以及对每题的回答都是相互独立,互不影响的.(1)求甲小组至少答对2个问题的概率;
(2)若从甲乙两个小组中选拔一组代表学校参加全市决赛,请分析说明选择哪个小组更好?
解:(1)甲小组至少答对2道题目可分为答对2题或者答对3题;
,
所求概率-----------------------4分
(2)甲小组抽取的3题中正确回答的题数为X,则X的取值分别为1,2,3.
,-----------------------1分
结合(1)可知,-----------------------1分
.-----------------------1分
设乙小组抽取的三题中正确回答的题数为Y,则,-----------------------1分
,-----------------------1分
-----------------------1分
由,可得,甲小组参加决赛更好. -----------------------2分
(这里两个问题都不需要列出分布列表格,直接计算期望和方差。)
21.已知抛物线的焦点为F,过F的直线与抛物线C交于A,B两点,当A,B两点的纵坐标相同时,.(1)求抛物线C的方程;
(2)若P,Q为抛物线C上两个动点,,E为PQ的中点,求点E纵坐标的最小值.
解:(1)由题设,且,则,-----------------------2分
所以抛物线C的方程.-----------------------1分
(2)设直线为,
联立抛物线可得,
所以,即,
,,-----------------------2分
则,故,-----------------------1分
又,-----------------------1分
可得,-----------------------1分
所以-----------------------1分
设,
则,由对勾函数的性质:----------------------1分
当,时,在上递增,则最小;
当,时,在上递减,在上递增,则最小;
综上,时最小;时最小.-----------------------2分
(若此题彩用数形结合得出,当时,平行于x轴时中点的纵坐标最小,
此时针对这个正确的结论可以酌情给2分,当时,若证明过焦点时弦的中点纵坐标最小,若最后求出的结论正确也酌情给2分,过程如果说得严谨就酌情给过程步骤分。)
22.已知函数
(1)当时,求函数的单调区间;
(2)若,正实数满足,求证:
解:(1)由已知得,,,其中,
,-----------------------2分
令,可得,
所以,当时,,单调递增;当时,,单调递减.
综上,函数的单调递增区间为;单调递减区间为.-----------------------2分
(求导正确就酌情给1分,零点正确,再给1分。回答单调性要通过导数正负来判断推理,若没有导数正负就直接回答单调性且正确则扣1分,若最后单调性是因为定义域导致出错扣1分。
(2),
所以-----------------------1分
,整理得,,-----------------------1分
令,则可设得,,-----------------------1分
当时,,单调递减;当时,,单调递增;
所以,-----------------------2分
进而得到, -------------------1分
得到或-----------------------1分
又因为由题意得所以,不等式得证.-----------------------1分
2023-2024学年广东省深圳市盐田高级中学高二(上)期末数学试卷(B卷)(含解析): 这是一份2023-2024学年广东省深圳市盐田高级中学高二(上)期末数学试卷(B卷)(含解析),共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广东省深圳市盐田高级中学高二(上)期末数学试卷(含解析): 这是一份2023-2024学年广东省深圳市盐田高级中学高二(上)期末数学试卷(含解析),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年广东省深圳市盐田高级中学高二上学期期中考试数学试题含答案: 这是一份2023-2024学年广东省深圳市盐田高级中学高二上学期期中考试数学试题含答案,共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












