初中数学北师大版九年级下册1 二次函数课后作业题

这是一份初中数学北师大版九年级下册1 二次函数课后作业题，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
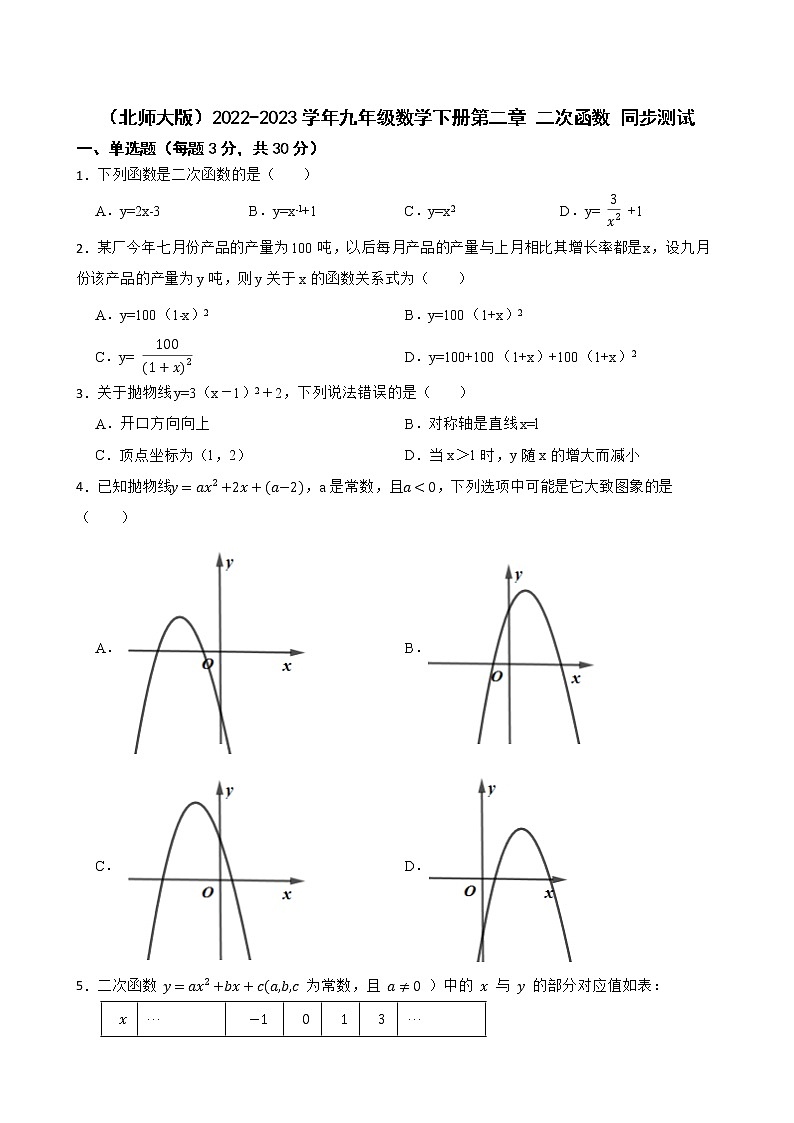
 （北师大版）2022-2023学年九年级数学下册第二章 二次函数 同步测试一、单选题（每题3分，共30分）1．下列函数是二次函数的是（　　）  A．y=2x﹣3 B．y=x﹣1+1 C．y=x2 D．y= +12．某厂今年七月份产品的产量为100吨，以后每月产品的产量与上月相比其增长率都是x，设九月份该产品的产量为y吨，则y关于x的函数关系式为（　　）  A．y=100（1﹣x）2 B．y=100（1+x）2C．y=  D．y=100+100（1+x）+100（1+x）23．关于抛物线y=3（x－1）2＋2，下列说法错误的是（　　）A．开口方向向上 B．对称轴是直线x=lC．顶点坐标为（1，2） D．当x＞1时，y随x的增大而减小4．已知抛物线，a是常数，且，下列选项中可能是它大致图象的是（　　）A． B．C． D．5．二次函数 为常数，且 ）中的 与 的部分对应值如表：  ············下列结论错误的是（　　）A．B． 是关于 的方程 的一个根；C．当 时， 的值随 值的增大而减小；D．当 时， 6．把二次函数y=﹣2x2﹣4x+3用配方法化成y=a（x﹣h）2+k的形式（　　）  A．y=﹣2（x+1）2+5 B．y=﹣2（x﹣1）2+5C．y=﹣2（x+2）2+5 D．y=2（x+1）2+57．一种包装盒的设计方法如图所示，四边形ABCD是边长为30cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四点重合于图中的点O，形成一个底面为正方形的长方体包装盒．设BE=CF=xcm，要使包装盒的侧面积最大，则x应取(　　)  A．12.5cm B．10cm C．7.5cm D．5cm8．一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内．已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（　　）  A．此抛物线的解析式是y=﹣ x2+3.5B．篮圈中心的坐标是（4，3.05）C．此抛物线的顶点坐标是（3.5，0）D．篮球出手时离地面的高度是2m9．抛物线y=2x2－2 x+1与坐标轴的交点个数是（　　）  A．0 B．1 C．2 D．310．二次函数y＝ax2+bx+c（a，b，c为常数，a≠0，c＞0）的自变量x与函数值y的部分对应值如表：  x…﹣10123…y＝ax2+bx+c…ptnt0…有下列结论：①b＞0；②关于x的方程ax2+bx+c＝0的两个根是0和3；③p+2t＜0；④m（am+b）≤﹣4a﹣c（m为任意实数）.其中正确结论的个数是（　　）A．1 B．2 C．3 D．4二、填空题（每题3分，共15分）11．如图，正方形EFGH的顶点在边长为2的正方形的边上．若设AE=x，正方形EFGH的面积为y，则y与x的函数关系为　            　．  12．平移抛物线y=2x2，使其顶点为（2，3），平移后的抛物线是　                　13．在二次函数y=-x2+bx+c中，函数y与自变量x的部分对应值如下表．x-3-2-112345y-14-7-22mn-7-14则m-n的值为　     　．14．如图，是某公园一圆形喷水池，在池中心竖直安装一根水管OA＝1.25m，A处是喷头，水流在各个方向沿形状相同的抛物线落下，水落地后形成一个圆，圆心为O，直径为线段CB．建立如图所示的平面直角坐标系，若水流路线达到最高处时，到x轴的距离为2.25m，到y轴的距离为1m，则水落地后形成的圆的直径CB＝　     　m．15．已知抛物线y= x2-2x- m-1（m为常数，nm>0）与x轴交于A、B两点（点B在点A的右侧），点P为抛物线在第四象限上的一点，抛物线的对称轴与x轴交于点H，点D在对称轴上，PD=m，取HD的中点C，连结CP、P若PR平分∠BPC；BP=2PC；则m=　     　.  三、解答题（共8题，共55分）16．关于x的函数y=（m2﹣1）x2﹣（2m+2）x+2的图象与x轴只有一个公共点，求m的值．17．已知抛物线y=ax2+bx+c如图所示，请结合图象中所给信息完成以下问题：（1）求抛物线的表达式；（2）若该抛物线经过一次平移后过原点O，请写出一种平移方法，并写出平移后得到的新抛物线的表达式．18．对于某一个函数，自变量x在规定的范围内，若任意取两个值x1和x2，它们的对应函数值分别为y1和y2．若x2＞x1时，有y2＞y1，则称该函数单调递增；若x2＞x1时，有y2＜y1，则称该函数单调递减．例如二次函数y=x2，在x≥0时，该函数单调递增；在x≤0时，该函数单调递减．（1）二次函数：y=（x+1）2+2自变量x在哪个范围内，该函数单调递减？（2）证明：函数：y=x﹣在x＞1的函数范围内，该函数单调递增．（3）若存在两个关于x的一次函数，分别记为：g=k1x+b1和h=k2x+b2，且函数g在实数范围内单调递增，函数h在实数范围内单调递减．记第三个一次函数y=g+h，则比例系数k1和k2满足何种条件时，函数y在实数范围内单调递增？19．已知二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象交于两点A（﹣2，﹣5）和B（1，4），且二次函数图象与y轴的交点在直线y=2x+3上，求这两个函数的解析式．  20．某商品每件成本40元，以单价55元试销，每天可售出100件．根据市场预测，定价每减少1元，销售量可增加10件．求每天销售该商品获利金额y（元）与定价x（元）之间的函数关系．21．如图，已知正方形OABC的边长为2，顶点A，C分别在x轴，y轴的正半轴上，E点是BC的中点，F是AB延长线上一点且FB=1．（1）求经过点O、A、E三点的抛物线解析式；（2）点P在抛物线上运动，当点P运动到什么位置时△OAP的面积为2，请求出点P的坐标；（3）在抛物线上是否存在一点Q，使△AFQ是等腰直角三角形？若存在直接写出点Q的坐标；若不存在，请说明理由．22．在平面直角坐标系xOy中，抛物线与x轴分别交于点A（2，0）、点B（点B在点A的右侧），与轴交于点C，tan∠CBA=．（1）求该抛物线的表达式；（2）设该抛物线的顶点为D，求四边形ACBD的面积；（3）设抛物线上的点E在第一象限，△BCE是以BC为一条直角边的直角三角形，请直接写出点E的坐标．23．已知：二次函数y=（n﹣1）x2+2mx+1图象的顶点在x轴上．（1）请写出m与n的关系式，并判断已知中函数图象的开口方向；（2）是否存在整数m，n的值，使函数图象的对称轴与x轴的交点横坐标为整数？若存在，请求出m，n的值；若不存在，请说明理由；（3）若y关于x的函数关系式为y=nx2﹣m2x﹣2n﹣2①当n≠0时，求该函数必过的定点坐标；②探索这个函数图象与坐标轴有两个交点时n的值．
答案解析部分1．【答案】C2．【答案】B3．【答案】D4．【答案】D5．【答案】C6．【答案】A7．【答案】C8．【答案】A9．【答案】C10．【答案】C11．【答案】y=2x2﹣4x+412．【答案】y =2（x-2）2 +313．【答案】314．【答案】515．【答案】316．【答案】解：①当m2﹣1=0，且2m+2≠0，即m=1时，该函数是一次函数，则其图象与x轴只有一个公共点； ②当m2﹣1≠0，即m≠±1时，该函数是二次函数，则△=（2m+2）2﹣8（m2﹣1）=0，解得 m=3，m=﹣1（舍去）．综上所述，m的值是1或3．17．【答案】解：（1）由题意得，解得．∴函数的解析式为：y=﹣x2﹣2x+3；（2）平移抛物线y=﹣x2﹣2x+3，使它经过原点，则平移后的抛物线解析式可为y=﹣x2﹣2x．故向下平移3个单位，即可得到过原点O的抛物线．18．【答案】解：（1）y=（x+1）2+2自变量在x≤﹣1范围内，该函数单调递减；（2）证明：任取 x2＞x1，则=（x2﹣x1）+（）=（x2﹣x1）+（）因为x2＞x1，所以y2＞y1∴y=x﹣在x＞1的函数范围内，该函数单调递增；（3）、g=k1x+b1和h=k2x+b2，且函数g在实数范围内单调递增，函数h在实数范围内单调递减，∴k1＞0，k2＜0，y=g+h即y=（k1x+b1）+（k2x+b2）=（k1+k2）x+（b1+b2）y=（k1+k2）x+（b1+b2）单调递增，∴k1+k2＞0，一次函数y=g+h，则比例系数k1和k2满足k1＞0，k2＜0，k1+k2＞0时，函数y在实数范围内单调递增．19．【答案】解：∵y=2x+3与y轴交点为（0，3），  ∴二次函数与y轴交点为（0，3），将（0，3），A（﹣2，﹣5）和B（1，4）分别代入二次函数y1=ax2+bx+c得， ，解得 ，∴二次函数的解析式为：y1=x2+2x+3；∵将A（﹣2，﹣5）和B（1，4）代入y2=mx+n得，﹣2m+n=﹣5，m+n=4，解得m=3，n=1，∴一次函数y2=mx+n的解析式为：y2=3x+120．【答案】解：由题意得，商品每件定价x元时，每件降价（55﹣x）元，销售量为[100+10（55﹣x）]件， 则y=[100+10（55﹣x）]（x﹣40）=﹣10x2+1050x﹣26000，即每天销售该商品获利金额y（元）与定价x（元）之间的函数关系式为y=﹣10x2+1050x﹣26000．21．【答案】解：（1）A的坐标是（2，0），E的坐标是（1，2）．设抛物线的解析式是y=ax2+bx+c，根据题意得：，解得：．则抛物线的解析式是y=﹣2x2+4x；（2）当△OAP的面积是2时，P的纵坐标是2或﹣2．当﹣2x2+4x=2时，解得：x=1，则P的坐标是（1，2）；当﹣2x2+4x=﹣2时，解得：x=1±，此时P的坐标是（1+，﹣2）或（1﹣，﹣2）；（3）AF=AB+BF=2+1=3．OA=2，则A是直角顶点时，Q不可能在抛物线上；当F是直角顶点时，Q不可能在抛物线上；当Q是直角顶点时，Q到AF的距离是AF=，若Q存在，则Q的坐标是（2﹣，），即（﹣，），不在抛物线上，总之Q不存在．22．【答案】解：（1）∵当x=0时，∴C（0，3），OC=3，在Rt△COB中，∵tan∠CBA=，∴=，∴OB=2OC=6，∴点B（6，0），把A（2，0）、B（6，0）分别代入y=ax2+bx+3，得：，解得：∴该抛物线表达式为y=x2﹣2x+3；（2）∵y=x2﹣2x+3=（x﹣4）2﹣1∴顶点D（4，﹣1），∴四边形ACBD的面积=△ABC的面积+△ABD的面积=×4×3+×4×1=8；（3）设点E的坐标为（x，x2﹣2x+3），分两种情况：①当∠CBE=90°时，作EM⊥x轴于M，如图所示：则∠BEM=∠CBA，∴=tan∠BEM=tan∠CBA=，∴EM=2BM，即2（x﹣6）=x2﹣2x+3，解得：x=10，或x=6（不合题意，舍去），∴点E坐标为（10，8）；②当∠BCE=90°时，作EN⊥y轴于N，如图2所示：则∠ECN=∠CBA，∴=tan∠ECN=tan∠CBA=，∴CN=2EN，即2x=x2﹣2x+3﹣3，解得：x=16，或x=0（不合题意，舍去），∴点E坐标为（16，35）；综上所述：点E坐标为（10，8）或（16，35）．23．【答案】解：（1）∵二次函数y=（n﹣1）x2+2mx+1图象的顶点在x轴上，∴4m2﹣4（n﹣1）=0，∴n﹣1=m2，∴n=m2+1，∵n﹣1≠0，且m2≥0∴n﹣1＞0，∴图象开口向上；（2）∵y=（n﹣1）x2+2mx+1，∴对称轴x=，要使为整数，∵m，n为整数，∴只要m=±1，此时n=2，∴存在m=±1，n=2，符合要求；（3）①y=nx2﹣（n﹣1）x﹣2n﹣2=n（x2﹣x﹣2）+x﹣2，令x2﹣x﹣2=0，得x=﹣1或2，所以必过的定点为（2，0），（﹣1，﹣3），②若n=0，则y=x﹣2，直线与坐标轴有两个交点，若n≠0：b2﹣4ac=（n﹣1）2+4n（2n+2）=（3n+1）2≥0，当抛物线过原点时，n=﹣1，此时图象与坐标轴有两个交点，当抛物线不过原点时，n=时，b2﹣4ac=0，图象与x轴，y轴各有1个交点，综上，当n=0或﹣1或时，函数图象与坐标轴有两个交点．