

数学4.3 中心对称课时作业
展开这是一份数学4.3 中心对称课时作业,共12页。试卷主要包含了3 中心对称,如图所示等内容,欢迎下载使用。
第4章 平行四边形
4.3 中心对称
基础过关全练
知识点1 中心对称图形与中心对称
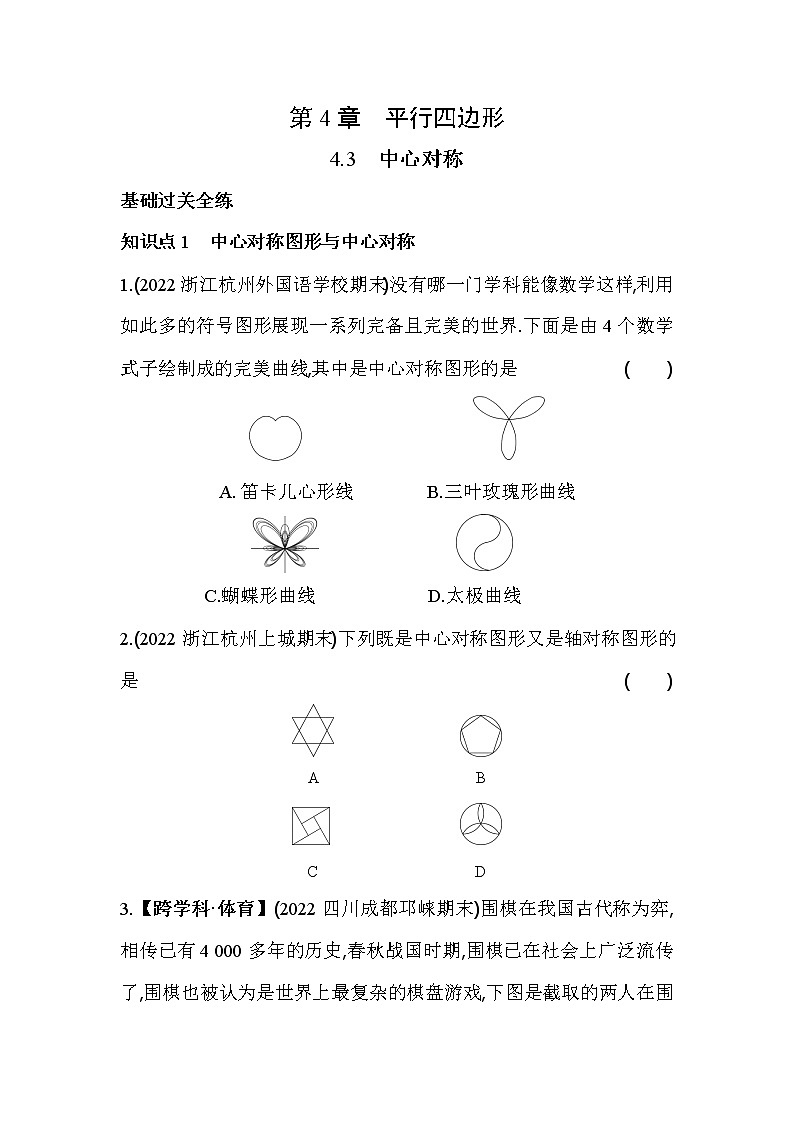
1.(2022浙江杭州外国语学校期末)没有哪一门学科能像数学这样,利用如此多的符号图形展现一系列完备且完美的世界.下面是由4个数学式子绘制成的完美曲线,其中是中心对称图形的是 ( )
- 笛卡儿心形线 B.三叶玫瑰形曲线
C.蝴蝶形曲线 D.太极曲线
2.(2022浙江杭州上城期末)下列既是中心对称图形又是轴对称图形的是 ( )
A B
C D
3.【跨学科·体育】(2022四川成都邛崃期末)围棋在我国古代称为弈,相传已有4 000多年的历史,春秋战国时期,围棋已在社会上广泛流传了,围棋也被认为是世界上最复杂的棋盘游戏,下图是截取的两人在围棋比赛中的四个部分,由黑白棋子摆成的图形是中心对称图形的是 ( )
A B
C D
4.【新独家原创】如图,图④可以通过部分图的平移、轴对称得到,则图①—图④中,忽视中心点,其中属于中心对称图形的有 个.
5.如图所示.
(1)请你画出△A'B'C',使其与△ABC关于点O成中心对称;
(2)请你在△ABC的边上找一个点M,作出△DEF,使其与△ABC关于点M成中心对称,使△DEF与△ABC合成的图形为平行四边形.
图① 图②
知识点2 中心对称图形的性质
6.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 ( )
A.点A与点A'是一对对称点
B.BO=B'O
C.∠AOB=∠A'OB'
D.∠ACB=∠C'A'B'
7.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
知识点3 作与简单图形关于已知点中心对称的图形
8.如图所示,已知线段AB和点P,求作平行四边形ABCD,使点P是它的对称中心.(不写作法,保留作图痕迹)
9.如图所示,三角形ABC和三角形A'B'C'关于某一点成中心对称,一同学不小心把墨水泼在纸上,只能看到三角形ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,并补全三角形A'B'C'.
知识点4 关于原点对称
10.在平面直角坐标系中,点A(-1,2)关于原点O对称的点A1的坐标是 ( )
A.(1,2) B.(-1,-2) C.(1,-2) D.(1,0)
11.若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
能力提升全练
12.在平面直角坐标系中,已知点A(2a-b,-8)与点B(-2,a+3b)关于原点对称,则a、b的值为 ( )
A.-2,-2 B.-2,2 C.2,-2 D.2,2
13.【新素材·益智游戏】在玩俄罗斯方块游戏时,底部已有的图形如图所示,接下去出现如下哪个形状时,通过旋转变换后能与已有图形拼成一个中心对称图形 ( )
A B
C D
14.将一张正方形纸片按如图①②所示的步骤沿虚线对折两次,然后沿图③中的虚线剪去一个角得到图④,将图④展开铺平后的图形 ( )
图① 图②
图③ 图④
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.不是轴对称图形,也不是中心对称图形
D.是中心对称图形,也是轴对称图形
15.(2022浙江湖州长兴期末,8,)如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,点A,B,C的对应点分别为A1,B1,C1,则对称中心E点的坐标是 ( )
A.(3,-1) B.(0,0) C.(2,-1) D.(-1,3)
16.如图,点O是▱ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABFE和四边形EFCD的面积分别记为S1,S2,那么S1,S2之间的关系为S1 S2.(填“>”“=”或“<”)
17.如图,直线MN过▱ABCD的对称中心O,交AD于点M,交BC于点N,已知S▱ABCD=4,则S阴影= .
18.如图,已知四边形ABCD和点P,画四边形A'B'C'D',使四边形A'B'C'D'与四边形ABCD关于点P成中心对称.
素养探究全练
19.【推理能力】数学兴趣小组活动时,提出了如下问题:如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决方法:如图①,延长AD到E,使得DE=AD,再连结BE(或将△ACD绕点D逆时针旋转180°得到△EBD).把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造关于中点中心对称的图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
迁移应用:请参考上述解题方法,回答下列问题:
如图②,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连结EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,试探索线段BE,CF,EF之间的等量关系,并加以证明.
图① 图②
答案全解全析
基础过关全练
1.D 根据中心对称图形的概念判断.选择A、B、C中的图形都不是中心对称图形,选项D中的图形是中心对称图形,故选D.
2.A
选项 | 理由 | 判断 |
A | 既是轴对称图形,又是中心对称图形 | √ |
B | 是轴对称图形,不是中心对称图形 | × |
C | 不是轴对称图形,是中心对称图形 | × |
D | 是轴对称图形,不是中心对称图形 | × |
故选A.
3.D 选项A、B、C中的图形都不能找到这样的一个点,使图形绕这一点旋转180°后与原来的图形重合,所以不是中心对称图形,选项D中的图形能找到这样的一个点,使图形绕这一点旋转180°后与原来的图形重合,所以是中心对称图形,故选D.
4.3
解析 题图①③④是中心对称图形,共3个.
5.解析 (1)如图所示,△A'B'C'即为所求.
(2)如图所示,点M,△DEF即为所求.
6.D ∵△ABC与△A'B'C'关于点O成中心对称,∴点A与点A'是一对对称点,OB=OB',∠AOB=∠A'OB',∴选项A,B,C不合题意.∵∠ACB与∠C'A'B'不是对应角,∴∠ACB=∠C'A'B'不成立,∴选项D符合题意,故选D.
7.解析 ∠B与∠F相等,理由如下:∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,∴∠B=∠DEC,∵AF∥BE,∴∠F=∠DEC,∴∠B=∠F.
8.解析 如图,平行四边形ABCD即为所求.
9.解析 如图,点O、△A'B'C'即为所求.
10.C 利用关于原点对称的点的坐标的特点进行解答即可.点A(-1,2)关于原点O对称的点A1的坐标是(1,-2),故选C.
11.A ∵点P(m,m-n)与点Q(-2,3)关于原点对称,
∴m=2,m-n=-3,解得n=5,
∴点M的坐标为(2,5),∴点M在第一象限.
故选A.
能力提升全练
12.D ∵点A(2a-b,-8)与点B(-2,a+3b)关于原点对称,
∴故选D.
13.D 如图所示,只有选项D中的图形可以与已有图形组成中心对称图形.故选D.
14.D 将题图④展开铺平后的图形大致如下:
所以题图④展开铺平后的图形是中心对称图形,也是轴对称图形.故选D.
15.A 如图,连结AA1,CC1,则交点就是对称中心E点.观察图形可知,E(3,-1).故选A.
16.=
解析 ∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠EDO=∠FBO,
∵点O是▱ABCD的对称中心,∴OB=OD,
在△DEO与△BFO中,
∴△DEO≌△BFO(ASA),∴S△DEO=S△BFO,
∵S△ABD=S△CDB,∴S1=S2.
故答案为=.
17.1
解析 ∵四边形ABCD是平行四边形,∴AM∥CN,OA=OC,∴∠MAO=∠NCO,∵∠AOM=∠CON,
∴△AOM≌△CON(ASA),∴S△AOM=S△CON,
∴S阴影=S△AOM+S△BON=S△BOC=S平行四边形ABCD=1.
18.解析 如图,四边形A'B'C'D'即为所求作的图形.
素养探究全练
19.解析 (1)证明:如图,延长FD到G,使得DG=DF,连结BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD),
易知CF=BG,DF=DG,∵DE⊥DF,∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)BE2+CF2=EF2.证明如下:
∵∠A=90°,∴∠EBC+∠FCB=90°,
易知∠FCD=∠DBG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
由(1)知BG=CF,EG=EF,∴BE2+CF2=EF2.
相关试卷
这是一份初中数学浙教版八年级下册4.3 中心对称精品课时作业,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份数学浙教版4.3 中心对称课时训练,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份初中数学浙教版八年级下册4.3 中心对称优秀同步训练题,共7页。试卷主要包含了3《中心对称》,下列图形是中心对称图形的是等内容,欢迎下载使用。













