2023年高三1月大联考（全国乙卷）理科数学试题（Word版附解析）

这是一份2023年高三1月大联考（全国乙卷）理科数学试题（Word版附解析），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
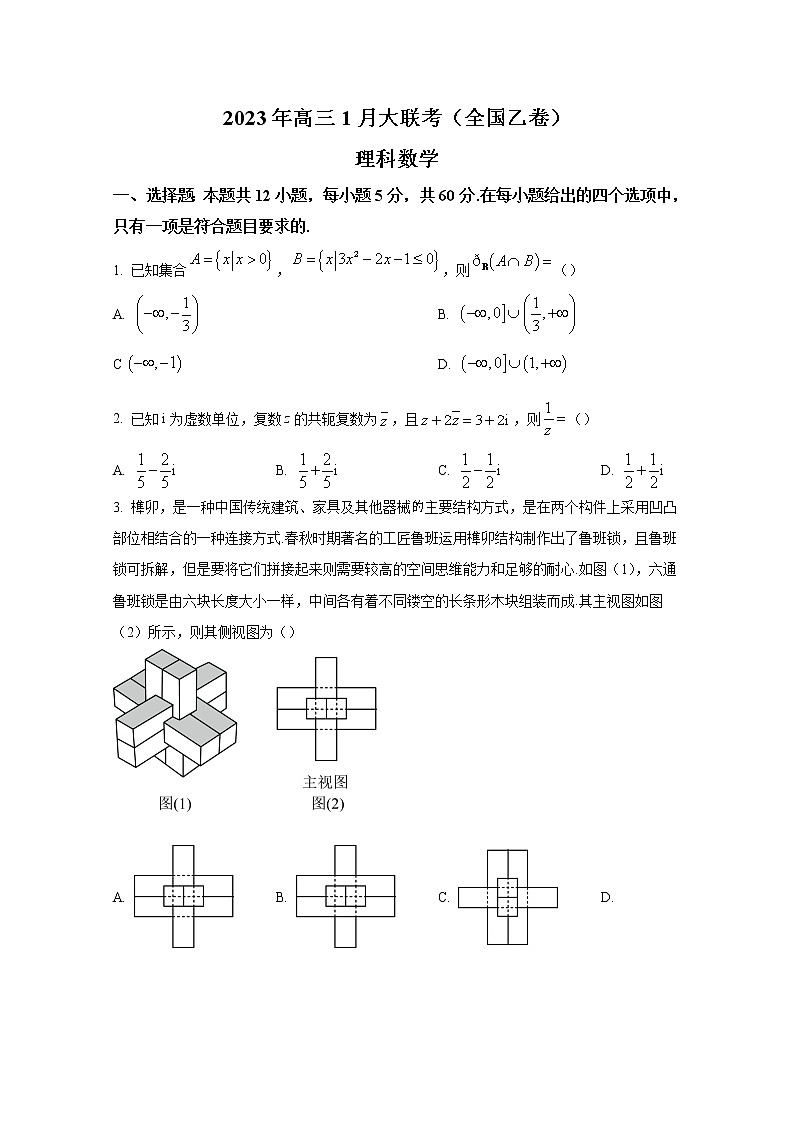
2023年高三1月大联考（全国乙卷）理科数学一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，则（）A.  B. C D. 2. 已知i为虚数单位，复数z的共轭复数为，且，则（）A.  B.  C.  D. 3. 榫卯，是一种中国传统建筑、家具及其他器械主要结构方式，是在两个构件上采用凹凸部位相结合的一种连接方式.春秋时期著名的工匠鲁班运用榫卯结构制作出了鲁班锁，且鲁班锁可拆解，但是要将它们拼接起来则需要较高的空间思维能力和足够的耐心.如图（1），六通鲁班锁是由六块长度大小一样，中间各有着不同镂空的长条形木块组装而成.其主视图如图（2）所示，则其侧视图为（） A.  B.  C.  D. 4. 已知平面向量，，且，则（）A. 1 B. 14 C.  D. 5. 已知，则（）A B.  C.  D. 6. 使得“函数在区间上单调递减”成立的一个充分不必要条件可以是（）A.  B.  C.  D. 7. 某精密仪器易因电压不稳损坏，自初装起，第一次电压不稳仪器损坏的概率为.若在第一次电压不稳仪器未损坏的条件下，第二次电压不稳仪器损坏的概率为，则连续两次电压不稳仪器未损坏的概率为（）A. 0.72 B. 0.7 C. 0.2 D. 0.188. 已知函数，将函数的图象向左平移个单位长度，再将所得函数图象上所有点的纵坐标不变，横坐标变为原来的倍得到函数的图象，若函数在上有且仅有4个零点，则实数的取值范围为（）A.  B.  C.  D. 9. 已知，，，则（）A.  B.  C.  D. 10. 已知数列满足，，设的前项和为，若，不等式恒成立，则的最小值为（）A.  B. 2 C. 5 D. 611. 已知双曲线C：的左顶点为A，右焦点为F，以线段AF为直径的圆M与双曲线的一条渐近线相交于B，D两点，且满足（O为坐标原点），若圆M的面积S满足，则双曲线C的离心率e的取值范围是（）A.  B.  C.  D. 12. 已知函数定义域为R，且满足，，，，，给出下列结论：①，；②；③当时，的解集为；④若函数的图象与直线在y轴右侧有3个交点，则实数m的取值范围是.其中正确结论的个数为（）A. 4 B. 3 C. 2 D. 1二、填空题：本题共4小题，每小题5分，共20分.13. 的展开式中含项的系数为________.14. 已知数列的前n项和为，，，且对任意，都有，则________.15. 已知抛物线，其准线为l且与x轴交于点D，其焦点为F，过焦点F的直线交抛物线于A，B两点，过点A作准线l的垂线，垂足为H.若，则线段HF的长度为________.16. 如图，已知正方体的棱长为2，E，F分别为AB，BC的中点，则下列说法正确的是________.（填写所有正确说法的序号）①平面截正方体所得截面图形的周长为；②点B到平面的距离为；③平面将正方体分割成两部分，较小一部分的体积为；④三棱锥的外接球的表面积为.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17. 记的三个内角A，B，C的对边分别为a，b，c，.（1）求A；（2）若AD是角A的平分线且，求的最小值.18. 某地区一中学为了调查教师是否经常使用多媒体教学与教师年龄的关系，规定在一个月内使用多媒体上课的次数超过本月上课总次数的一半视为经常使用，否则视为不经常使用.现对120名教师进行调查统计，汇总有效数据得到如下2×2列联表： 45岁以下45岁及以上合计经常使用402060不经常使用204060合计6060120 （1）根据表中数据，判断能否有的把握认为教师是否经常使用多媒体教学与教师年龄有关？（2）若从45岁以下的被调查教师中按是否经常使用多媒体教学采用分层抽样的方式抽取6名教师，再从这6名教师中随机选取3名教师，记其中经常使用多媒体教学的教师的人数为X，求X的分布列和数学期望.附：，.0.100.050.0250.0100.0050.00127063.8415.0246.6357.87910.828 19. 如图，已知四棱锥中，平面，四边形为等腰梯形，，且，为线段的中点.（1）求证：平面；（2）求直线与平面所成角的正弦值.20. 已知椭圆的左顶点和上顶点分别为、，直线与圆相切，切点为，且.（1）求椭圆的标准方程；（2）过圆上任意一点作圆的切线，交椭圆于、两点，试判断：是否为定值？若是，求出该值，并证明；若不是，请说明理由.21. 已知函数.（1）若当时，直线与函数的图象相切，求实数a的值；（2）设，若有两个零点，求实数a的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22. 在直角坐标系xOy中，直线l的参数方程为（t为参数，）.以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为.（1）求曲线C的直角坐标方程和当时，直线l的普通力程；（2）若直线l与曲线C交于A，B两点，且与x轴交于点F，，求直线l的倾斜角.[选修4-5，不等式选讲]23. 已知函数.（1）若，求不等式的解集；（2）若的最小值为1，求实数a的取值范围.
2023年高三1月大联考（全国乙卷）理科数学一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.【1题答案】【答案】D【2题答案】【答案】B【3题答案】【答案】C【4题答案】【答案】B【5题答案】【答案】D【6题答案】【答案】C【7题答案】【答案】A【8题答案】【答案】B【9题答案】【答案】D【10题答案】【答案】C【11题答案】【答案】B【12题答案】【答案】C二、填空题：本题共4小题，每小题5分，共20分.【13题答案】【答案】9【14题答案】【答案】4039【15题答案】【答案】【16题答案】【答案】③④三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.【17题答案】【答案】（1）（2）4【18题答案】【答案】（1）有99.9%的把握认为教师是否经常使用多媒体教学与教师年龄有关（2）分布列见解析，2【19题答案】【答案】（1）证明见解析（2）【20题答案】【答案】（1）（2）是定值，证明见解析【21题答案】【答案】（1）2（2）（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]【22题答案】【答案】（1），（2）或[选修4-5，不等式选讲]【23题答案】【答案】（1）;（2）.