2022-2023学年河北省石家庄市赵县七年级（下）月考数学试卷（3月份）(含解析 )

2022-2023学年河北省石家庄市赵县七年级（下）月考数学试卷（3月份）

一、选择题（本大题共16小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）

1.  下列命题是假命题的是(    )

A. 同旁内角互补，两直线平行
B. 如果两条直线都和第三条直线平行，那么这两条直线也互相平行
C. 同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行
D. 同位角互补，两直线平行

2.  “小小竹排江中游，巍巍青山两岸走”，所描绘的图形变换主要是(    )

A. 平移变换 B. 翻折变换 C. 旋转变换 D. 以上都不对

3.  下列四个图形中，与是对顶角的是(    )

A.  B.  C.  D.

4.  的平方根是(    )

A.  B.  C.  D.

5.  下列图形中，与是同位角的是(    )

A.  B.  C.  D.

6.  如图所示，直线与相交形成了、、和中，若要确定这四个角的度数，至少要测量其中的(    )

A. 个角 B. 个角 C. 个角 D. 个角

7.  在如下所示的条件中，可以判断两条直线互相垂直的是(    )
两直线相交所成的四个角都是直角；
两直线相交，对顶角互补；
两直线相交所成的四个角都相等．

A.  B.  C.  D.

8.  下列图形中，线段的长度表示点到直线的距离的是(    )

A.  B.
C.  D.

9.  试说明“若，，，则”是真命题以下是排乱的推理过程：
因为已知；
因为，已知；
所以，等式的性质；
所以等量代换；
所以等量代换．
正确的顺序是(    )

A.  B.
C.  D.

10.  如图，沿所在直线向右平移得到，已知，，则的长为(    )

A.  B.  C.  D.

11.  若，，则的值是(    )

A.  B.  C.  D. 或

12.  如图，，交于点，，，则的度数是(    )

A.  B.  C.  D.

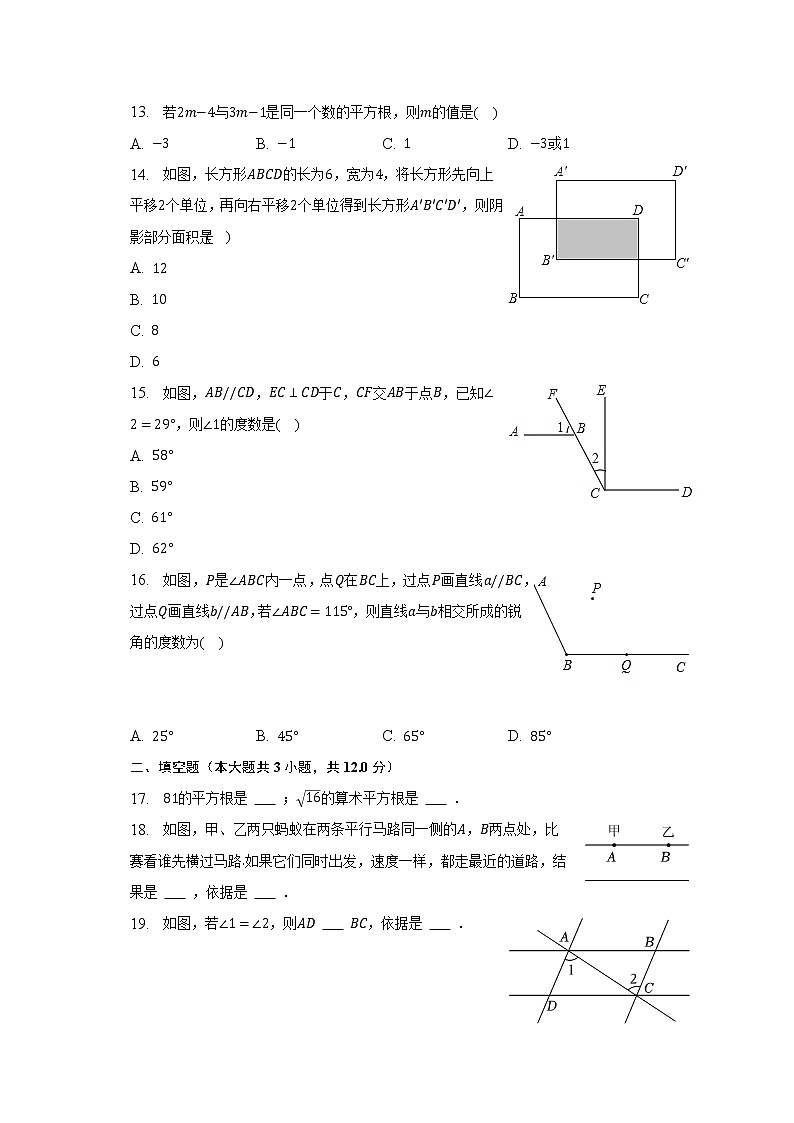
13.  若与是同一个数的平方根，则的值是(    )

A.  B.  C.  D. 或

14.  如图，长方形的长为，宽为，将长方形先向上平移个单位，再向右平移个单位得到长方形，则阴影部分面积是(    )

A.
B.
C.
D.

15.  如图，，于，交于点，已知，则的度数是(    )

A.
B.
C.
D.

16.  如图，是内一点，点在上，过点画直线，过点画直线，若，则直线与相交所成的锐角的度数为(    )

A.  B.  C.  D.

二、填空题（本大题共3小题，共12.0分）

17.  的平方根是        ；的算术平方根是        ．

18.  如图，甲、乙两只蚂蚁在两条平行马路同一侧的，两点处，比赛看谁先横过马路如果它们同时出发，速度一样，都走最近的道路，结果是        ，依据是        ．

19.  如图，若，则        ，依据是        ．

三、解答题（本大题共7小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）

20.  本小题分
求下列各数的平方根：
；
；
；
．

21.  本小题分
如图，已知：点、点及直线．
请画出从点到直线的最短路线，并写出画图的依据．
请在直线上确定一点，使点到点与点到点的距离之和最短，并写出
画图的依据．

22.  本小题分
如图，与互补，那么．
证明如下：
已知
____________
______
已知
等量代换
__________________
______

23.  本小题分
如图，直线和相交于点，平分，于点，，求的度数．

24.  本小题分
如图，、交于点，，：：，求的度数．

25.  本小题分
如图，，，平分，，，求的度数．

26.  本小题分
已知，在下列各图中，点为直线上一点，，直角三角板的直角顶点放在点处．

如图，三角板一边在射线上，另一边在直线的下方，则的度数为        ，的度数为        ；
如图，三角板一边恰好在的角平分线上，另一边在直线的下方，此时的度数为        ；
在图中，延长线段得到射线，如图，则的度数为        ；与的数量关系是        填“”、“”或“”；
如图，，在的内部，若另一边在直线的下方，则的度数为        ；的度数为       

答案和解析

1.【答案】 

【解析】解：、同旁内角互补，两直线平行，故原命题正确，是真命题，不符合题意；
B、如果两条直线都和第三条直线平行，那么这两条直线也互相平行，正确，是真命题，不符合题意；
C、同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行，正确，是真命题，不符合题意；
D、同位角相等，两直线平行，故原命题错误，是假命题，符合题意．
故选：．
利用平行线的判定方法分别判断后即可确定正确的选项．
考查了命题与定理的知识，解题的关键是了解平行线的判定方法，难度不大．
 

2.【答案】 

【解析】解：“小小竹排江中游，巍巍青山两岸走”，所描绘的图形变换主要是平移变换．
故选：．
根据平移变换，旋转变换，翻折变换的定义判断即可．
本题考查几何变换的类型，平移变换，旋转变换，翻折变换等知识，解题的关键是理解平移变换，旋转变换，翻折变换的定义，属于中考常考题型．
 

3.【答案】 

【解析】解：根据对顶角的定义可知：只有图中的是对顶角，其它都不是．
故选：．
根据对顶角的定义作出判断即可．
本题考查对顶角的定义，两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．
 

4.【答案】 

【解析】解：，
的平方根是．
故选：．
根据平方根的定义解答．
本题考查了平方根的定义，注意一个正数有两个平方根，它们互为相反数；的平方根是；负数没有平方根．
 

5.【答案】 

【解析】解：、与的对顶角是同位角，故本选项不符合题意．
B、与是同位角，故本选项符合题意．
C、与是内错角，故本选项不符合题意．
D、与是同旁内角，故本选项不符合题意．
故选：．
同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线截线的同旁，则这样一对角叫做同位角．
本题主要考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
 

6.【答案】 

【解析】

【分析】
根据对顶角的定义解答即可．
本题考查了对顶角的定义，是基础题，熟记概念并准确识图是解题的关键．
【解答】
解：根据题意可得，，
要确定这四个角的度数，至少要测量其中的个角即可．
故选：．  

7.【答案】 

【解析】解：因为两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，所以说法正确；
因为若，为两直线相交所形成的对顶角且互补，即可得得出，，则，所以两条直线垂直，故说法正确；
因为若，，，为两直线相交所形成的四个角且相得，即可得出，，则，所以所以两条直线垂直，故说法正确．
所以选项符合题意．
故选：．
根据垂线的定义进行判断即可得出答案；
根据题意可得若，，则，根据垂线的定义进行判断即可得出答案；
据题意可得若，，则，根据垂线的定义进行判断即可得出答案．
本题主要考查了垂线，余角和补角，对顶角、邻补角，熟练掌握了垂线，余角和补角，对顶角、邻补角的定义进行求解是解决本题的关键．
 

8.【答案】 

【解析】解：图、、中，线段不与直线垂直，故线段不能表示点到直线的距离；
图中，线段与直线垂直，垂足为点，故线段能表示点到直线的距离；
故选：．
根据直线外一点到这条直线的垂线段的长度，叫做点到直线的距离的概念判断．
本题考查了点到直线的距离的概念，正确理解点到直线的距离的概念是解题的关键．．
 

9.【答案】 

【解析】证明：因为，已知，
所以，等式的性质；
因为已知，
所以等量代换．
所以等量代换．
排序顺序为：．
故选：．
写出正确的推理过程，进行排序即可．
本题考查推理过程．熟练掌握推理过程，是解题的关键．
 

10.【答案】 

【解析】解：由平移的性质可知，，
，
，，
，
，
故选：．
证明即可解决问题．
本题考查平移变换，解题的关键是熟练掌握平移的性质，属于中考常考题型．
 

11.【答案】 

【解析】解：，
，，
则的值是或．
故选D．
根据平方根的定义可以求出，再利用绝对值的意义可以求出，最后即可求出的值．
本题主要考查了平方根的定义和绝对值的意义．如果，则是的平方根．若，则它有两个平方根并且互为相反数，我们把正的平方根叫的算术平方根；任何数的绝对值都是非负数，正数的绝对值是它本身，负数的绝对值是它相反数．
 

12.【答案】 

【解析】解：，
，
，
，
．
故选：．
由垂直的定义与，即可求得的度数，又由直线，根据两直线平行，内错角相等，即可求得的度数．
此题考查了平行线的性质与垂直的定义．此题比较简单，注意掌握两直线平行，内错角相等定理的应用，注意数形结合思想的应用．
 

13.【答案】 

【解析】解：当时，，
当时，．
故选：．
依据平方根的性质列方程求解即可．
本题主要考查的是平方根的性质，明确与相等或互为相反数是解题的关键．
 

14.【答案】 

【解析】解：长方形先向上平移个单位，再向右平移个单位得到长方形，
，，
，
延长交于，交于，交于，
，，
易得四边形、四边形都为矩形，
，，
阴影部分面积．
故选：．
利用平移的性质得到，，则，延长交于，交于，交于，根据平移的性质得到，，易得四边形、四边形都为矩形，然后计算出和后可得到阴影部分面积．
本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．
 

15.【答案】 

【解析】

【分析】
本题考查了平行线的性质，垂直的定义，熟练掌握平行线的性质是解题的关键．
由，得到，根据平角得到，根据平行线的性质即可得到结论．
【解答】
解：延长到，

，
，
，
，
，
．  

16.【答案】 

【解析】解：，
，
，
，
，
，
故选：．
首先根据题意画出图形，再根据两直线平行，同旁内角互补可得，再根据两直线平行，内错角相等可得的度数．
此题主要考查了平行线的性质，关键是掌握两直线平行，同旁内角互补；两直线平行，内错角相等．
 

17.【答案】   

【解析】解：的平方根是；
的算术平方根是，
故填；．
前面题目可以根据平方根的定义求出结果；
后面题目先根据算术平方根的定义化简，然后即可求出其结果的算术平方根．
此题主要考查了平方根、算术平方根的定义，要求学生理解并区分平方根、算术平方根的概念；特别注意．
 

18.【答案】同时到达  平行线间的距离处处相等 

【解析】解：点到直线之间，垂线段最短，
两只蚂蚁走的都是垂线段，
平行线间的距离处处相等，它们同时出发，速度一样，
它们同时到达；
故答案为：同时到达，平行线间的距离处处相等．
根据垂线段最短，以及平行线间的距离处处相等，进行作答即可．
本题考查平行线间的距离．熟练掌握平行线间的距离处处相等，是解题的关键．
 

19.【答案】  内错角相等，两直线平行 

【解析】解：若，，依据是内错角相等，两直线平行．
故答案为：，内错角相等，两直线平行．
根据内错角相等，两直线平行，进行作答即可．
本题考查平行线的判定．熟练掌握内错角相等，两直线平行，是解题的关键．
 

20.【答案】解：；
；
；
． 

【解析】根据平方根的定义，进行求解即可；
根据平方根的定义，进行求解即可；
根据平方根的定义，进行求解即可；
根据平方根的定义，进行求解即可．
本题考查求一个数的平方根．熟练掌握平方根的定义，是解题的关键．正数有两个不同的平方根，它们是互为相反数，的平方根是，负数没有平方根．
 

21.【答案】解：如图所示：点为所求，根据垂线段最短；

如图所示：根据两点之间线段最短． 

【解析】过作；
连接，与交点就是．
此题主要考查了垂线段的性质和线段的性质，关键是掌握垂线段最短；两点之间线段最短．
 

22.【答案】解：同旁内角互补，两直线平行
两直线平行，同位角相等
内错角相等，两直线平行
 两直线平行，同位角相等． 

【解析】证明：已知
同旁内角互补两直线平行
两直线平行同位角相等
已知
等量代换
内错角相等两直线平行
两直线平行同位角相等．
故答案为；同旁内角互补，两直线平行；两直线平行，同位角相等； ；；内错角相等，两直线平行；两直线平行，同位角相等．
利用平行线的判定和性质一一判断即可．
本题考查平行线的性质和判定，角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

23.【答案】解：，
，
，
，
平分，
，
，
． 

【解析】根据垂直，可得的度数，根据角平分线，可得的度数，于是得到结论．
本题主要考查垂线的定义、角平分线的定义、对顶角的性质、关键在于熟练运用各性质定理，推出相关角的度数．
 

24.【答案】解：平分，
，
：：，
．
，
，
解得，
． 

【解析】根据角平分线的定义得，由：：得根据平角的定义有，则，可解得出，而根据对顶角相等有，然后把、的度数代入计算即可．
本题考查了角度的计算：利用几何图形计算角的和与差．关键是根据角平分线的定义解答．
 

25.【答案】解：，，
，
，
，
，
又，
，
平分，
，
，
，
． 

【解析】推出，根据平行线性质求出，求出，根据角平分线求出，根据平行线的性质推出，代入即可．
本题考查了平行线的性质和判定，平行公理及推论，注意：平行线的性质有两直线平行，同位角相等，两直线平行，内错角相等，两直线平行，同旁内角互补．
 

26.【答案】             

【解析】解：，与互补，，
，．
故答案为：；．
三角板一边恰好在的角平分线上，，
，
又，
．
故答案为：．
对顶角，，
，
又，
．
故答案为：；．
，
与互余，
三角板里面的角，
，
，
，
，
．
故答案为：；．
利用两角互补，即可得出结论；
根据平分，可得出，由可求得的度数；
根据直角三角板各角的度数以及图中各角的关系即能得出结论；
根据直角三角板各角的度数以及图中各角的关系即能得出结论．
本题考查了角的计算，解题的关键是利用角间的各种关系，利用互余、互补即可解决问题．