2023年浙江省杭州市初中学业水平考试第一次适应性测试数学试卷（含答案）

这是一份2023年浙江省杭州市初中学业水平考试第一次适应性测试数学试卷（含答案），共12页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
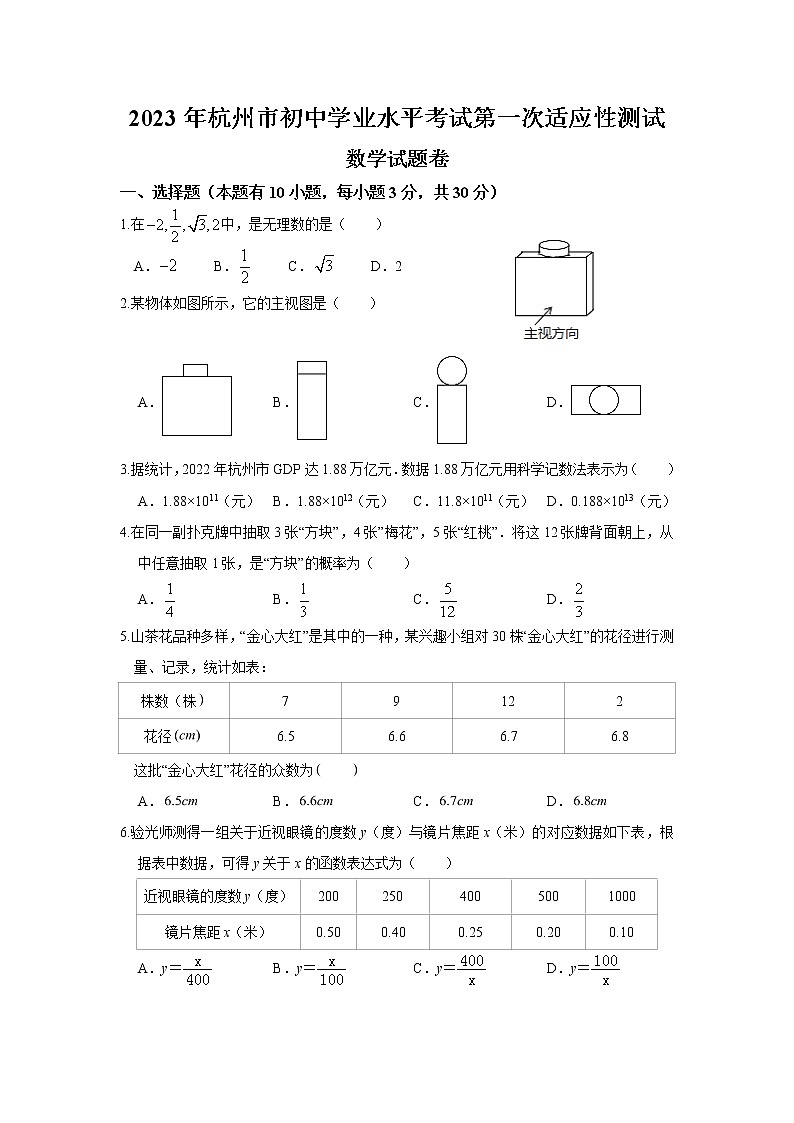
2023年杭州市初中学业水平考试第一次适应性测试数学试题卷一、选择题（本题有10小题，每小题3分，共30分）1.在中，是无理数的是（    ）A．     B．     C．     D．22.某物体如图所示，它的主视图是（    ） A． B． C． D．3.据统计，2022年杭州市GDP达1.88万亿元．数据1.88万亿元用科学记数法表示为（　　）A．1.88×1011（元） B．1.88×1012（元） C．11.8×1011（元） D．0.188×1013（元）4.在同一副扑克牌中抽取3张“方块”，4张”梅花”，5张“红桃”．将这12张牌背面朝上，从中任意抽取1张，是“方块”的概率为（　　）A． B． C． D．5.山茶花品种多样，“金心大红”是其中的一种，某兴趣小组对30株“金心大红”的花径进行测量、记录，统计如表：株数（株79122花径6.56.66.76.8这批“金心大红”花径的众数为　　A． B． C． D．6.验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表，根据表中数据，可得y关于x的函数表达式为（　　）近视眼镜的度数y（度）2002504005001000镜片焦距x（米）0.500.400.250.200.10A．y＝ B．y＝ C．y＝ D．y＝ 7.照相机成像应用了一个重要原理，用公式表示，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离．已知f，u，则u＝（    ）A．   B．   C．   D．8.如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内），已知AB＝a，AD＝b，∠BCO＝x，则点A到OC的距离等于（　　）A．asinx+bsinx      B．acosx+bcosx C．asinx+bcosx     D．acosx+bsinx     （第8题图）                       （第9题图）9.如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E,设，，则(     )A.   B. C. D. 10.在平面直角坐标系中，已知a≠b，设函数y＝（x+a）（x+b）的图象与x轴有M个交点，函数y＝（ax+1）（bx+1）的图象与x轴有N个交点，则（　　） A．M＝N﹣1或M＝N+1 B．M＝N﹣1或M＝N+2 C．M＝N或M＝N+1 D．M＝N或M＝N﹣1二、填空题（本大题有6个小题，每小题4分，共24分）11.因式分解：4﹣a2＝　   　．12.某计算机程序第一次算得m个数据的平均数为x，第二次算得另外n个数据的平均数为y，则这m+n个数据的平均数等于　   　．13.如图是一个圆锥形冰淇淋外壳（不计厚度），已知其母线长为10cm，底面圆半径为4cm，则这个冰淇淋外壳的侧面积等于　   　cm2（结果精确到个位）．                                        （第13题图）14．已知一次函数与（k是常数，）的图象的交点坐标是（2，-1），则方程组的解是_________．15.如图，⊙O分别切∠BAC的两边AB，AC于点E，F，点P在优弧（）上，若∠BAC＝66°，则∠EPF等于　   　度．（第15题图）                                   （第16题图）16.如图是一张矩形纸片，点E在AB边上，把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，连接DF若点E，F，D在同一条直线上，，则DF=______，BE=______．三．解答题(本大题有7个小题，共66分。解答应写出文字说明、证明过程或演算步骤)17．（6分）化简：﹣﹣1圆圆的解答如下：﹣﹣1＝4x﹣2（x+2）﹣（x2﹣4）＝﹣x2+2x圆圆的解答正确吗？如果不正确，写出正确的答案．

            18.（8分）某工厂生产某种产品，3月份的产量为5000件，4月份的产量为10000件．用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测，并将检测结果分别绘制成如图所示的扇形统计图和频数直方图（每组不含前一个边界值，含后一个边界值）已知检测综合得分大于70分的产品为合格产品．
（1）求4月份生产的该产品抽样检测的合格率；
（2）在3月份和4月份生产的产品中，估计哪个月的不合格件数最多？为什么？
 
    （第18题图）

  19．（8分）如图，在△ABC中，AC＜AB＜BC．（1）已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B．（2）以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ．若∠AQC＝3∠B，求∠B的度数．（第19题图）        20．（本题满分10分）设函数，函数（，，b是常数，，）．（1）若函数和函数的图象交于点，点B（3，1），①求函数，的表达式：②当时，比较与的大小（直接写出结果）．（2）若点在函数的图象上，点C先向下平移2个单位，再向左平移4个单位，得点D，点D恰好落在函数的图象上，求n的值．      21．（10分）如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．（第21题图）      22．（本题满分12分）设二次函数（b，c是常数）的图象与x轴交于A,B两点．（1）若A，B两点的坐标分别为（1，0），（2，0），求函数的表达式及其图象的对称轴．（2）若函数的表达式可以写成（h是常数）的形式，求的最小值．（3）设一次函数（m是常数）．若函数的表达式还可以写成的形式，当函数的图象经过点时，求的值．                    23．（12分）如图，已知锐角三角形ABC内接于圆O，OD⊥BC于点D，连接OA．（1）若∠BAC＝60°，①求证：OD＝OA．②当OA＝1时，求△ABC面积的最大值．（2）点E在线段OA上，OE＝OD，连接DE，设∠ABC＝m∠OED，∠ACB＝n∠OED（m，n是正数），若∠ABC＜∠ACB，求证：m﹣n+2＝0．（第23题图）                      2023年杭州市初中学业水平考试第一次适应性测试数学参考答案一．选择题：本大题有10个小题，每小题3分，共30分．题号12345678910答案CABACDBDDC二．填空题：本大题有6个小题，每小题4分，共24分．11．  12．  13．12614．  15．57°  16．2；17.解：圆圆的解答错误，正确解法：﹣﹣1＝﹣﹣＝＝＝﹣． 18.解：（1），
答：4月份生产的该产品抽样检测的合格率为98.4%；
（2）估计4月份生产的产品中，不合格的件数多，
理由：3月份生产的产品中，不合格的件数为，
4月份生产的产品中，不合格的件数为，
∵100＜160，
∴估计4月份生产的产品中，不合格的件数多．
19.解：（1）证明：∵线段AB的垂直平分线与BC边交于点P，∴PA＝PB，∴∠B＝∠BAP，∵∠APC＝∠B+∠BAP，∴∠APC＝2∠B；（2）根据题意可知BA＝BQ，∴∠BAQ＝∠BQA，∵∠AQC＝3∠B，∠AQC＝∠B+∠BAQ，∴∠BQA＝2∠B，∵∠BAQ+∠BQA+∠B＝180°，∴5∠B＝180°，∴∠B＝36°．20.解：（1）①由题意，得，所以函数．因为函数的图象过点，所以，由题意，得，解得，所以．②．（2）由题意，得点D的坐标为，所以，解得．21.解：（1）设正方形CEFG的边长为a，∵正方形ABCD的边长为1，∴DE＝1﹣a，∵S1＝S2，∴a2＝1×（1﹣a），解得，（舍去），，即线段CE的长是；（2）证明：∵点H为BC边的中点，BC＝1，∴CH＝0.5，∴DH＝＝，∵CH＝0.5，CG＝，∴HG＝，∴HD＝HG．22．（本题满分12分）解：（1）由题意，得．图象的对称轴是直线．（2）由题意，得，所以，所以当时，的最小值是．（3）由题意，得因为函数y的图象经过点，所以，所以，或．23.解：（1）①连接OB、OC，则∠BOD＝BOC＝∠BAC＝60°，∴∠OBC＝30°，∴OD＝OB＝OA；②∵BC长度为定值，∴△ABC面积的最大值，要求BC边上的高最大，当AD过点O时，AD最大，即：AD＝AO+OD＝，△ABC面积的最大值＝×BC×AD＝×2OBsin60°×＝；（2）如图2，连接OC，设：∠OED＝x，则∠ABC＝mx，∠ACB＝nx，则∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣mx﹣nx＝∠BOC＝∠DOC，∵∠AOC＝2∠ABC＝2mx，∴∠AOD＝∠COD+∠AOC＝180°﹣mx﹣nx+2mx＝180°+mx﹣nx，∵OE＝OD，∴∠AOD＝180°﹣2x，即：180°+mx﹣nx＝180°﹣2x，化简得：m﹣n+2＝0．