2023年中考数学第一轮复习：圆

这是一份2023年中考数学第一轮复习：圆，共16页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
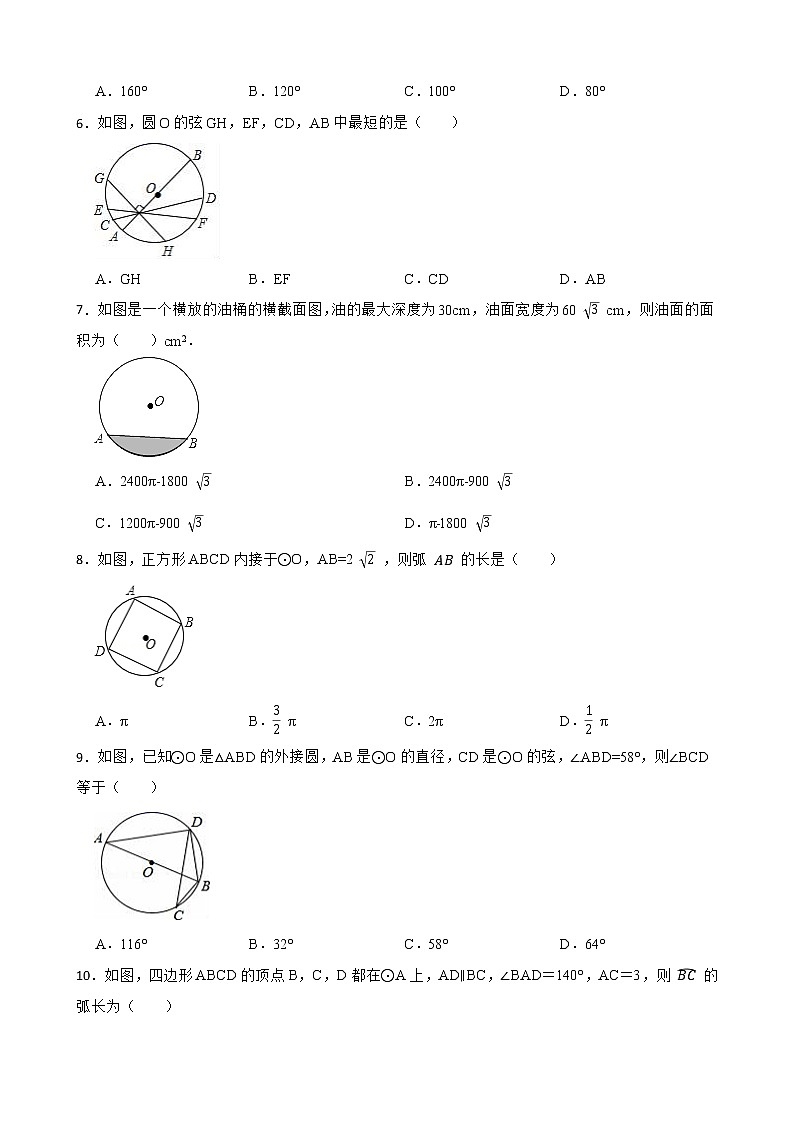
 2023年中考数学第一轮复习：圆一、单选题1．已知圆O的直径为12 ，圆心到直线 的距离为6 ，则直线 与圆O的公共点的个数为（　　）   A．2 B．1 C．0 D．不确定2．如图，AB是⊙O的直径，AB⊥CD于点E，连接CO，AD.若∠BAD＝20°，则（　　）  A．AD＝2OB B．CE＝EOC．∠OCE＝40° D．∠BOC＝2∠BAD3．在△ABC中，∠ABC=60°，∠ACB=50°，如图所示，I是△ABC的内心，延长AI交△ABC的外接圆D，则∠ICD的度数是（　　）A．50° B．55° C．60° D．65°4．如图，中，，点分别是边的中点依次以为圆心长为半径画弧得到．若在区域随机任取一点，则该点取自阴影部分的概率是（　　）A． B． C． D．5．已知圆锥的底面直径为60cm，母线长为90cm，其侧面展开图的圆心角为（　　）A．160° B．120° C．100° D．80°6．如图，圆O的弦GH，EF，CD，AB中最短的是（　　）  A．GH B．EF C．CD D．AB7．如图是一个横放的油桶的横截面图，油的最大深度为30cm，油面宽度为60 cm，则油面的面积为（　　）cm2．  A．2400π﹣1800  B．2400π﹣900 C．1200π﹣900  D．π﹣1800 8．如图，正方形ABCD内接于⊙O，AB=2 ，则弧 的长是（　　）A．π B． π C．2π D． π9．如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（　　）A．116° B．32° C．58° D．64°10．如图，四边形ABCD的顶点B，C，D都在⊙A上，AD∥BC，∠BAD＝140°，AC＝3，则 的弧长为（　　）  A． π B． π C． π D． π11．如图， 过点B、C，圆心O在等腰 的内部， ， ， .则 的半径为（　　）  A．5 B． C． D．12．如图，以AB为直径的⊙O与弦CD相交于点E，且AC=2，AE= ，CE=1．则 的长是（　　）  A． B． C． D．二、填空题13．如图，AD是⊙O的直径，于E，若DE＝3，BC＝8，则⊙O的半径为　     　.14．如图，与正五边形ABCDE的边AB、DE分别相切于点B、D，则劣弧所对的圆心角的大小为　     　度．15．如图，AB是⊙O的直径，点C是⊙O上的一点，若BC＝3，AB＝5，OD⊥BC于点D，则OD的长为　     　．16．如图， 是半圆O的直径，以O为圆心，C为半径的半圆交 于C、D两点，弦 切小半圆于点E.已知 ， ，则图中阴影部分的面积为　     　（结果保留 ）  17．如图，AB是⊙O的直径，弦CD垂直AB，已知AC=1，BC=2 ，那么sin∠ACD的值是　     　．18．半径为1的圆中最长的弦长等于​ 　     　三、综合题19．如图，点E为矩形ABCD的边BC的中点，以DE为直径的⊙O交AD于H点，过点H作HF⊥AE于点F．  （1）求证：HF是⊙O的切线；  （2）若DH=3，AF=2，求⊙O的半径．  20．如图，在圆O中，AB为直径，EF为弦，连接AF，BE交于点P，且EF2＝PF•AF.（1）求证：F为弧BE的中点；   （2）若tan∠BEF＝ ，求cos∠ABE的值.        21．已知：如图线段 ．  求作：以 为斜边的直角 ，使得一个内角等于30°．作法：①作线段 的垂直平分线交 于点 ；②以点 为圆心， 长为半径画圆；③以点 为圆心， 长为半径画弧，与 相交，记其中一个交点为 ；④分别连接 ． 就是所求作的直角三角形．（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；（2）完成下面的证明．证明：连接 ， 是 的直径，    ▲    °（    ▲    ）（填推理的依据）． 是以 为斜边的直角三角形． ， 是等边三角形． ．    ▲    °．22．如图1，AB是⊙O的直径，C，D是⊙O上的点，连接CB，CD，延长CA，BD交于点E，∠BDC=2∠ABE．（1）求证：AE=AB；（2）如图2，过点D作⊙O的切线交AE于点F，若DF=，CD=，求EF长．      23．如图，在中，，以为圆心，的长为半径的圆交边于点，点在边上且，延长交的延长线于点．（1）求证：是圆的切线；（2）已知，，求长度及阴影部分面积．  24．实践操作：如图，在 中，∠ABC=90°，利用直尺和圆规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）：（1）作∠BCA的角平分线，交AB于点O；（2）以O为圆心，OB为半径作圆．综合运用：在你所作的图中，（3）AC与⊙O的位置关系是（直接写出答案）；（4）若BC=6，AB=8，求⊙O的半径．
答案解析部分1．【答案】B2．【答案】D3．【答案】C4．【答案】A5．【答案】B6．【答案】A7．【答案】C8．【答案】A9．【答案】B10．【答案】A11．【答案】A12．【答案】B13．【答案】14．【答案】14415．【答案】216．【答案】17．【答案】18．【答案】219．【答案】（1）证明：连接OH，  ∵四边形ABCD为矩形，∴CD=BA，∠C=∠B=90°，∵E是BC的中点，∴CE=BE，∴△CDE≌△BAE（SAS），∴ED=EA，∴∠EDA=∠EAD，∵OD=OH，∴∠EDA=∠OHD，∴∠EAD=∠OHD，∴OH∥AE，∵HF⊥AE，∴HF⊥OH，∵点H为⊙O上，OH为⊙O的半径，∴HF是⊙O的切线（2）解：连接EH，  ∵DE是⊙O的直径，∴∠DHE=90°，∵∠C=∠B=90°，∴四边形HECD是矩形，∴CE=DH，同理：BE=AH，∵CE=BE，∴DH=AH=3，∵CB∥AD，∴∠BEA=∠EAD，∵∠HFA=∠B=90°，∴△FHA∽△BAE，∴ ，∴ ，∴AE= ，∴OD= DE= AE= × = ，∴⊙O的半径为 ．20．【答案】（1）证明：连接AE，  ∵EF2＝PF•AF，∴ ，∵∠AFE＝∠EFP，∴△AFE∽△EFP，∴∠EAF＝∠BEF， ∴ ，∴F为弧BE的中点；（2）解：连接BF、OF，OF交BE于点Q，  ∵AB是直径，∴∠AFB＝90°∵tan∠BEF＝ ，∴tan∠BAF＝ ，设BF＝3m，则AF＝4m，根据勾股定理AB＝5m，∴OB＝OF＝ m，∵ ，∴OF⊥BE，EQ＝BQ，EF＝BF＝3m，∵tan∠BEF＝ ，∴ ，∴∴BQ＝EQ＝   m，在Rt△BOQ中，cos∠ABE＝ 21．【答案】（1）解：如图所示： （2）解：如图，连接 ，  是 的直径， 90°（直径所对的圆周角等于90°）． 是以 为斜边的直角三角形， ， 是等边三角形． ， 30°．故答案为：90°，直径所对的圆周角等于90°，30°．22．【答案】（1）证明：根据同弧所对的圆周角相等，，由外角的性质得：，，，，为等腰三角形，；（2）解：连接，是圆的切线，，，，由三角形的外角的性质得：，，，，，，，，，，为等腰三角形，，由等腰三角形三线合一的性质得，，，，，在中，由勾股定理：，故．23．【答案】（1）证明：连接OD∵OD=OB∴∠OBD=∠ODB∵AC=CD∴∠A=∠ADC∵∠ADC=∠BDE∴∠A=∠EDB∵∠AOB=90°∴∠A+∠ABO=90°∴∠ODB+∠BDE=90°即OD⊥CE，又D在上∴是圆的切线；（2）解：由（1）可知，∠ODC=90°在Rt△OCD中，∴设OD=OB=4x，则OC=5x，∴∴AC=3x∴OA=OC+AC=8x在Rt△OAB中：即：解得，（-1舍去）∴AC=3，OC=5，OB=OD=4在在Rt△OCE中，∴设OE=4y，则CE=5y，∵解得，（舍去）∴∴阴影部分面积为．24．【答案】（1）解：如图所示：CO即为所求；（2）解：如图所示：⊙O即为所求；（3）解：相切（4）解：过点O连接AC与⊙O的切点E，∵BC=6，AB=8，∠ABC=90°，∴AC=10，∵CB是⊙O的切线，切点为B，∴CE=CB=6，又∵AC＝AE+CE，∴AE=AC－CE＝10-6=4，设BO=x，则EO=x，AO=6-x，在Rt△AOE中，AE2+EO2=AO2，即42+x2=（8-x）2，解得：x=3，∴⊙O的半径为3。