数学第二十八章 锐角三角函数28.2 解直角三角形及其应用同步达标检测题

28.2.2　应用举例(2)

知能演练提升

能力提升

1.如图,斜面AC的坡度(CD与AD的比)为1∶2,AC=3 m,坡顶有一旗杆BC,旗杆顶端点B与点A有一条彩带相连,若AB=10 m,则旗杆BC的高度为(　　)

A.5 m B.6 m

C.8 m D.(3+)m

2.如图,客轮在海上以30 km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1 h后到达C处,在C处测得A的方位角为北偏东20°,则C到A的距离是(　　)

A.15 km B.15 km

C.15()km D.5(+3)km

3.如图,一艘船向正北方向航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B处,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是　　　　　海里.(结果保留根号) 

4.如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC为74°,坝顶到坝脚的距离AB为6 m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,则AD的长为　　　　m.(精确到0.1 m) 

5.如图,某海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500 m处,当该军舰从B处向正西方向行驶至C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)

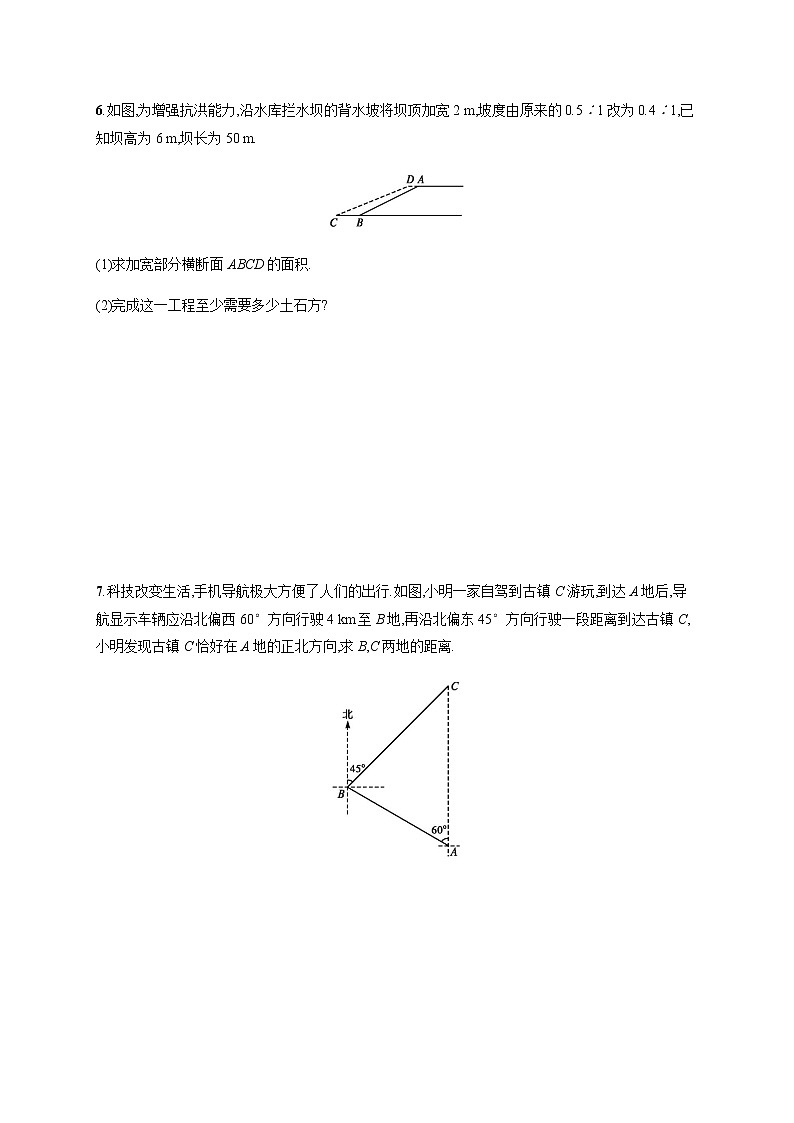
6.如图,为增强抗洪能力,沿水库拦水坝的背水坡将坝顶加宽2 m,坡度由原来的0.5∶1改为0.4∶1,已知坝高为6 m,坝长为50 m.

(1)求加宽部分横断面ABCD的面积.

(2)完成这一工程至少需要多少土石方?

7.科技改变生活,手机导航极大方便了人们的出行.如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4 km至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离.

★8.如图,某船向正东方向航行,在A处测得某岛C在北偏东60°方向,前进6海里到B,测得该岛在北偏东30°方向.已知该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁危险?请说明理由.(参考数据:≈1.732)

创新应用

★9.如图,某海关缉私艇巡逻到达A处时接到情报,在A处北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向前进,上级命令要对可疑船只进行检查,该艇立即沿北偏西45°的方向快速前进,经过1小时的航行,恰好在C处截住可疑船只,求该艇的速度.(结果保留整数,≈2.449,≈1.732,≈1.414)

能力提升

1.A

2.D　由题意得∠ACB=25°+20°=45°,∠ABC=180°-80°-25°=75°,BC=30 km.

作BD⊥AC于点D,则∠CBD=45°,

且BD=CD=15(km),

∴∠ABD=30°.

∴AD=BD·tan 30°=5(km),

∴AC=AD+CD=(5+15)km.

3.6　过点S作AB的垂线,垂足为C.

设此船继续沿正北方向航行过程中距灯塔S的最近距离SC为x海里,则=12,

解得x=6.

4.2.4　如图,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.

在Rt△ABE中,sin∠ABE=,

∴AE=ABsin∠ABE=6sin 74°≈5.77(m).cos∠ABE=,

∴BE=ABcos∠ABE=6cos 74°≈1.65(m).

∵AH∥BC,∴DF=AE≈5.77(m).

在Rt△BDF中,tan∠DBF=,

∴BF=≈4.04(m).

∴AD=EF=BF-BE≈4.04-1.65≈2.4(m).

5.解 由已知,可得∠ACB=30°.

在Rt△ABC中,∠ACB=30°,AB=500 m.

因为tan∠ACB=,

所以BC==500÷=500(m).

因此该军舰行驶的路程为500 m.

6.解 (1)分别过点A,D作AE⊥BC于点E,DF⊥BC于点F,则AE=DF=6 m.

∵AE∶BE=0.5∶1,DF∶CF=0.4∶1,

∴BE=12 m,CF=15 m.

∵EF=AD=2 m,

∴CE=CF+EF=15+2=17(m),

∴CB=CE-BE=17-12=5(m).

∴S梯形ABCD=(AD+BC)·AE=×(2+5)×6=21(m2).

(2)完成这一工程至少需要土石方21×50=1 050(m3).

7.解 如图,过点B作BH⊥AC于点H,

在Rt△ABH中,AB=4 km,∠BAH=60°,

∴sin 60°=,

∴BH=AB=×4=2(km).

在Rt△CBH中,∠CBH=45°,BH=2 km,cos 45°=,

∴BC=BH=×2=2(km).

答:B,C两地的距离为2 km.

8.解 该船继续向东航行,有触礁的危险.

过点C作CD垂直AB的延长线于点D,

因为∠CBD=60°,所以∠BCD=30°.

设CD的长为x海里,则tan∠CBD=,

所以BD=x海里.

由tan∠CAB=tan 30°=,

解得x=3.

而x≈5.2<6,所以该船继续向东航行,有触礁的危险.

创新应用

9.解 设OA的长为x海里,因为点C在点A的北偏西45°的方向上,

所以OC=OA=x海里.

根据题意,得tan 30°=,

所以,

所以x=12+12.

在Rt△OAC中,AC2=x2+x2,

所以AC=x≈46(海里).

所以该艇的速度约是46海里/时.