

人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆第2课时同步训练题
展开第2课时 圆锥的侧面积和全面积
知能演练提升
一、能力提升
1.若圆锥的轴截面为等边三角形,则称此圆锥为正圆锥,正圆锥侧面展开图的圆心角的度数为( )
A.90° B.120° C.150° D.180°
2.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),若圆锥底面圆的直径是60 cm,则这块扇形铁皮的半径是( )
A.40 cm B.50 cm C.60 cm D.80 cm
3.已知点O为一圆锥的顶点,点M为该圆锥底面上一点,点P在母线OM上,一只蚂蚁从点P出发,绕圆锥侧面爬行,回到点P时所爬过的最短路线的痕迹如图所示.若沿母线OM将圆锥侧面剪开并展开,则所得侧面展开图是( )
4.如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12 cm,OA=13 cm,则扇形AOC中的长是 cm.(计算结果保留π)
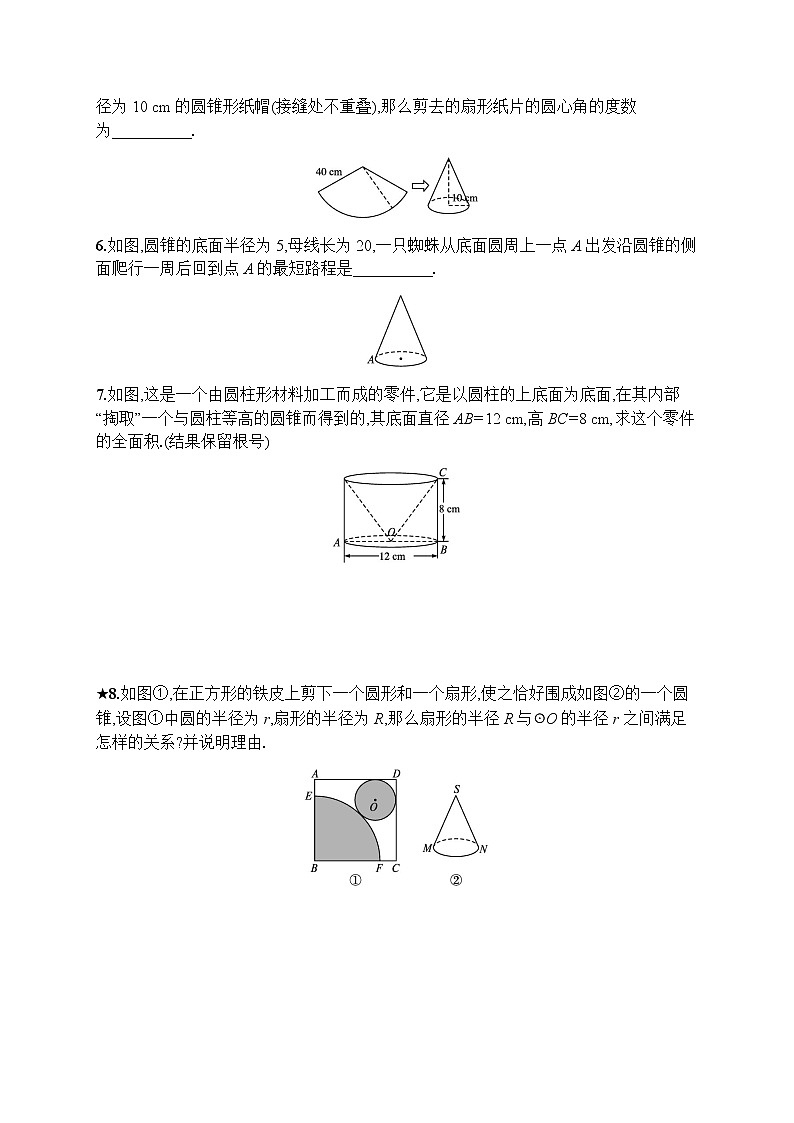
5.现有弧长为30%圆周的一个扇形彩纸片,该扇形的半径为40 cm,小红为了在六一儿童节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为10 cm的圆锥形纸帽(接缝处不重叠),那么剪去的扇形纸片的圆心角的度数为 .
6.如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是 .
7.如图,这是一个由圆柱形材料加工而成的零件,它是以圆柱的上底面为底面,在其内部“掏取”一个与圆柱等高的圆锥而得到的,其底面直径AB=12 cm,高BC=8 cm,求这个零件的全面积.(结果保留根号)
★8.如图①,在正方形的铁皮上剪下一个圆形和一个扇形,使之恰好围成如图②的一个圆锥,设图①中圆的半径为r,扇形的半径为R,那么扇形的半径R与☉O的半径r之间满足怎样的关系?并说明理由.
二、创新应用
★9.如图,一个纸杯的母线延长后相交于一点,形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯上开口圆的直径是6 cm,下底圆直径为4 cm,母线长EF=8 cm.求扇形OAB的圆心角及这个纸杯的全面积.(面积计算结果用π表示)
知能演练·提升
一、能力提升
1.D 设圆锥侧面展开图扇形的圆心角为n°,半径为r,则圆锥的底面直径也为r,根据圆锥侧面展开图扇形的弧长等于圆锥底面圆的周长,可得=πr,解得n=180.
2.A 设这块扇形铁皮的半径是r cm,根据题意,得=60π,解得r=40.
3.D
4.10π 扇形AOC中的长即为圆锥底面圆的周长.圆锥底面圆的半径为=5,则圆周长为2π×5=10π,故的长是10π cm.
5.18° 所用扇形的弧长是所围圆锥底面圆的周长,即20π cm,又扇形的半径为40 cm,可求扇形的圆心角为90°.因为扇形彩纸条的圆心角为360°×30%=108°,所以剪去扇形纸片的圆心角为18°.
6.20 将圆锥的侧面展开成扇形,连接AA',则蜘蛛爬行的最短路程就是线段AA'的长度.
由题意知,OA=OA'=20,=2π×5=10π,设∠AOA'=n°,
根据弧长公式可求
n==90.
所以在Rt△AOA'中,AA'==20.
7.解 这个零件的底面积为
π×=36π(cm2),
这个零件的外侧面积为
12π×8=96π(cm2),
圆锥母线长
OC==10(cm),
这个零件的内侧面积为
×12π×10=60π(cm2),
所以这个零件的全面积为
36π+96π+60π=192π(cm2).
8.分析 因为题图①中的圆形和扇形刚好围成题图②中的圆锥,所以题图①中的扇形的弧长等于☉O的周长.
解 扇形的半径R等于☉O的半径r的4倍.
理由如下:
因为=2πR×πR,☉O的周长为2πr,
且题图①中的扇形和☉O能围成题图②的圆锥,所以πR=2πr,
即R=4r.
二、创新应用
9.分析 展开图扇形的圆心角可利用圆锥底面周长等于展开图扇形的弧长来计算;纸杯的侧面积利用母线延长后的大圆锥的侧面积与小圆锥的侧面积的差来表示.
解 由题意,知
=6π cm,=4π cm.
设∠AOB=n°,AO=R cm,
则CO=(R-8)cm,
根据弧长公式,得=6π,=4π.
解得n=45,R=24.
所以扇形圆心角的度数为45°.
由R=24,得R-8=16.
所以S扇形OCD=×4π×16=32π(cm2),
S扇形OAB=×6π×24=72π(cm2).
所以S纸杯侧=S扇形OAB-S扇形OCD=72π-32π=40π(cm2).
又因为S纸杯底=π=4π(cm2),
所以S纸杯全=40π+4π=44π(cm2).
华师大版九年级下册27.3 圆中的计算问题课后复习题: 这是一份华师大版九年级下册27.3 圆中的计算问题课后复习题,共2页。试卷主要包含了 解, D等内容,欢迎下载使用。
人教版九年级上册24.4 弧长及扇形的面积第2课时同步训练题: 这是一份人教版九年级上册24.4 弧长及扇形的面积第2课时同步训练题,共3页。
人教版九年级上册24.1.1 圆第2课时同步训练题: 这是一份人教版九年级上册24.1.1 圆第2课时同步训练题,共7页。试卷主要包含了课前预习,课中强化,课后巩固等内容,欢迎下载使用。













