2023年江苏省苏州市立达中学中考零模数学试题（含答案）

初三数学阶段性诊断测试卷

一、选择题（每题3分，共24分）

1．2023的相反数是（    ）

A． B．  C．  D．

2．下面由北京冬奥会比赛项目图标组成的四个图形中，可看作轴对称图形的是（    ）

A．B．C．D．

3．国家中长期铁路网规划“八纵八横”之沿江高铁通道的通道，其中苏州段总投资约39000000000元，将39000000000用科学记数法表示为（    ）

A．  B．  C．  D．

4．下列运算正确的是（    ）

A．  B．  C．  D．

5．将一副三角板（厚度不计）如图摆放，使含30°角的三角板的斜边与含45°角的三角板的一条直角边平行，则的度数为（    ）

A．100°  B．105°  C．110°  D．120°

6．已知一组数据：111，113，115，115，116，这组数据的平均数和众数分别是（    ）

A．114，115  B．114，114  C．115，114  D．115，115

7．如果，那么下列不等式正确的是（    ）

A．  B．  C．  D．

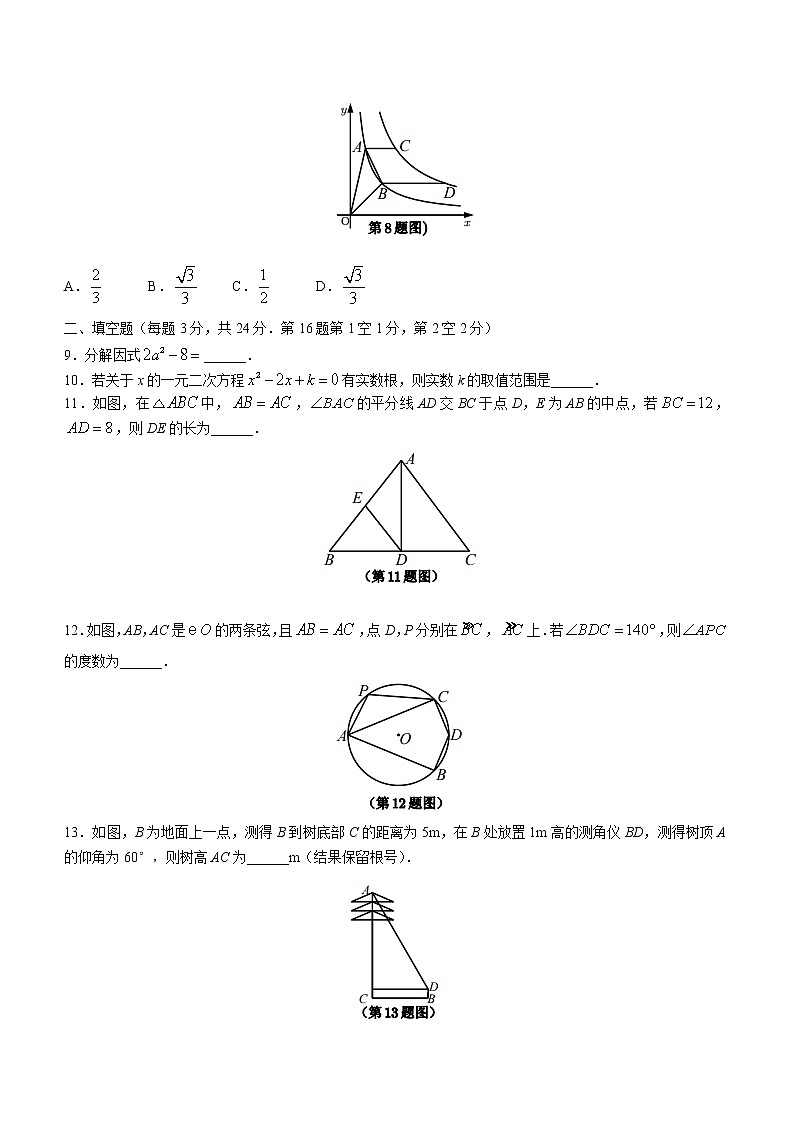
8．如图，在平面直角坐标系中，点，点在双曲线上，且，分别过点A，点B作x轴的平行线，与双曲线分别交于点C，点D．若的面积为，则的值为（    ）

A．  B．  C．  D．

二、填空题（每题3分，共24分．第16题第1空1分，第2空2分）

9．分解因式______．

10．若关于x的一元二次方程有实数根，则实数k的取值范围是______．

11．如图，在中，，的平分线AD交BC于点D，E为AB的中点，若，，则DE的长为______．

12．如图，AB，AC是的两条弦，且，点D，P分别在，上．若，则的度数为______．

13．如图，B为地面上一点，测得B到树底部C的距离为5m，在B处放置1m高的测角仪BD，测得树顶A的仰角为60°，则树高AC为______m（结果保留根号）．

14．如图，是等腰直角三角形，，，点D是斜边AB上一点，且，将绕点D逆时针旋转90°得到，交AB于点E．其中点C的运动路径为弧，则弧的长度为______．

15．如图，将沿斜边AB翻折得到，O为斜边AB的中点，连接DO并延长DO使，连接AE，已知，，则______．

16．如图，是边长为6的等边三角形，是边长为3的等边三角形，直线BD与直线AE交于点F．若点D在内，，则；现将绕点C旋转1周，在这个旋转过程中，线段AF长度的最小值是______．

三、解答题（共82分，请将答案写在答题卡上）

17．（本题共5分）计算：；

18．（本题共5分）解二元一次方程组：

19．（本题共6分）先化简再求值：，其中．

20．（本题共6分）有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2，B布袋中有三个完全相同的小球，分别标有数字1，和2．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为．

（1）用列表或画树状图的方法写出点Q的所有可能坐标；

（2）求点Q落在直线上的概率．

21．（本题共6分）在①；②；③这三个条件中任选一个合适的补充条件在下面横线上，并完成证明过程．

已知，如图，四边形ABCD是平行四边形，对角线AC，BD交于点O，点EF在AC上，______（填写序号）求证：．

22．（本题共8分）为了培养学生对航天知识的学习兴趣，某校组织全校1200名学生进行“航天知识竞赛”，从中随机抽取n名学生的竞赛成绩（满分100分，每名学生的成绩记为x分）分成四组，A组：；B组：；C组：；D组：，得到如下不完整的频数分布直方图和扇形统计图．根据图中信息，解答下列问题：

（1）n的值为______．

（2）请补全频数分布直方图，并求图中表示“C”的扇形圆心角的度数．

（3）若规定学生竞赛成绩为优秀，请估算全校竞赛成绩达到优秀的学生人数．

23．（本题共8题）第十四届国际数学教育大会（ICME—14）会徽的主题图案有着丰富的数学元素，展现了我国古代数学的文化魅力，其右下方的“卦”是用我国古代的计数符号写出的八进制数3745．八进制是以8作为进位基数的数字系统，有0~7共8个基本数字．八进制数3745换算成十进制数是，表示ICME—14的举办年份．

（1）八进制数3747换算成十进制数是______；

（2）小华设计了一个n进制数234，换算成十进制数是193，求n的值．

24．（本题共8分）如图，AB是的直径，弦CD与直径AB相交于点F，点E在外，作直线AE，且．

（1）求证：直线AE是的切线；

（2）若，，．求圆的半径r．

25．（本题共10分）在平面直角坐标系中，过一点分别作坐标轴的垂线，若两垂线与坐标轴围成矩形的周长C数值是面积S数值相等，则称这个点为“等值点”．例如：点，因为，，所以A是“等值点”．

（1）在点，，中，是“等值点”的有：______

（2）若点E为双曲线，上任意一点，将点E向右平移2个单位，再向上平移2个单位得到点F，求证：点F为“等值点”．

（3）若一次函数的图像在第一象限内有两个“等值点”，求b的取值范围．

26．（本题共10分）如图1，已知正方形ABCD中，，点P从B点出发，以的速度沿的路径匀速运动，运动到D点后立即停止运动；点Q从点C出发，以的速度沿的路径匀速运动，然后以的速度沿路径匀速运动，运动到点B后立即停止运动，若P、Q两点同时出发，设点Q的运动时间为，的面积为，y与x的函数关系如图2所示．

（1）______，______，______，______．

（2）求FG的函数表达式；

（3）时，求出以PQ为直径的圆与任一边相切时相应的x的值．

27．（本题共10分）如图（1），二次函数的图象与x轴交于A，B两点，与y轴交于C点，点B的坐标为，点C的坐标为，直线l经过B，C两点．

（1）求二次函数的表达式；

（2）点P为直线l上的一点，过点P作x轴的垂线与该二次函数的图象相交于点M，再过点M作y轴的垂线与该二次函数的图象相交于另一点N，当时，求点P的横坐标；

（3）如图（2），点C关于x轴的对称点为点D，点P为线段上BC的一个动点，连接AP；点Q为线段AP上一点，且，连接DQ，求的最小值______（直接写出答案）．

初三数学阶段性诊断测试卷（解析版）

一、选择题（每题3分，共24分）

1．B 考查知识点：相反数的概念

2．D 考查知识点：轴对称图像

3．C 考查知识点：科学计算法

4．C 考查知识点：幂的运算

5．B 考查知识点：平行线的性质，三角形内角和

6．A 考查知识点：概率统计特征值，平均数和众数的概念

7．A 考查知识点：不等式的性质

8．C 考查知识点：反比例函数

解析：设A，则  ，，，通过设点法，整体换元．

二、填空题（每题3分，共24分．第16题第1空1分，第2空2分）

9． 考查知识点：因式分解

10． 考查知识点：一元二次方程根的情况

11．5 考查知识点：等腰三角形的性质和直角三角形斜中线性质，设计到三角形中位线知识点

12．110° 考查知识点：圆的内接四边形的性质，以及圆的有关性质

13． 考查知识点：锐角三角函数的应用

14． 考查知识点：图形的旋转的性质，以及弧长公式

15． 考查知识点：图形的对称变换，轴对称的有关性质以及锐角三角函数，矩形的有关性质

解析：，在直角三角形FBC中，利用勾股定理可得，所以

16．75°，

考查知识点：图形的旋转的性质，三角形全等、隐圆问题，解三角形

解析：当AF与BF均为圆相切时，AF长度最小．  ，所以

三、解答题（共82分，请将答案写在答题卡上）

17． 3分    5分

18．  5分

19．  4分  将代入原式．  6分

20．解析：（1）图略， 2分  6种结果  ，   3分

（2）  6分

21．解析：选① ∵四边形ABCD是平行四边形 ∴，  2分

∵  ∴， ∴是平行四边形4分

∴． 6分

选② ∵四边形ABCD是平行四边形  ∴   2分

∵  ∴ ∵ ∴ 4分

∴．  6分

选③ 不得分

22．（1）60； 2分  （2）图略，144°； 6分 （3）720人 8分

23．解析：（1）2023；  3分 

（2）  5分  ，（舍负） 8分（不舍负扣1分）

24．证明：（1）∵AB是直径 ∴   2分

∵． ∴ ∴ ∴AE是的切线； 4分

（2）作于E   ∴  设， 

，，∴ ∴ 6分

∴ ∵，， 8分

25．解析：（1）D  2分

（2）点E为双曲线，上任意一点，   4分

  所以，所以点F为“等值点”．  6分

（3） ，，，∴ 8分

，，所以  10分

方法二：， ，所以：  8分

由平移与有一个公共点时，即，，，有两个公共点时，  10分

26．解析：（1），2，4，5  4分

（2）  6分

（3）与AB相切时，    

所以：      10分（每个答案1分）

27．解析：（1）  3分

（2）设，，    5分

   或 或，  8分

（3）  10分