2023年山东省济南市中考数学模拟试题（含答案）（含答案）

2023山东省 济南市 中考数学 模拟试题 （大通关）

选择题部分  共48分

一、选择题（本大题共12个小题，每小题4分，共48分．）

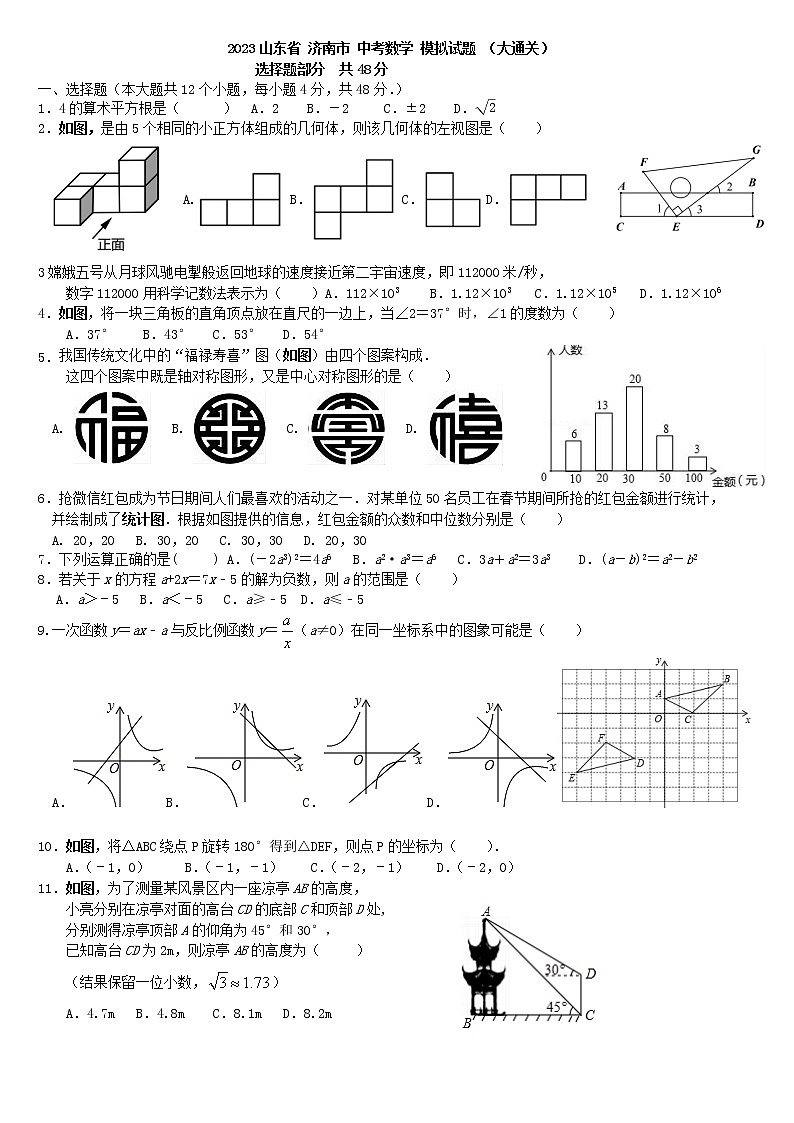
1．4的算术平方根是（      ）  A．2    B．－2     C．±2    D．

2．如图，是由5个相同的小正方体组成的几何体，则该几何体的左视图是（    ）

   A. B． C． D．            

3嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度，即112000米/秒，

数字112000用科学记数法表示为（　　）A．112×103    B．1.12×103    C．1.12×105   D．1.12×106

4．如图，将一块三角板的直角顶点放在直尺的一边上，当∠2＝37°时，∠1的度数为（    ）

A．37°    B．43°   C．53°   D．54°  

5．我国传统文化中的“福禄寿喜”图（如图）由四个图案构成．

这四个图案中既是轴对称图形，又是中心对称图形的是（　　）

A.    B.    C.    D.

6．抢微信红包成为节日期间人们最喜欢的活动之一．对某单位50名员工在春节期间所抢的红包金额进行统计，

并绘制成了统计图．根据如图提供的信息，红包金额的众数和中位数分别是（　　）

A. 20，20   B. 30，20   C. 30，30   D. 20，30

7．下列运算正确的是(     ) A．(－2a3)2＝4a6   B．a2·a3＝a6   C．3a＋a2＝3a3    D．(a－b)2＝a2－b2

8．若关于x的方程a+2x＝7x﹣5的解为负数，则a的范围是（　　）

A．a＞﹣5   B．a＜﹣5   C．a≥﹣5  D．a≤﹣5

9.一次函数y＝ax﹣a与反比例函数y＝（a≠0）在同一坐标系中的图象可能是（　　）

A．B．C．D．

10．如图，将△ABC绕点P旋转180°得到△DEF，则点P的坐标为（    ）．

A．（﹣1，0）     B．（﹣1，﹣1）    C．（﹣2，﹣1）    D．（﹣2，0）

11．如图，为了测量某风景区内一座凉亭AB的高度，

小亮分别在凉亭对面的高台CD的底部C和顶部D处,

分别测得凉亭顶部A的仰角为45°和30°，

已知高台CD为2m，则凉亭AB的高度为（     ）

（结果保留一位小数，）

A．4.7m   B．4.8m    C．8.1m   D．8.2m

12．如图1，抛物线y＝ax2＋bx＋c（a≠0）与x轴交于A（－1，0），

与y轴的交点B在（0，－2）和（0，－1）之间（不包括这两点），对称轴：x＝1,

(1)abc＞0；（2）4a＋2b＋c＞0；（3）4ac－b2＜16a；（4）＜a＜；（5）b＜c，

其中正确的结论有（     ）A.(2)(3)(4)(5)     B.(1)(3)(4)(5)    C.(1)(3)(4)    D.(1)(2)(5)

非选择题部分  共102分

二、填空题(本大题共6个小题．每小题4分，共24分．把答案填在答题卡的横线上．)

13．分解因式：2a2－2＝　      　．

14．在不透明的盒子中装有5个黑色棋子和若干个白色做子，每个棋子除颜色外都相同，

任意摸出一个棋子，摸到黑色棋子的概率是，则白色棋子的个数是　    　．

15．代数式与代数式的值相等，则x＝　      　．

16如图2，Rt△ABC中，∠ACB＝90°，分别以AC、BC、AB为直径作半圆，

三个半圆形成的两个月牙形（图中阴影部分）称为“希波克拉底月形”（希波克拉底是古希腊数学家），

若AC＝3，BC＝4，则希波克拉底月形（阴影部分）的面积等于_____．

17.如图3，将周长为6的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为______

18.如图4，在矩形ABCD中，AB＝9，E，F分别在BC，CD上，将△ABE沿AE折叠，使B落在AC上的B′处，

又将△CEF沿EF折叠，使点C落在直线EB′与AD的交点C′处，DF＝_____．

三、解答题（本大题共9个小题，共78分．解答应写出文字说明，证明过程或演算步骤．）

19.(6分) 计算：）0－2sin30°＋＋（）－1         20.（6分）解不等式组，并求其整数解

21．(6分)如图，在矩形ABCD，AD=AE，DF⊥AE于点F．求证：AB=DF．

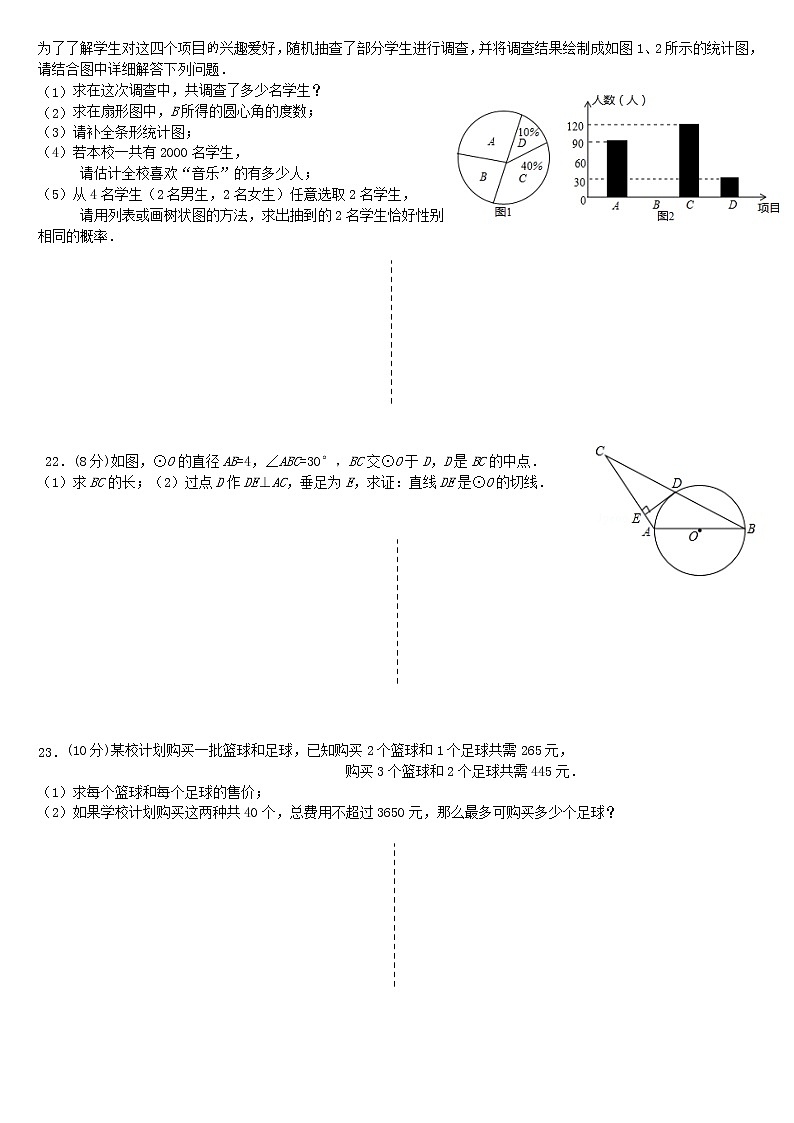
22．(8分)某小学决定开设A舞蹈、B音乐、C绘画、D书法四个兴趣班，

为了了解学生对这四个项目兴趣爱好，随机抽查了部分学生进行调查，并将调查结果绘制成如图1、2所示的统计图，

请结合图中详细解答下列问题．

（1）求在这次调查中，共调查了多少名学生？

（2）求在扇形图中，B所得的圆心角的度数；

（3）请补全条形统计图；

（4）若本校一共有2000名学生，

请估计全校喜欢“音乐”的有多少人；

（5）从4名学生（2名男生，2名女生）任意选取2名学生，

请用列表或画树状图的方法，求出抽到的2名学生恰好性别相同的概率．

 22．(8分)如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．

（1）求BC的长；（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．

23．(10分)某校计划购买一批篮球和足球，已知购买2个篮球和1个足球共需265元，

购买3个篮球和2个足球共需445元．

（1）求每个篮球和每个足球的售价；

（2）如果学校计划购买这两种共40个，总费用不超过3650元，那么最多可购买多少个足球？

25．(10分)如图1，A（0，8）、B（2，a）在直线y＝﹣2x+b上，反比例函数y＝（x＞0）的图象经过B．

（1）求a和k的值；

（2）将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，连接AC、BD．

①如图2，当m＝3时，过D作DF⊥x轴于点F，交反比例函数图象于点E，求的值；

②在线段AB运动过程中，连接BC，若△BCD是以BC为腰的等腰三形，求所有满足条件的m的值．

26．(12分)已知：正方形ABCD，等腰直角三角板的直角顶点落在正方形的顶点D处，使三角板绕点D旋转．

（1）当三角板旋转到图1的位置时，猜想CE与AF的数量关系，并加以证明；

（2）在（1）的条件下，若DE=1，AE=，CE=3，求∠AED的度数；

（3）若BC=4，点M是边AB的中点，连结DM，DM与AC交于点O，当三角板的一边DF与边DM重合时

（如图2），若OF=，求CN的长．

27．(12分)如图1，抛物线y＝－x2＋bx＋c过点A(－1，0)，点B(3，0)与y轴交于点C．

在x轴上有一动点E(m，0)(0＜m＜3)，过点E作直线l⊥x轴，交抛物线于点M．

（1）求抛物线的解析式及C点坐标；

（2）当m＝1时，D是直线l上的点且在第一象限内，若△ACD是以∠DCA为底角的等腰三角形，求点D的坐标；

（3）如图2，连接BM并延长交y轴于点N，连接AM，OM，设△AEM的面积为S1，△MON的面积为S2，

若S1＝2S2，求m的值．

2023山东省 济南市 中考数学 模拟试题（大通关）参考答案

一、选择题（本大题共12小题，每小题4分，共48分）

二、填空题13．2(a +1)(a－1)   14．15  15．7   16．6  17．8 

18．【答案】3.解：连接CC′，∵将△ABE沿AE折叠，使点B落在AC上的点B′处，

又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．∴EC＝EC′，∴∠1＝∠2，

∵∠3＝∠2，∴∠1＝∠3，在△CC′B′与△CC′D中， ，

∴△CC′B′≌△CC′D（AAS），∴CB′＝CD，

又∵AB′＝AB，∴AB′＝CB′，所以B′是对角线AC中点，即AC＝2AB＝18，

所以∠ACB＝30°，∴∠BAC＝60°，∠ACC′＝∠DCC′＝30°，

∴∠DC′C＝∠1＝60°，∴∠DC′F＝∠FC′C＝30°，∴C′F＝CF＝2DF，

∵DF+CF＝CD＝AB＝9，∴DF＝3．故答案为3．

三、19．解：原式＝1－1＋2＋2＝4．

20．不等式组的解集是-2＜x＜1，它的整数解是：-1 , 0,

21．证明：∵四边形ABCD是矩形，∴AD∥BC，∠B=90°，∴∠AEB=∠DAE，

∵DF⊥AE，∴∠AFD=∠B=90°，在△ABE和△DFA中∵  ∴△ABE≌△DFA，∴AB=DF．

22．解：（1）120÷40%＝300（名），所以在这次调查中，共调查了300名学生；

（2）B类学生人数＝300﹣90﹣120﹣30＝60（名），则B对应的圆心角度数为360°×＝72°；

（3）补全条形图如下：

（4）2000×＝400（人），所以估计喜欢“音乐”的人数约为400人；

（5）画树状图为：

共有12种等可能的结果数，其中相同性别的学生的结果数为4，所以相同性别的学生的概率＝

23．解：（2．证明：（1）解：连接AD，∵AB是⊙O的直径，∴∠ADB=90°，

又∵∠ABC=30°，AB=4，∴BD=2，∵D是BC的中点，∴BC=2BD=4；

（2）证明：连接OD．

∵D是BC的中点，O是AB的中点，∴DO是△ABC的中位线，∴OD∥AC，则∠EDO=∠CED

又∵DE⊥AC，∴∠CED=90°，∠EDO=∠CED=90°∴DE是⊙O的切线．

24．解：（1）设每个篮球和每个足球的售价分别为元，元，

根据题意得， 解得，则每个篮球和每个足球的售价分别为85元，95元；

（2）设足球购买个，则篮球购买个，根据题意得：，

整理得：，解得：a ≤ 25     则最多可购买25个足球．

25．解：（1）∵点A（0，8）在直线y＝﹣2x+b上，∴﹣2×0+b＝8，∴b＝8，∴直线AB的解析式为y＝﹣2x+8，

将点B（2，a）代入直线AB的解析式y＝﹣2x+8中，得﹣2×2+8＝a，∴a＝4，∴B（2，4），

将B（2，4）在反比例函数解析式y＝（x＞0）中，得k＝xy＝2×4＝8；

（2）①由（1）知，B（2，4），k＝8，∴反比例函数解析式为y＝，

当m＝3时，∴将线段AB向右平移3个单位长度，得到对应线段CD，∴D（2+3，4），即：D（5，4），

∵DF⊥x轴于点F，交反比例函数y＝的图象于点E，∴E（5，），

∴DE＝4﹣＝，EF＝，∴＝＝；

②如图，∵将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，∴CD＝AB，AC＝BD＝m，

∵A（0，8），B（2，4），∴C（m，8），D（（m+2，4），

∵△BCD是以BC为腰的等腰三形，∴Ⅰ、当BC＝CD时，∴BC＝AB，

∴点B在线段AC的垂直平分线上，∴m＝2×2＝4，

Ⅱ、当BC＝BD时，∵B（2，4），C（m，8），

∴BC＝，∴＝m，∴m＝5，

即：△BCD是以BC为腰的等腰三形，满足条件的m的值为4或5．

26．解：（1）CE=AF证明：∵ABCD是正方形   ∴AD=CD，∠ADC=900

∵△DEF是等腰直角三角形   ∴DE=DF，∠FDE=900

∴∠ADF+∠ADE=∠CDE+∠ADE   ∴∠ADF=∠CDE  ∴△ADF≌△CDE， ∴CE=AF

（2）设DE=   ∵ DE：AE：CE=1：：3 ∴ AE=，CE=AF=3，

∵△DEF为等腰直角三角形  ∴ EF=，∠DEF=450

∴AE2+EF2=7k2+2k2=9k2，AF2=9k2   ∴AE2+EF2=AF2      ∴△AEF为直角三角形  ∴∠AEF=90° 

∴∠AED=∠AEF+∠DEF=90°+45°=135°

（3）∵M是AB中点，  ∴MA=AB=AD，   ∵AB∥CD，  ∴，

在Rt△DAM中，DM=，∴DO=，   ∵OF=，∴DF=， 

∵∠DFN=∠DCO=45°，∠FDN=∠CDO，∴△DFN∽△DCO  

∴，∴，∴DN=   ∴CN=CD﹣DN=4﹣=

27．解：（1）由题意得 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．2分

解得

∴抛物线的解析式为y＝－x2＋2x＋3．．．．．．．．．．．．．．．．．．．．．．．．．．3分

∴点C(0，3)．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分

(2) 分两种情况讨论：

①如答案图1，当DA＝DC时，设D(1，t)，则

4＋t2＝1＋(t－3)2．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分

解得t＝1．

∴D(1， 1 )．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分

②如答案图2，当MC＝AD时，由题意得，

12＋32＝22＋t2． ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．7分

解得t＝±．

又点D在第一象限，

∴D(1，)．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分

综上： D(1，)，(1，1)．

(3)设M(m，－m2＋2m＋3)，由题意得，△BON∽△BEM．

∴＝．

∴＝．

∴ON＝3(m＋1) ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．9分

∵AE＝m＋1，

∴ON＝3AE．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．10分

∵S1＝2S2，

∴AE·EM＝2×ON·OE．

即－m2 ＋2m＋3＝6m．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．11分

∴m＝－2±．

又∵点D在第一象限，

∴m＝－2＋．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分