

中职数学高教版(中职)基础模块上册复习题2优秀单元测试当堂达标检测题
展开方程与不等式训练题B卷
一、选择题
1.不等式的解集是
A. B.
C. D.
2.集合,,则
A. B.
C. D.
3.不等式组的解集在数轴上可以表示为( )
A. B. C. D.
4若不等式|ax+2|<6的解集为(﹣1,2),则实数a等于( )
A.8 B.2 C.﹣4 D.﹣8
5.下列关于一元二次方程的说法正确的是( )
A.该方程只有一个实数根
B.该方程只有一个实数根
C.该方程的实数根为,
D.该方程的实数根为,
6.已知方程的两个根是、,那么这两个根与方程中系数的关系是( )
A. B. C. D.
7.不等式的解集为
A. B.
C. D.
8.方程的根是( )
A. B. C. D.
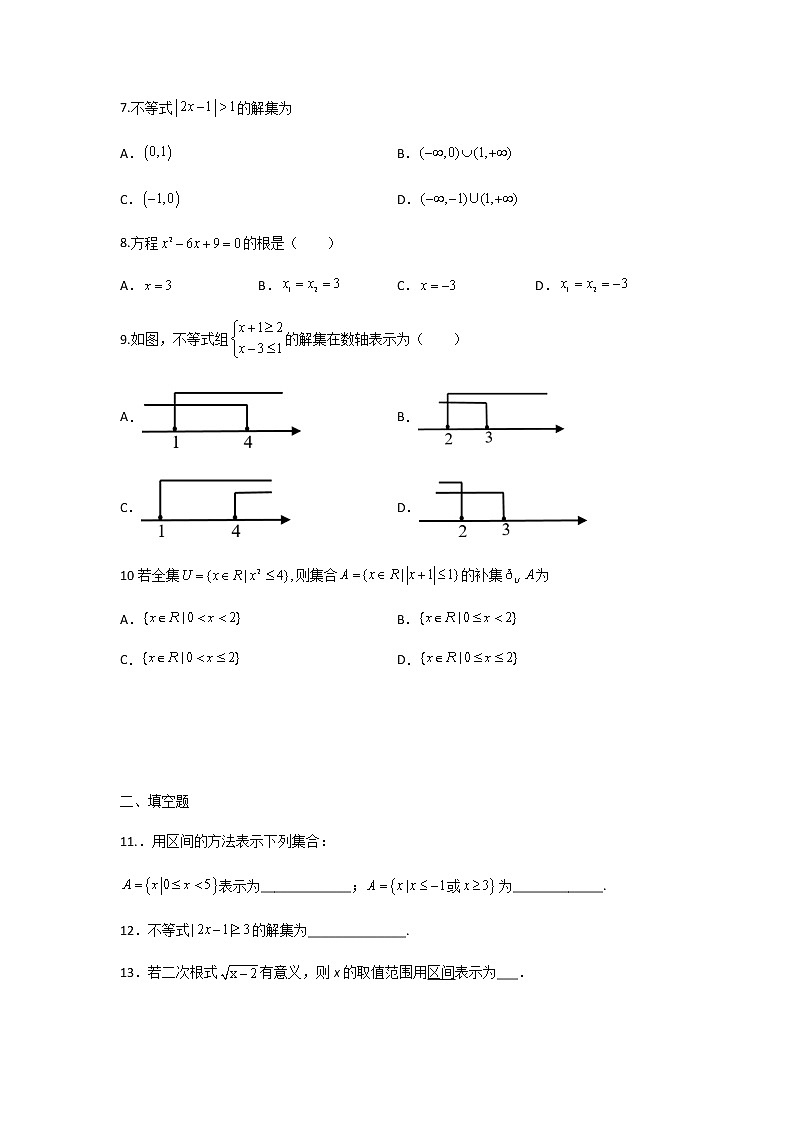
9.如图,不等式组的解集在数轴表示为( )
A. B.
C. D.
10若全集则集合的补集为
A. B.
C. D.
二、填空题
11..用区间的方法表示下列集合:
表示为_____________;或为_____________.
12.不等式的解集为______________.
13.若二次根式有意义,则x的取值范围用区间表示为___.
14.关于x的不等式|mx-2|<3的解集为,则m=________.
三、解答题
15若直角三角形的两直角边长分别是方程x2﹣14x+48=0的两根,求该直角三角形的面积?
16若,求的值?
17用区间表示不等式的解集.
18比较2x2+5x+3与x2+4x+2的大小.
19.求下列绝对值不等式的解集:
(1)
(2).
- 关于x的一元二次方程,其根的判别式的值为1,求该方程的根?
方程与不等式训练题B
一、选择题
1.不等式的解集是
A. B.
C. D.
【答案】A
【解析】因为,所以,因此,
解得.故选A
2.集合,,则
A. B.
C. D.
【答案】D
【解析】由题得N={x|-1≤x≤3,={-1,0,1,2,3},
所以.故选D
3.不等式组的解集在数轴上可以表示为( )
A. B. C. D.
【答案】D
【解析】:不等式组的解集是,
在数轴上表示为:,故选:D.
4若不等式|ax+2|<6的解集为(﹣1,2),则实数a等于( )
A.8 B.2 C.﹣4 D.﹣8
【答案】C
【解析】因为的解集为,所以和是方程的根,
所以解得.故选:C.
5.下列关于一元二次方程的说法正确的是( )
A.该方程只有一个实数根
B.该方程只有一个实数根
C.该方程的实数根为,
D.该方程的实数根为,
【答案】D
【解析】:,,
故原方程有两个不相等的实数根,解得,.故选:D.
6.已知方程的两个根是、,那么这两个根与方程中系数的关系是( )
A. B. C. D.
【答案】D
【解析】:∵方程的两个根是、,
则,
∴,,故选:D.
7.不等式的解集为
A. B.
C. D.
【答案】B
【解析】由|2x﹣1|>1得2x﹣1>1,或2x﹣1<-1
解得x>1或x<0.故选B.
8.方程的根是( )
A. B. C. D.
【答案】B
【解析】:利用完全平方公式变形后得,
即,故选:B.
9.如图,不等式组的解集在数轴表示为( )
A. B.
C. D.
【答案】A
【解析】:
解不等式组得:,
在数轴上表示为:
故选:A.
10若全集则集合的补集为
A. B.
C. D.
【答案】C
【解析】: ,补集
二填空题
11.用区间的方法表示下列集合:
表示为_____________;或为_____________.
【答案】
【解析】
表示为区间:
或表示为区间:
故答案为:
12.不等式的解集为______________.
【答案】或
【解析】由,得或,
解得或,
所以原不等式的解集为或,
故答案为:或,
13.若二次根式有意义,则x的取值范围用区间表示为___.
【答案】
【解析】由题意知,要使有意义,
则,得.
所以x的取值范围为:.
故答案为:
14.关于x的不等式|mx-2|<3的解集为,则m=________.
【答案】-6
【解析】
|mx-2|<3⇔-3<mx-2<3⇔-1<mx<5,
①若m>0,则,
由题意得且,无解.
②若m<0,则,
由题意得且,
所以m=-6,
综上可得m=-6.
故答案为:.
三解答题
15若直角三角形的两直角边长分别是方程x2﹣14x+48=0的两根,求该直角三角形的面积?
【解析】:设x1、x2是方程x2﹣14x+48=0的两根,
∴x1x2=48,
∵直角三角形的两直角边长分别是方程x2﹣14x+48=0的两根,
∴直角三角形的面积为: = =24,
故答案为:24.
16若,求的值?
【解析】:令,
原方程变形得:,
因式分解为:,
可得或,
解得:或,
∵,
∴
即:的值是4,
故答案为:4.
17用区间表示不等式的解集.
【答案】
【解析】
,即,写成区间为,
故不等式的解集为.
18.比较2x2+5x+3与x2+4x+2的大小.
【答案】2x2+5x+3>x2+4x+2.
【解析】
(2x2+5x+3)-(x2+4x+2)=x2+x+1=(x+)2+.
因为(x+)2≥0,所以(x+)2+≥>0,所以(2x2+5x+3)-(x2+4x+2)>0,
所以2x2+5x+3>x2+4x+2.
19.求下列绝对值不等式的解集:
(1)
(2).
【答案】(1);(2)
【解析】:(1)原不等式等价于,即或,解得或,所以不等式的解集为.
(2)原不等式等价于,即或,解得或.
综上,所求不等式的解集为.
20关于x的一元二次方程,其根的判别式的值为1,求该方程的根?
【解析】根据题意得:
整理得,
解得
又
原方程化为:
根据公式解得:
故答案为:
高教版(中职)基础模块上册复习题2优秀单元测试练习: 这是一份高教版(中职)基础模块上册复习题2优秀单元测试练习,共8页。试卷主要包含了选择题等内容,欢迎下载使用。
中职数学复习题1优秀单元测试巩固练习: 这是一份中职数学复习题1优秀单元测试巩固练习,共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
中职数学高教版(中职)基础模块上册复习题1优秀单元测试课后练习题: 这是一份中职数学高教版(中职)基础模块上册复习题1优秀单元测试课后练习题,共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












