






还剩22页未读,
继续阅读
所属成套资源:高中数学新教材必修第二册同步课件PPT
成套系列资料,整套一键下载
高中数学新教材必修第二册课件PPT 第7章 章末复习课
展开
这是一份高中数学新教材必修第二册课件PPT 第7章 章末复习课,共30页。
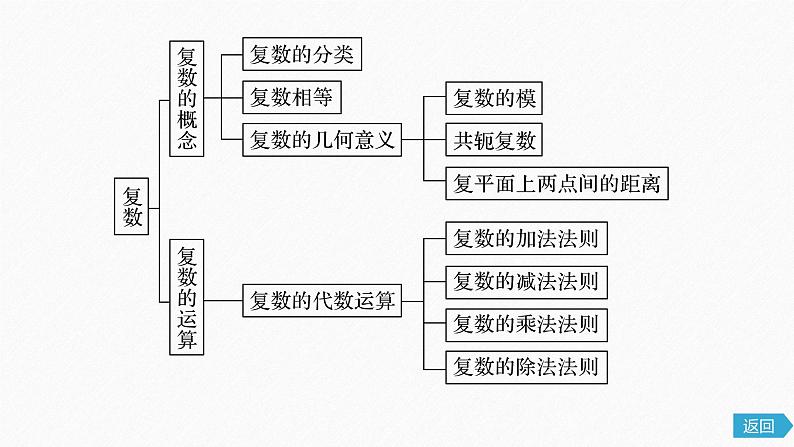
高中数学新教材同步课件必修第二册 高考政策|高中“新”课程,新在哪里?1、科目变化:外语语种增加,体育与健康必修。第一,必修课程,由国家根据学生全面发展需要设置,所有学生必须全部修习、全部考试。第二,选择性必修课程,由国家根据学生个性发展和升学考试需要设置。第三,选修课程,由学校根据实际情况统筹规划开设,学生自主选择修习。2、课程类别变化,必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下,对原必修课程学分进行重构,由必修课程学分、选择性必修课程学分组成,适当增加选修课程学分。3、学时和学分变化,高中生全年假期缩减到11周。4、授课方式变化,选课制度将全面推开。5、考试方式变化,高考统考科目由教育部命题,学业水平合格性、等级性考试由各省命题。章末复习课第七章 复 数随堂演练一、复数的概念二、复数的几何意义三、复数的四则运算内容索引知识网络知识网络一、复数的概念1.复数的概念是掌握复数的基础,如虚数、纯虚数、复数相等、复数的模等.有关复数的题目不同于实数,应注意根据复数的相关概念解答.2.掌握复数的相关概念,培养数学抽象素养.例1 已知z=lg(m2-2m-2)+(m2+3m+2)i,试求实数m的取值,使(1)z是纯虚数;(2)z是实数;∴当m=3时,z是纯虚数.∴当m=-1或m=-2时,z是实数.(3)z在复平面内对应的点位于第二象限.反思感悟 处理复数概念问题的两个注意点(1)当复数不是a+bi(a,b∈R)的形式时,要通过变形化为a+bi的形式,以便确定其实部和虚部.(2)求解时,要注意实部和虚部本身对变量的要求,否则容易产生增根.A.0 B.-1 C.1 D.-2√(2)已知z1=m2-3m+m2i,z2=4+(5m+6)i,其中m为实数,i为虚数单位,若z1-z2=0,则m的值为A.4 B.-1 C.6 D.-1或6√解析 由题意可得z1=z2,即m2-3m+m2i=4+(5m+6)i,解得m=-1.二、复数的几何意义1.复数运算与复数几何意义的综合是高考常见的考查题型,解答此类问题的关键是利用复数运算将复数化为代数形式,再利用复数的几何意义解题.2.通过复数几何意义的学习,培养直观想象素养.A.第一象限 B.第二象限C.第三象限 D.第四象限√∴1-4i=2(2+3i)+(a+bi),-3-10反思感悟 在复平面内确定复数对应的点的步骤(1)由复数确定有序实数对,即z=a+bi(a,b∈R)确定有序实数对(a,b).(2)由有序实数对(a,b)确定复平面内的点Z(a,b).所以点D对应的复数为z=3+3i,三、复数的四则运算1.复数运算是本章的重要内容,是高考考查的重点和热点,每年高考都有考查,一般以复数的乘法和除法运算为主.2.借助复数运算的学习,提升数学运算素养.例3 计算:=-1+i-1=-2+i.(2)(4-i5)(6+2i7)+(7+i11)(4-3i).解 原式=(4-i)(6-2i)+(7-i)(4-3i)=22-14i+25-25i=47-39i.反思感悟 进行复数代数运算的策略(1)复数代数形式的运算的基本思路就是应用运算法则进行计算.(2)复数的四则运算中含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可,但要注意把i的幂写成最简单的形式.A.1+i或-2+i B.i或1+iC.i或-1+i D.-1-i或-2+i√解析 设z=a+bi(a,b∈R),所以b=1,a2+a+1=1,所以a=0或a=-1.故z=i或z=-1+i.A.i B.-i C.1+i D.1-i√解析 因为(1-i)2=1-2i+i2=-2i,=i50-i25+1=i2-i+1=-i.随堂演练A.1 B.-1 C.i D.-i√12342.下列各式的运算结果为纯虚数的是A.i(1+i)2 B.i2(1-i)C.(1+i)2 D.i(1+i)√1234解析 A项,i(1+i)2=i(1+2i+i2)=i×2i=-2,不是纯虚数;B项,i2(1-i)=-(1-i)=-1+i,不是纯虚数;C项,(1+i)2=1+2i+i2=2i,是纯虚数;D项,i(1+i)=i+i2=-1+i,不是纯虚数.3.设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则A.(x+1)2+y2=1 B.(x-1)2+y2=1C.x2+(y-1)2=1 D.x2+(y+1)2=1√1234解析 ∵z在复平面内对应的点为(x,y),∴z=x+yi(x,y∈R).∵|z-i|=1,∴|x+(y-1)i|=1,∴x2+(y-1)2=1.4.若z=1+i,则|z2-2z|等于1234解析 方法一 z2-2z=(1+i)2-2(1+i)=-2,|z2-2z|=|-2|=2.方法二 |z2-2z|=|(1+i)2-2(1+i)|=|(1+i)(-1+i)|=|1+i|·|-1+i|=2.√
高中数学新教材同步课件必修第二册 高考政策|高中“新”课程,新在哪里?1、科目变化:外语语种增加,体育与健康必修。第一,必修课程,由国家根据学生全面发展需要设置,所有学生必须全部修习、全部考试。第二,选择性必修课程,由国家根据学生个性发展和升学考试需要设置。第三,选修课程,由学校根据实际情况统筹规划开设,学生自主选择修习。2、课程类别变化,必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下,对原必修课程学分进行重构,由必修课程学分、选择性必修课程学分组成,适当增加选修课程学分。3、学时和学分变化,高中生全年假期缩减到11周。4、授课方式变化,选课制度将全面推开。5、考试方式变化,高考统考科目由教育部命题,学业水平合格性、等级性考试由各省命题。章末复习课第七章 复 数随堂演练一、复数的概念二、复数的几何意义三、复数的四则运算内容索引知识网络知识网络一、复数的概念1.复数的概念是掌握复数的基础,如虚数、纯虚数、复数相等、复数的模等.有关复数的题目不同于实数,应注意根据复数的相关概念解答.2.掌握复数的相关概念,培养数学抽象素养.例1 已知z=lg(m2-2m-2)+(m2+3m+2)i,试求实数m的取值,使(1)z是纯虚数;(2)z是实数;∴当m=3时,z是纯虚数.∴当m=-1或m=-2时,z是实数.(3)z在复平面内对应的点位于第二象限.反思感悟 处理复数概念问题的两个注意点(1)当复数不是a+bi(a,b∈R)的形式时,要通过变形化为a+bi的形式,以便确定其实部和虚部.(2)求解时,要注意实部和虚部本身对变量的要求,否则容易产生增根.A.0 B.-1 C.1 D.-2√(2)已知z1=m2-3m+m2i,z2=4+(5m+6)i,其中m为实数,i为虚数单位,若z1-z2=0,则m的值为A.4 B.-1 C.6 D.-1或6√解析 由题意可得z1=z2,即m2-3m+m2i=4+(5m+6)i,解得m=-1.二、复数的几何意义1.复数运算与复数几何意义的综合是高考常见的考查题型,解答此类问题的关键是利用复数运算将复数化为代数形式,再利用复数的几何意义解题.2.通过复数几何意义的学习,培养直观想象素养.A.第一象限 B.第二象限C.第三象限 D.第四象限√∴1-4i=2(2+3i)+(a+bi),-3-10反思感悟 在复平面内确定复数对应的点的步骤(1)由复数确定有序实数对,即z=a+bi(a,b∈R)确定有序实数对(a,b).(2)由有序实数对(a,b)确定复平面内的点Z(a,b).所以点D对应的复数为z=3+3i,三、复数的四则运算1.复数运算是本章的重要内容,是高考考查的重点和热点,每年高考都有考查,一般以复数的乘法和除法运算为主.2.借助复数运算的学习,提升数学运算素养.例3 计算:=-1+i-1=-2+i.(2)(4-i5)(6+2i7)+(7+i11)(4-3i).解 原式=(4-i)(6-2i)+(7-i)(4-3i)=22-14i+25-25i=47-39i.反思感悟 进行复数代数运算的策略(1)复数代数形式的运算的基本思路就是应用运算法则进行计算.(2)复数的四则运算中含有虚数单位i的看作一类同类项,不含i的看作另一类同类项,分别合并即可,但要注意把i的幂写成最简单的形式.A.1+i或-2+i B.i或1+iC.i或-1+i D.-1-i或-2+i√解析 设z=a+bi(a,b∈R),所以b=1,a2+a+1=1,所以a=0或a=-1.故z=i或z=-1+i.A.i B.-i C.1+i D.1-i√解析 因为(1-i)2=1-2i+i2=-2i,=i50-i25+1=i2-i+1=-i.随堂演练A.1 B.-1 C.i D.-i√12342.下列各式的运算结果为纯虚数的是A.i(1+i)2 B.i2(1-i)C.(1+i)2 D.i(1+i)√1234解析 A项,i(1+i)2=i(1+2i+i2)=i×2i=-2,不是纯虚数;B项,i2(1-i)=-(1-i)=-1+i,不是纯虚数;C项,(1+i)2=1+2i+i2=2i,是纯虚数;D项,i(1+i)=i+i2=-1+i,不是纯虚数.3.设复数z满足|z-i|=1,z在复平面内对应的点为(x,y),则A.(x+1)2+y2=1 B.(x-1)2+y2=1C.x2+(y-1)2=1 D.x2+(y+1)2=1√1234解析 ∵z在复平面内对应的点为(x,y),∴z=x+yi(x,y∈R).∵|z-i|=1,∴|x+(y-1)i|=1,∴x2+(y-1)2=1.4.若z=1+i,则|z2-2z|等于1234解析 方法一 z2-2z=(1+i)2-2(1+i)=-2,|z2-2z|=|-2|=2.方法二 |z2-2z|=|(1+i)2-2(1+i)|=|(1+i)(-1+i)|=|1+i|·|-1+i|=2.√
相关资料
更多









