泰安市泰山学院附属中学2022-2023学年度第一学期九年级数学期末试题和答案

2022～2023学年度第一学期期末质量检测

九年级数学试题

注意事项

1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，其中选择题36分，非选择题84分，满分120分，考试时间120分钟；

2.选择题选出答案后，用2B铅笔把答题卡上对应题目的正确答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案，答案写在试卷上无效；

3.数学考试不允许使用计算器，考试结束后，应将答题纸和答题卡一并交回。

  第Ⅰ卷（选择题  共36分）

一、选择题（本大题共12个小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求.）

­1.已知tanA= ，则锐角A满足(    )

A.00＜A＜300      B.300＜A＜450       C.450＜A＜600    D.600＜A＜900

2.下列图案中，任意选取一个图案，既是中心对称图形也是轴对称图形的概率为(    )

A．                 B．                 C．                 D．1

3.图中几何体是由六个相同的小正方体组合而成的，则从它左边看到的平面图形是(   )

A．            B．          C．      D．

4.已知一次函数y1＝kx＋b(k＜0)与反比例函数y2＝(m≠0)的图象相交于A，B两点，其横坐标分别是－1和3，当y1＞y2时，实数x的取值范围是(    )

A.x＜－1或0＜x＜3  B.－1＜x＜0或0＜x＜3  C.－1＜x＜0或x＞3   D.0＜x＜3

5.点A.C为半径是3的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为(     )

A.或2     B.或2       C.或2     D.或2

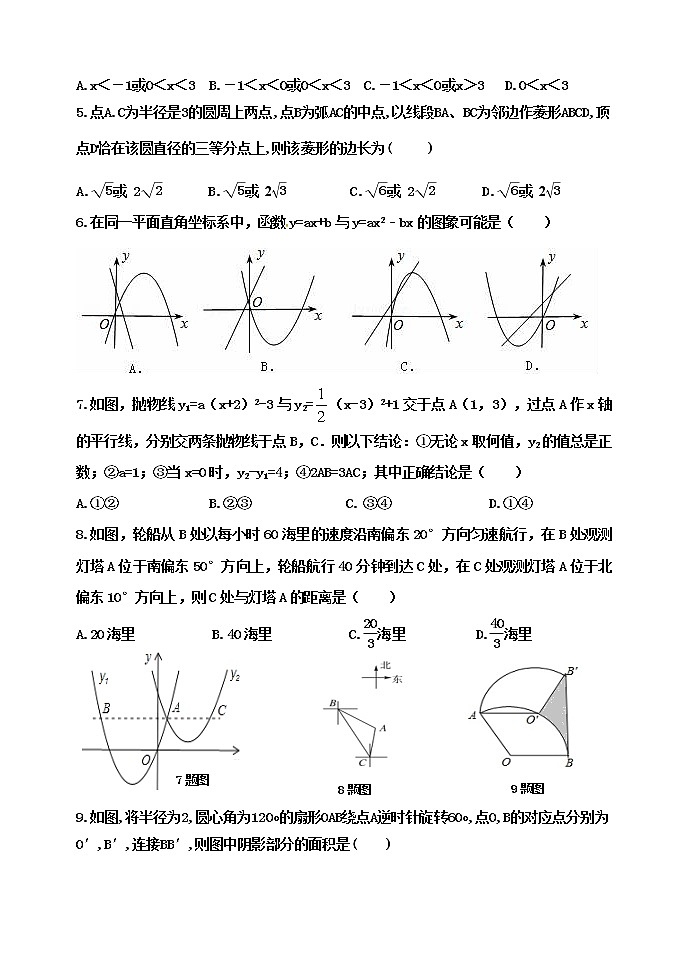
6.在同一平面直角坐标系中，函数y=ax+b与y=ax2﹣bx的图象可能是（    ）

7.如图，抛物线y1=a（x+2）2-3与y2=（x-3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，y2的值总是正数；②a=1；③当x=0时，y2-y1=4；④2AB=3AC；其中正确结论是（　　）

A.①②                          B.②③                          C. ③④                         D.①④

8.如图，轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行，在B处观测灯塔A位于南偏东50°方向上，轮船航行40分钟到达C处，在C处观测灯塔A位于北偏东10°方向上，则C处与灯塔A的距离是（    ）

A.20海里           B.40海里           C.海里          D.海里

9.如图,将半径为2,圆心角为120∘的扇形OAB绕点A逆时针旋转60∘,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是(    )

A.              B.2 -          C.2 -        D. 4 -

10.如图，O为坐标原点，四边形OACB是菱形，OB在x轴的正半轴上，sin∠AOB＝，反比例函数y＝在第一象限内的图象经过点A，与BC交于点F，则△AOF的面积等于(    )

A.60                B.80              C.30            D.40

11.已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为(    )

A.3或6              B.1或6            C.1或3           D.4或6

12.如图，在⊙O中,圆的半径为6，点B是圆上一动点，且∠ABD=30o,AC是⊙O的切线,则CD的最小值是(    )

A.1                   B.3                C.            D.2

2018～2019学年度第一学期期末质量检测

九年级数学试题

第Ⅱ卷（非选择题  共84分）

注意事项： 1.第Ⅱ卷共6页，用蓝黑钢笔或圆珠笔直接答在答题纸上；

2.答卷前将密封线内的项目填写清楚。

二、填空题（本大题共6个小题，每小题3分，共18分．把答案填在题中的横线上.）

13.如图,已知反比例函数y=(k为常数,k≠0)的图象经过点A，过A点作AB⊥x轴，垂足为B.若△AOB的面积为1，则k=_____.

14. 如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则tan∠AOD=      .

15.工人师傅用一张半径为24cm,圆心角为150o的扇形铁皮做成一个圆锥的侧面，则这个圆锥的高为        .

16.我国魏晋时期数学家刘徽首创“割圆术”计算圆周率。随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部。如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为        . (用含m,n的式子表示)   

17.已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有5个结论：①abc＞0；

②b＞a+c；③9a+3b+c＞0； ④c＜-3a； ⑤a+b≥m（am+b），其中正确的有是       .

18.如图，把n个边长为1的正方形拼接成一排，求得tan∠BA1C=1，tan∠BA2C=，

tan∠BA3C=,按此规律写出tan∠BAnC=       （用含n的代数式表示）      

三、解答题（本大题共7个小题，共66分，解答应写出文字说明、推理过程或演算步骤。）

19.(本题满分共8分)

已知一次函数y1=x+m的图象与反比例函数y2= 的图象交于A、B两点．已知当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．

求：（1）求一次函数的解析式；
（2）已知双曲线在第一象限的图像上有一点C到y轴的距离为3，求△ABC的面积．

20.（本题满分共8分）

如图，测量人员在山脚A处测得山顶B的仰角为450，沿着仰角为300的山坡前进1000米到达D处，在D处测得山顶B的仰角为600，

DE⊥BC，求山的高度(结果保留根号).

21. (本题满分共9分)

“泰安市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：

(1)接受问卷调查的学生共有___人，扇形统计图中“基本了解”部分所对应扇形的圆心角为___；

(2)请补全条形统计图；

(3)若该中学共有学生900人，请根据

上述调查结果，估计该中学学生中对校园

安全知识达到“了解”和“基本了解”

程度的总人数；

(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.

22. (本题满分共9分)

某商场经营某种品牌的童装，购进时的单价是40元．根据市场调查，在一段时间内，销售单价是60元时，销售量是100件，而销售单价每降低1元，就可多售出10件．
（1）写出销售量y（件）与销售单价x（元）之间的函数关系式；
（2）写出销售该品牌童装获得的利润w（元）与销售单价x（元）之间的函数关系式；
（3）若童装厂规定该品牌童装销售单价不低于56元，且商场要完成不少于110件的销售任务，则商场销售该品牌童装获得的最大利润是多少元？

23. (本题满分共10分)

矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y=（k＞0）的图象与边AC交于点E．

（1）当点F运动到边BC的中点时，求点E的坐标；

（2）连接EF，求∠EFC的正切值；

（3）如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式．

24.(本题满分共10分)

如图，四边形ABCD中，AB=AD=CD，以AB为直径⊙O的经过点C，连接AC、OD交于点E.

（1）证明：OD∥BC；

（2）若tan∠ABC=2，证明：DA与⊙O相切；

（3）在（2）条件下，连接BD交⊙O于点F，连接EF，若BC=1，求EF的长.

25. (本题满分共12分)

如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.

(1)求抛物线的解析式；

(2)当0＜t≤8时，求△APC面积的最大值；

(3)当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似?若存在，求出此时t的值；若不存在，请说明理由.

2022～2023学年度第一学期九年级期末质量检测

  九年级数学参考答案

阅卷须知：

1.为便于阅卷，本试卷答案中有关解答题的推导步骤写得较为详细，阅卷时，只要考生将主要过程正确写出即可；

2.若考生的解法与给出的解法不同，正确者相应给分；

一、选择题（本大题共12个小题，每小题3分，共36分．）

二、填空题（本大题共6个小题，每小题3分，共12分。）

13.-2    14. 2  15.2cm     16.    17. ②④⑤    18.

三、解答题

19．解：（1）∵当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2，∴点A的横坐标为1，

代入反比例函数解析式， 解得y=6，∴点A的坐标为（1，6），

又∵点A在一次函数图象上，∴1+m=6，解得m=5，

∴一次函数的解析式为y1=x+5；

（2）∵第一象限内点C到y轴的距离为3，∴点C的横坐标为3，

∴y=2，∴点C的坐标为（3，2），过点C作CD∥x轴交直线AB于D，

则点D的纵坐标为2，∴x+5=2，解得x= -3，∴点D的坐标为（-3，2），

∴CD=3-（-3）=3+3=6，点A到CD的距离为6-2=4，

由y=和y=x+5解得x=1（舍去）∴x=-6∴点B的坐标为（-6，-1），

∴点B到CD的距离为2-（-1）=2+1=3，S△ABC=S△ACD+S△BCD=×6×4+ ×6×3=12+9=21

20.解：∵∠BAC=450，∠DAC=300，∴∠BAD=150，∵∠BDE=600，∠BED=900，∴∠DBE=300，

∵∠ABC=450，∴∠ABD=150，∴∠ABD=∠DAB，∴AD=BD=1000，过点D作DF⊥AC，∵AC⊥BC，DF⊥AC，DE⊥BC，∴∠DFC=∠ACB=∠DEC=90∘∴四边形DFCE是矩形  ∴DF=CE，

在直角三角ADF中，∵∠DAF=30∘，∴DF=AD=500，∴EC=500，

在直角三角BDE中，BE=1000×sin60∘=500．

∴BC=500+500(米.)∴山的高度是（500+500） 米.

21.解：(1)∵了解很少的有30人，占50%，∴接受问卷调查的学生共有：30÷50%=60(人)；

∴扇形统计图中“基本了解”部分所对应扇形的圆心角为：15÷60×3600=900；故答案为：60,900；

(2)60−15−30−10=5(人)；补全条形统计图得：

(3)根据题意得：900×(15+5)÷60=300(人)，

则估计该中学学生中对校园安全知识达到“了解”和

“基本了解”程度的总人数为300人；

(4)画树状图得：

∵共有20种等可能的结果，恰好抽到1个男生和1个女生的有12种情况，

∴恰好抽到1个男生和1个女生的概率为：=

22解（1）由题意得：y= -10x+700，故销售量y件与销售单价x元之间的函数关系式为y= -10x+700；
（2）由题意，得：w=（x-40）(-10x+700）= -10x2+1100x-28000，

答：W与x之间的函数关系式是w= -10x2+1100x-28000；
（3）由题意，得：-10x+700≥110    x≥56    解得56≤x≤59，W= -10x2+1100x-28000= -10（x-55）2+2250，对称轴为直线x＝55，又∵a＜0，56≤x≤59在对称轴右侧，w随x增大而减小．
∴当x=56时，W最大=（56-40）(-10×56+700）=2240．答：这段时间商场最多获利2240元．

23. 解：（1）∵OA=3，OB=4，∴B（4，0），C（4，3），∵F是BC的中点，∴F（4，），

∵F在反比例y=函数图象上，∴k=4×=6，∴反比例函数的解析式为y=，∵E点的坐标为3，

∴E（2，3）；

（2）∵F点的横坐标为4，∴F（4，），∴CF=BC﹣BF=3﹣=∵E的纵坐标为3，

∴E（，3），∴CE=AC﹣AE=4﹣=，在Rt△CEF中，tan∠EFC=，

（3）如图，过点E作EH⊥OB于H，由（2）知，CF=，CE=，CE：CF=4：3，

∴EH=OA=3，∠EHG=∠GBF=90°，∴∠EGH+∠HEG=90°，

由折叠知，EG=CE，FG=CF，∠EGF=∠C=90°，

∴∠EGH+∠BGF=90°，∴∠HEG=∠BGF，∵∠EHG=∠GBF=90°，

∴△EHG∽△GBF，∴=，∴，∴BG=，

在Rt△FBG中，FG2﹣BF2=BG2，

∴（）2﹣（）2=，∴k=，∴反比例函数解析式为y=． 

24.(1)                 (2)

(3)

25.(1) 由题意知x1、x2是方程mx2−8mx+4m+2=0的两根，∴x1+x2=8，又x2−x1=4

∴x1=2  x2=6∴B(2,0)、C(6,0)则4m−16m+4m+2=0，解得：m=  ∴该抛物线解析式为：y=x2−2x+3；

(2) 可求得A(0,3) C(6,0)设直线AC的解析式为：y=kx+b，

解得k=− b=3∴直线AC的解析式为：y=− x+3，

要构成△APC，显然t≠6，分两种情况讨论：

∵P(t, t2−2t+3),∴PF=−t2+t，

∴S△APC= (− t2+t)×6=−(t−3)2+，此时最大值为：

②当6<t≤8时,设直线l与AC交点为M,则：M(t,− t+3)，∵P(t, t2−2t+3),∴PM=t2−t，

∴S△APC= (t2− t)×6=(t−3)2-，当t=8时，取最大值，最大值为：12，

综上可知，当0<t≤8时，△APC面积的最大值为12；

(3) 如图,连接AB,则△AOB中,∠AOB=900，AO=3，BO=2，Q(t,3),P(t, t2−2t+3)，

①当2<t<8时,AQ=t,PQ= - t2+2t，

若：△AOB∽△AQP,则：AO︰AQ=BO︰PQ，即：3︰t=2︰(- t2+2t)，∴t=0(舍),或t=

若△AOB∽△PQA,则：AO︰PQ=OB︰AQ，即：3︰(- t2+2t)=2︰t，∴t=0(舍)或t=2(舍)，

②当t>8时,AQ′=t,PQ′=t2−2t，

若：△AOB∽△AQP,则：AO︰AQ′=BO︰P′Q′，即：3︰t=2︰(t2−2t)，∴t=0(舍),或t=，

若△AOB∽△PQA,则：AO︰P′Q′=BO︰AQ′，即：2︰t=3︰(t2−2t)，∴t=0(舍)或t=14，

∴t=或t=或t=14.