数学（福建专用A卷）-学易金卷：2022-2023学年七年级下学期期中考前必刷卷

这是一份数学（福建专用A卷）-学易金卷：2022-2023学年七年级下学期期中考前必刷卷，文件包含数学福建专用A卷-全解全析docx、数学福建专用A卷-参考答案docx、数学福建专用A卷-考试版A4docx、数学福建专用A卷-考试版A3docx等4份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

学易金卷：2022-2023学年七年级下学期期中考前必刷卷
数学·全解全析（福建专用A卷：提升卷）
一、选择题（本大题共10小题，每小题4分，共34分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）
1．（西藏林芝市广东实验中学2021-2022学年七年级下学期期中考试数学试题）如图所示的车标，可以看作由平移得到的是（       ）
A． B． C． D．
【答案】B
【分析】根据平移的定义结合图形进行判断．
【详解】解：根据平移的定义可知，只有B选项是由一个圆作为基本图形，经过平移得到．
故选：B．
【点睛】本题考查了平移的定义：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，图形的这种移动叫做平移．解题的关键是注意平移是图形整体沿某一直线方向移动，平移不改变图形的形状和大小．
2．（黑龙江省哈尔滨市松北区顺迈学校2022-2023学年七年级上学期12月份阶段数学（五四制）学科试卷）在平面直角坐标系中，A−2,6在第（    ）象限
A．一 B．二 C．三 D．四
【答案】B
【分析】根据各象限内点的坐标符号特征即可得到答案．
【详解】解：∵−2<0，6>0，
∴A−2,6在第二象限，
故选B．
【点睛】本题考查了点的坐标，解题关键是掌握各象限内点的坐标符号特征：第一象限+,+，第二象限−,+，第三象限−,−，第四象限+,−．
3．（福建省莆田市荔城区2022-2023年七年级下学期数学期中考试卷）下列各数：π2，0，9，0.2，227，0.303003⋯（相邻两个3之间依次多一个0），1−2中，无理数的个数为（    ）
A．2个 B．3个 C．4个 D．5个
【答案】B
【分析】根据无理数的定义求解即可．
【详解】π2是无理数，0是有理数，9=3是有理数，0.2是有理数，227是有理数，0.303003⋯（相邻两个3之间依次多一个0）是无理数，1−2是无理数，
故无理数的个数有3个，
故选：B．
【点睛】此题主要考查了无理数的定义：无限不循环的小数为无理数，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.303003⋯（相邻两个3之间依次多一个0），等有这样规律的数．
4．（河南省南阳市镇平县2022-2023学年八年级上学期期末数学试题）已知实数a的一个平方根是2，则它的另一个平方根是（    ）
A．−2 B．−2 C．−4 D．±2
【答案】A
【分析】根据一个正数的平方根有两个，互为相反数，进行判断即可．
【详解】解：∵实数a的一个平方根是2，
∴a=4，
又∵一个正数的平方根有两个，互为相反数，
∴它的另一个平方根是：−2；
故选A．
【点睛】本题考查平方根的性质．熟练掌握，一个正数的平方根有两个，互为相反数，是解题的关键．
5．（福建省福州时代中学2021-2022学年七年级下学期期中考数学试卷）如图，直线l1⊥l2，在某平面直角坐标系中，x轴∥l2，y轴∥l1，点A的坐标为(2,3)，点B的坐标为(−4,−1)，则点C所在象限是（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限
【答案】B
【分析】先根据点A的坐标为(2,3)，点B的坐标为(−4,−1)，结合x轴∥l2，y轴∥l1，建立平面直角坐标系，即可判断出点C所在的象限．
【详解】解：如图，
，
∵点A的坐标为(2,3)，点B的坐标为(−4,−1)，
∴点A位于第一象限，点B位于第三象限，
∵x轴∥l2，y轴∥l1，
∴建立如图所示的平面直角坐标系，
∴点C位于第二象限，故B正确．
故选：B．
【点睛】本题主要考查了平面直角坐标系中各象限内点的坐标特征，解题的关键是根据题意建立平面直角坐标系，利用“数形结合”的数学思想解决问题．
6．（福建省福州第十一中学2021-2022学年七年级下学期期中数学试卷）下列命题是真命题的是（    ）
A．同位角相等
B．两个锐角的和是锐角
C．若两个角的和为180°，则这两个角互补
D．相等的角是对顶角
【答案】C
【分析】根据平行线的性质，补角的定义，锐角的定义，对顶角的定义逐项进行判断即可．
【详解】解：A、两直线平行，同位角相等，故原命题错误，是假命题，不符合题意；
B、两个锐角的和可能是锐角、钝角，也可能是直角，故原命题错误，是假命题，不符合题意；
C、若两个角的和为180°，则这两个角互补，正确，是真命题，符合题意；
D、相等的角不一定是对顶角，故原命题错误，是假命题，不符合题意．
故选：C．
【点睛】本题主要考查了命题真假的判定，解题的关键是熟练掌握平行线的性质，补角的定义，锐角的定义，对顶角的定义．
7．（福建省龙岩市新罗区雁石中学2021-2022学年七年级数学下学期第一次月考测试题）如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

A．∠3=∠4 B．∠D+∠ACD=180°
C．∠D=∠DCE D．∠1=∠2
【答案】D
【分析】根据平行线的判定条件逐一判断即可．
【详解】解：A、由∠3=∠4可根据内错角相等，两直线平行判断DB∥AC ，不能判断AB∥CD，故此选项不符合题意；
B、由∠D+∠ACD=180°可根据同旁内角互补，两直线平行判断DB∥AC ，不能判断AB∥CD，故此选项不符合题意；
C、由∠D=∠DCE可根据内错角相等，两直线平行判断DB∥AC ，不能判断AB∥CD，故此选项不符合题意；
D、由∠1=∠2可根据内错角相等，两直线平行判断AB∥CD，故此选项符合题意；
故选：D．
【点睛】本题主要考查了平行线的判定，熟知平行线的判定条件是解题的关键．
8．（北京市第十九中学2021-2022学年七年级下学期期中考试数学试卷）直线AB，CD相交于点O．OE，OF，OG分别平分∠AOC，∠BOC，∠AOD．下列说法正确的是(　　)
A．OE，OF在同一直线上 B．OE，OG在同一直线上
C．OG⊥OF D．OE⊥OF
【答案】D
【分析】根据角平分线的性质得到∠COE=12∠AOC，∠COF=12∠BOC，又因为∠AOC与∠BOC是补角，所以∠COE+∠COF=90°，所以OE⊥OF，所以A错误，D正确；因为∠AOG=12∠AOD，且∠AOD与∠BOC是对顶角，所以∠AOG=∠BOF，所以，OF与OG共线，所以，OE⊥OG，所以B，C均错误．
【详解】解：如图，

∵∠AOC=∠BOD，
∵OE，OF分别是∠AOC，∠BOC的平分线，
∴∠COE=12∠AOC，∠COF=∠BOF=12∠BOC，
∵OG是∠AOD的平分线，
∴∠AOG=∠DOG，
∴∠COE+∠COF=∠AOE+∠BOF=12×180°=90°，
∴∠EOG=∠FOE=90°，
∴射线OE，OF互相垂直，故D正确；故A错误；射线OF，OG互相垂直；故C错误；故B错误．
故选：D．
【点睛】本题考查了垂线，对顶角，角平分线的定义，正确的识别图形是解题的关键．
9．（福建省泉州市台商投资区2022-2023学年七年级上学期期中质量检测数学试题）定义：a是不为1的有理数，我们把11−a称为a的差倒数，如2的差倒数是11−2=−1．现已知a1=−2，a2是a1的差倒数，a3是a2的差倒数，…，以此类推，则a2022的值为（　　）
A．-2 B．−12 C．13 D．32
【答案】D
【分析】根据差倒数的定义分别计算出a1，a2，a3，a4···，进而得到循环规律，再求值即可．
【详解】解：∵a1=−2，
a2=11−(−2)=13，
a3=11−13=32，
a4=11−32=−2，
a5=11−−2=13，
···
∴这列数是三个数依次不断循环出现.
∵2022÷3=674，
∴a2022=a3=32．
故选：D．
【点睛】本题主要考查了新定义，数字的变化规律，根据新定义的理解得出数字变化规律是解题的关键．
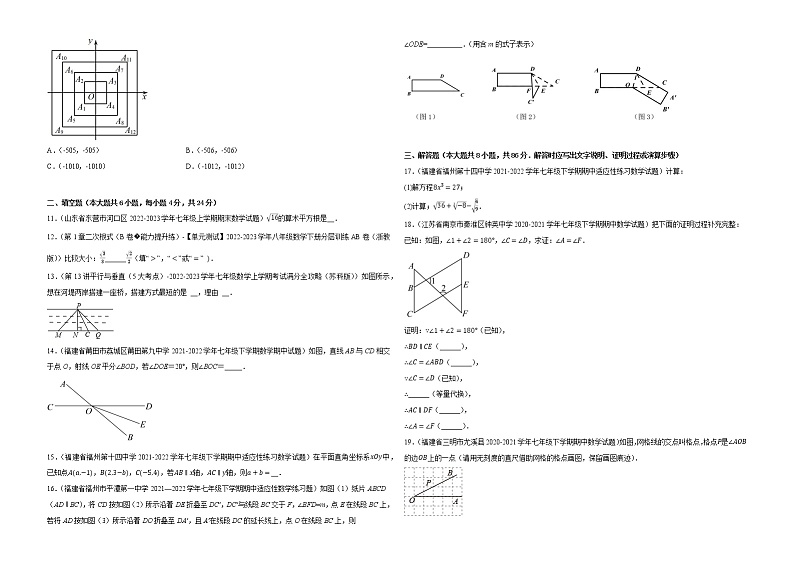
10．（福建省莆田市荔城区莆田第九中学2021-2022学年七年级下学期数学期中试题）如图，正方形A1A2A3A4、A5A6A7A8、A9A10A11A12、…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A1，A2，A3，A4，A5，A6，A7，A8，A9，A10，A11，A12，……）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6，……，则顶点A2021的坐标为（　　）

A．（-505，-505） B．（-506，-506）
C．（-1010，-1010） D．（-1012，-1012）
【答案】B
【分析】观察图形，由第四象限点的坐标的变化可得出“点A4n的坐标为（n，-n）（n为正整数）”，再结合2020=4×505，据此即可求出点A2021的坐标．
【详解】解：观察图形，可知：点A4的坐标为（1，-1），点A8的坐标为（2，-2），点A12的坐标为（3，-3），…，
∴点A4n的坐标为（n，-n）（n为正整数）．
又∵2020=4×505，
∴点A2020的坐标为（505，-505）．
∴点A2021的坐标为（-506，-506）．
故选：B．
【点睛】本题考查了规律型：点的坐标，由第四象限点的坐标的变化找出变化规律“点A4n的坐标为（n，-n）（n为正整数）”是解题的关键．
二、填空题（本大题共6小题，每小题4分，共24分）
11．（山东省东营市河口区2022-2023学年七年级上学期期末数学试题）16的算术平方根是__．
【答案】2
【分析】根据算术平方根的运算法则，直接计算即可．
【详解】解：∵16=4，4的算术平方根是2，
∴16的算术平方根是2．
故答案为：2．
【点睛】此题考查了求一个数的算术平方根，这里需注意：16的算术平方根和16的算术平方根是完全不一样的；因此求一个式子的平方根、立方根和算术平方根时，通常需先将式子化简，然后再去求，避免出错．
12．（第1章二次根式（B卷�能力提升练）-【单元测试】2022-2023学年八年级数学下册分层训练AB卷（浙教版））比较大小：33______22（填“>”，“<”或“=” )．
【答案】<
【分析】根据实数的大小比较的方法，先将两个无理数平方，根据正数平方越大，原实数就越大即可得．
【详解】解：∵332=13，(22)2=12，
∴13<12，
∴33<22，
故答案为：<．
【点睛】本题考查了实数的大小比较，灵活运用平方将无理数转化为可比较大小的有理数是解题的关键．
13．（第13讲平行与垂直（5大考点）-2022-2023学年七年级数学上学期考试满分全攻略（苏科版））如图所示，想在河堤两岸搭建一座桥，搭建方式最短的是 __，理由 __．

【答案】     PN     垂线段最短
【分析】根据从直线外一点到这条直线上各点所连的线段中，垂线段最短.可知搭建方式最短的是PN，理由垂线段最短．
【详解】解：因为PN⊥MQ，垂足为N，则PN为垂线段，根据垂线段最短，
故填空为：PN，垂线段最短．
【点评】此题主要考查了从直线外一点到这条直线上各点所连的线段中，垂线段最短在生活中的应用．解决本题的关键是熟练掌握垂线段最短的应用．
14．（福建省莆田市荔城区莆田第九中学2021-2022学年七年级下学期数学期中试题）如图，直线AB与CD相交于点O，射线OE平分∠BOD，若∠DOE＝20°，则∠BOC＝_____．

【答案】140°##140度

【分析】根据角平分线的性质求出∠DOB＝40°，再根据邻补角的定义即可得出∠BOC的度数．
【详解】解：∵射线OE平分∠BOD，若∠DOE＝20°，
∴∠BOD＝2∠DOE ＝40°，
∴∠BOC＝180°−∠BOD＝180°−40°=140°．
故答案为：140°
【点睛】本题考查了角平分线和邻补角，熟记角平分线性质和邻补角定义是解决本题的关键．
15．（福建省福州第十四中学2021-2022学年七年级下学期期中适应性练习数学试题）在平面直角坐标系xOy中，已知点A(a,−1)，B(2,3−b)，C(−5,4)，若AB∥x轴，AC∥y轴，则a+b=__．
【答案】−1
【分析】根据平行于x轴的直线上所有点的纵坐标相等，平行于y轴的直线上所有点的横坐标相等计算即可；
【详解】解：∵A(a,−1)，B(2,3−b)，C(−5,4)．AB∥x轴，AC∥y轴，
∴−1=3−b且a=−5，
∴b=4，
∴a+b=−5+4=−1；
故答案为：−1．
【点睛】本题主要考查了平面直角坐标系中平行于坐标轴的直线上点的特征和代数式求值，准确计算是解题的关键．
16．（福建省福州市平潭第一中学2021—2022学年七年级下学期期中适应性数学练习题）如图（1）纸片ABCD（AD∥BC），将CD按如图（2）所示沿着DE折叠至DC′，DC′与线段BC交于F，∠BFD=m，点E在线段BC上，若将AD按如图（3）所示沿着DO折叠至DA′，且A′在线段DC的延长线上，点O在线段BC上，则∠ODE=__________．（用含m的式子表示）

【答案】90°−12m
【分析】设∠CDE=x，∠DCE=y，由图（1）折叠性质可得：∠C’DE=∠CDE=x，由平行线性质可得∠ADF=180°-m，则∠ADC=180°-m+2x，由图（2）折叠性质可得：∠ADO=∠CDO=12∠ADC=90°−12m+x，最后可得∠ODE的度数．
【详解】解：设∠CDE=x，∠DCE=y，
由图（1）折叠性质可得：∠C’DE=∠CDE=x，
∵∠BFD=m，AD∥BC，
∴∠BFD+∠ADF=180°，
∴∠ADF=180°-m，
∴∠ADC=180°-m+2x，
由图（2）折叠性质可得：∠ADO=∠CDO=12∠ADC=180°−m+2x2=90°−12m+x，
∴∠ODE=∠CDO-∠CDE=90°−12m+x−x=90°−12m．
故答案为：90°−12m．
【点睛】本题考查了平行线的性质及角的有关计算，解决本题的关键是熟练掌握平行线的性质．
三、解答题（本大题共8小题，共86分．解答时应写出文字说明、证明过程或演算步骤）
17．（福建省福州第十四中学2021-2022学年七年级下学期期中适应性练习数学试题）计算：
(1)解方程8x3=27；
(2)计算；36+3−8−49．
【答案】(1)x=32
(2)103

【分析】（1）利用立方根的意义解答即可；
（2）利用算术平方根和立方根的意义解答即可；
【详解】（1）解：∵8x3=27，
∴x3=278，
∴x=32；
（2）解：原式=6−2−23
=4−23
=103．
【点睛】本题主要考查了实数的运算，算术平方根和立方根的意义，正确利用算术平方根和立方根的意义解答是解题的关键．
18．（江苏省南京市秦淮区钟英中学2020-2021学年七年级下学期期中数学试题）把下面的证明过程补充完整：
已知：如图，∠1+∠2=180°，∠C=∠D，求证：∠A=∠F．

证明：∵∠1+∠2=180°（已知），
∴BD∥CE（______），
∴∠C=∠ABD（______），
∵∠C=∠D（已知），
∴______（等量代换），
∴AC∥DF（______），
∴∠A=∠F（______）．
【答案】同旁内角互补，两直线平行；两直线平行，同位角相等；∠ABD=∠D；内错角相等，两直线平行；两直线平行，内错角相等
【分析】根据平行线的性质与判定定理，结合图形完成填空即可求解．
【详解】证明：∵∠1+∠2=180°（已知），
∴BD∥CE（同旁内角互补，两直线平行），
∴∠C=∠ABD（两直线平行，同位角相等），
∵∠C=∠D（已知），
∴∠ABD=∠D（等量代换），
∴AC∥DF（内错角相等，两直线平行），
∴∠A=∠F（两直线平行，内错角相等）．
故答案为：同旁内角互补，两直线平行；两直线平行，同位角相等；∠ABD=∠D；内错角相等，两直线平行；两直线平行，内错角相等．
【点睛】本题考查了平行线的性质与判定，掌握平行线的性质与判定是解题的关键．
19．（福建省三明市尤溪县2020-2021学年七年级下学期期中数学试题）如图，网格线的交点叫格点，格点P是∠AOB的边OB上的一点（请用无刻度的直尺借助网格的格点画图，保留画图痕迹）．

（1）过点P画OB的垂线，交OA于点E；过点P画OA的垂线，垂足为F；
（2）线段PF的长度是点P到____________的距离，线段___________的长度是点E到直线OB的距离，所以线段PE、PF、OE这三条线段大小关系是_______________（用“<”号连接），理由是________________________________；
（3）写出图中∠AOB的余角是__________________________（不再标注其它字母）．
【答案】（1）见解析；（2）直线OA，PE，PF 【分析】（1）过点P画OB的垂线，作图即可；
（2）根据点到线的距离垂线段最短即可求解；
（3）根据余角的性质即可求解；
【详解】解：（1）如图，

画出PE，标注点E；
画出PF，标注点F；
（2）直线OA，PE，PF （3）∵∠EPO=90°，
∴∠AOB+∠OEP=90°，
∵∠PFO=90°，
∴∠OPF+∠AOB=90°，
故答案为：∠OEP和∠OPF．
【点睛】本题考查的是作图-简单作图，熟知垂线段的作法和余角的定义是解答此题的关键．
20．（福建省龙岩市武平县第三中学2021-2022学年七年级下学期期中数学试题）在平面直角坐标系中，已知点P(x，5x−3).
(1)若点P在x轴上，求点P的坐标．
(2)若点P到两坐标轴的距离相等，求点P的坐标．
【答案】(1)P(35，0)
(2)P(34，34)或P(12，−12)

【分析】（1）根据x轴上点的特征进行解答，即可得出答案；
（2）由P到两坐标轴的距离相等的点横纵坐标绝对值相等，列出方程，即可得出答案．
(1)
解：∵点P在x轴上，
∴5x−3=0，
∴x=35，
∴ P(35，0) ．
(2)
∵点P到两坐标轴的距离相等，
∴|x|=|5x−3|，
∴x=5x−3或x=−(5x−3)，
∴x=34或x=12，
∴ P(34，34)或P(12，−12)．
【点睛】本题考查了根据点的特征列出方程，求出点的坐标，掌握根据点的特征列出方程是解题的关键．
21．（广东省佛山市南海实验中学2022-2023学年八年级上学期第一次调研数学试卷）已知正实数x的平方根是m和m+n.
(1)当n=6时，求m的值；
(2)若m2x+(m+n)2x=32，求x的值.
【答案】(1)m=−3
(2)x=4

【分析】（1）利用正实数平方根互为相反数即可求出m的值；
（2）利用平方根的定义得到(m+n)2=x，m2=x，代入式子m2x+(m+n)2x=32即可求出x值．
【详解】（1）∵正实数x的平方根是m和m+n，
∴m+m+n=0，
∵n=6，
∴2m+6=0，
∴m=−3；
（2）∵正实数x的平方根是m和m+n，
∴(m+n)2=x，m2=x，
∵m2x+(m+n)2x=32，
∴x2+x2=32，
∴x2=16，
∵x＞0，
∴x=4．
【点睛】本题考查了平方根的定义及平方根的性质，熟练掌握这两个知识点是解题的关键．
22．（福建省三明市梅列区2020-2021学年七年级上学期期末数学试题）如图，直线AB，CD相交于点O，OE平分∠BOD．

（1）若∠BOD=70°，∠DOF=90°．则∠EOF=_______°；
（2）若OF平分∠COE，∠DOE=40°，求∠BOF的度数．
【答案】（1）55；（2）30°
【分析】（1）依据角平分线的定义以及角的和差，即可得到∠BOE的度数；
（2）依据OE平分∠BOD可以得到∠BOE＝∠DOE＝40°，∠BOD＝80°，进而可求得∠COE＝140°，再根据OF平分∠COE可得到∠EOF＝70°，最后根据∠BOF＝∠EOF－∠BOE即可求得答案．
【详解】解：（1）∵∠BOD＝70°，OE平分∠BOD，
∴∠DOE＝12∠BOD＝35°，
又∵∠DOF＝90°，
∴∠EOF＝∠DOF－∠DOE＝55°，
故答案为：55；
（2）∵OE平分∠BOD，∠DOE＝40°，
∴∠BOE＝∠DOE＝40°，∠BOD＝2∠DOE＝80°，
∴∠COE＝180°－∠DOE
＝180°－40°
＝140°，
又∵OF平分∠COE，
∴∠EOF＝12∠COE＝70°，
∴∠BOF＝∠EOF－∠BOE
＝70°－40°
＝30°．
【点睛】此题主要考查了角的计算，以及角平分线和邻补角的定义，解决本题的关键是理清图形中角的关系．
23．（安徽省芜湖市镜湖区第二十九中学2021-2022学年七年级下学期期中考试数学试题）在平面直角坐标系中，已知点A(x,y)，点B(x−my,mx−y)（其中m为常数，且m≠0），则称B是点A的“m族衍生点”．例如：点A(1,2)的“3族衍生点”B的坐标为(1−3×2,3×1−2)，即B(−5,1)．
(1)点(2,0)的“2族衍生点”的坐标为_____________；
(2)若点A(x,0)（其中x≠0），点A的“m族衍生点”为点B，且AB=OA，求m的值；
(3)若点A(x,y)的“m族衍生点”与“−m族衍生点”关于y轴对称，则点A的位置在___________上．
【答案】(1)(2,4)
(2)m=±1
(3)y轴

【分析】（1）利用“m族衍生点”的定义求解；
（2）求出点B的坐标，利用AB=OA建立方程，然后求解；
（3）先求出点A的“m族衍生点”与“−m族衍生点”，再利用平面直角坐标系中坐标的对称变换求解．
（1）
解：点(2,0)的“2族衍生点”为(2−2×0,2×2−0)，即(2,4)．
（2）
解：点A(x,0)的“m族衍生点”为B(x−m×0,mx−0)，即B(x,mx)．
AB=mx，OA=x，
由AB=OA，得mx=x，
∴ m=±1．
（3）
解：点A(x,y)的“m族衍生点”为(x−my,mx−y)，“−m族衍生点”为(x+my,−mx−y)．
∵点A(x,y)的“m族衍生点”与“−m族衍生点”关于y轴对称，
∴ x−my=−(x+my)mx−y=−mx−y，解得x=0，
∴点A(x,y)在y轴上．
【点睛】本题考查了平面直角坐标系中的新定义运算，平面直角坐标系中的轴对称，解决本题的关键是理解“新定义”所表达的内容，并熟练掌握平面直角坐标系相关知识．
24．（福建省三明市明溪县2021-2022学年七年级下学期期中数学试题）已知：如图，点B，C在线段AD的异侧，点E，F分别是线段AB，CD上的点，∠AEG=∠AGE，∠C=∠DGC．

(1)试说明：AB∥CD；
(2)如果∠AGE+∠AHF=180°，那么∠B=∠C吗?请说明理由；
(3)在（2）的条件下，若∠BFC-20°=3∠C，求∠AHB的度数．
【答案】(1)见解析
(2)∠B=∠C，理由见解析
(3)∠AHB=40°．

【分析】（1）由对顶角相等可得∠AGE=∠DGC，从而可得∠AEG=∠C，则可判定AB∥CD；
（2）由平角的定义可得∠AGE+∠EGH=180°，从而可求得∠EGH=∠AHF，则可判定EC∥BF，则有∠B=∠AEG，从而可求证；
（3）由（2）得BF∥EC，则有∠BFC+∠C=180°，从而可求∠C的度数，再利用平行线的性质即可求∠AHB的度数．
【详解】（1）证明：∵∠AEG=∠AGE，∠C=∠DGC，∠AGE=∠DGC，
∴∠AEG=∠C，
∴AB∥CD；
（2）证明：∵∠AGE+∠EGH=180°，∠AGE+∠AHF=180°，
∴∠EGH=∠AHF，
∴EC∥BF，
∴∠B=∠AEG，
∵AB∥CD，
∴∠C=∠AEG，
∴∠B=∠C；
（3）解：∵∠BFC-20°=3∠C，
∴∠BFC=3∠C+20°，
∵EC∥BF，
∴∠BFC+∠C=180°，
∴3∠C+20°+∠C=180°，
∴∠C=40°，
∴∠AEG=∠C=40°，
∴∠AGE=∠AEG=40°，
∵EC∥BF，
∴∠AHB=∠AGE=40°．
【点睛】本题主要考查平行线的判定与性质，解答的关键是结合图形分析清楚角之间的关系．
25．（福建省福州市福州现代中学2021-2022学年七年级下学期期中数学试题）在平面直角坐标系中，点A（a，1），B（b，3）满足关系式（a＋1）2＋b−2＝0

(1)求a、b的值；
(2)若点P（3，n）满足△ABP的面积等于6，求n的值；
(3)线段AB与y轴交于点C，动点E从点C出发，在y轴上以每秒1个单位长度的速度向下运动，动点F从点M（﹣8，0）出发，以每秒2个单位长度的速度向右运动，问t为何值时有S△ABE＝2S△ABF？求t的值．
【答案】(1)a=-1，b=2
(2)n=233或−13
(3)t=225或2

【分析】（1）利用偶次方的非负性及算术平方根的非负性得到a+1=0，b-2=0，由此求出a，b；
（2）过P作直线l⊥x轴，延长AB交直线l于点Q，设Q的坐标为（3，m），过A作AH⊥l交直线l于点H，利用S△AHQ=S△ABH+S△BQH，列式计算求出m=113，得到Q（3，113），再根据S△ABP=S△AQP−S△BPQ=12×PQ×3+1−12×PQ×3−2=32PQ，△ABP的面积等于6，列得32n−113=6，求出n；
（3）延长BA交x轴于D，过A作AG⊥x轴于G，过B作BN⊥x轴于N，根据S梯形AGOC+S梯形CONB=S梯形AGNB求出OC=53，由S△ADG+S梯形AGNB=S△DNB求出DG=32，得到D（-52，0），由题意知F（-8+2t，0），根据S△ABF=2S△ABF求出t．
（1）
解：∵（a＋1）2＋b−2＝0，
∴a+1=0，b-2=0，
解得a=-1，b=2；
（2）
如图，过P作直线l⊥x轴，延长AB交直线l于点Q，
设Q的坐标为（3，m），

过A作AH⊥l交直线l于点H，
∵S△AHQ=S△ABH+S△BQH
∴12×3+1×m−1=12×3+1×3−1+12×3−2×m−1
解得m=113，
∴Q（3，113），
∵S△ABP=S△AQP−S△BPQ=12×PQ×3+1−12×PQ×3−2=32PQ，
又∵点P（3，n）满足△ABP的面积等于6，
∴32n−113=6
解得n=233或−13；
（3）
如图，延长BA交x轴于D，过A作AG⊥x轴于G，过B作BN⊥x轴于N，

∵S梯形AGOC+S梯形CONB=S梯形AGNB,
∴121+OC×1+12×2×OC+3=12×1+3×3
解得OC=53，
∵S△ADG+S梯形AGNB=S△DNB，
∴12DG×1+12×1+3×3=12×3×DG+3，
解得DG=32，
∵G（-1，0），
∴D（-52，0），
由题意知，当t秒时，F（-8+2t，0），
∴DF=−8+2t−−52=2t−112，
∵CE=t，
∴S△ABE=12CE×2−−1=32t，S△ABF=S△BDF−S△DAF=12DF×3−1=2t−112，
∵S△ABF=2S△ABF，
∴22t−112=32t，
解得t=225或2．
【点睛】此题考查了偶次方的非负性及算术平方根的非负性，一元一次方程的实际应用，动点问题，正确掌握一元一次方程与几何图形的知识是解题的关键．