山东省德州市临邑县2021-2022学年七年级下学期期末考试数学试卷

这是一份山东省德州市临邑县2021-2022学年七年级下学期期末考试数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年山东省德州市临邑县七年级（下）期末数学试卷一、选择题（本大题共12小题，共48分。在每小题列出的选项中，选出符合题目的一项）如图所示各图中，与是对顶角的是(    )A.  B.
C.  D. 以下点在第二象限的是(    )A.  B.  C.  D. 下列实数中，是无理数的是(    )A.  B.  C.  D. 如图，可以得到的条件是(    )A.
B.
C.
D. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏，如图，是一局象棋残局，若表示棋子“炮”和“車”的点的坐标分别为，，则表示棋子“馬”的点的坐标为(    )
A.  B.  C.  D. 一个两位数，十位数字比个位数字大；将这个两位数的十位数字与个位数字对调后，比原数减少了，求原两位数．若设原两位数十位数字是，个位数字是，则列出方程组为(    )A.  B.
C.  D. 若关于，的方程是二元一次方程，则的值为(    )A.  B.  C.  D. 是不等式的一个解，则的值不可能是(    )A.  B.  C.  D. 已知关于的二元一次方程组，给出下列说法：若与互为相反数，则：若，则的最大整数值为；若，则其中正确的有(    )A. 个 B. 个 C. 个 D. 个已知一组数据：，，，，，其中无理数出现的个数是(    )A. 个 B. 个 C. 个 D. 个下列说法正确的是(    )A. 为了解人造卫星的设备零件的质量情况，应选择抽样调查
B. 调查某批次汽车的抗撞击能力适合用全面调查
C. 了解北京冬奥会的收视率适合用抽样调查
D. 从全校名学生中抽取名调查了解寒假阅读情况，抽取的样本容量为小杨在商店购买了件甲种商品，件乙种商品，共用元，已知甲种商品每件元，乙种商品每件元，那么的最大值是
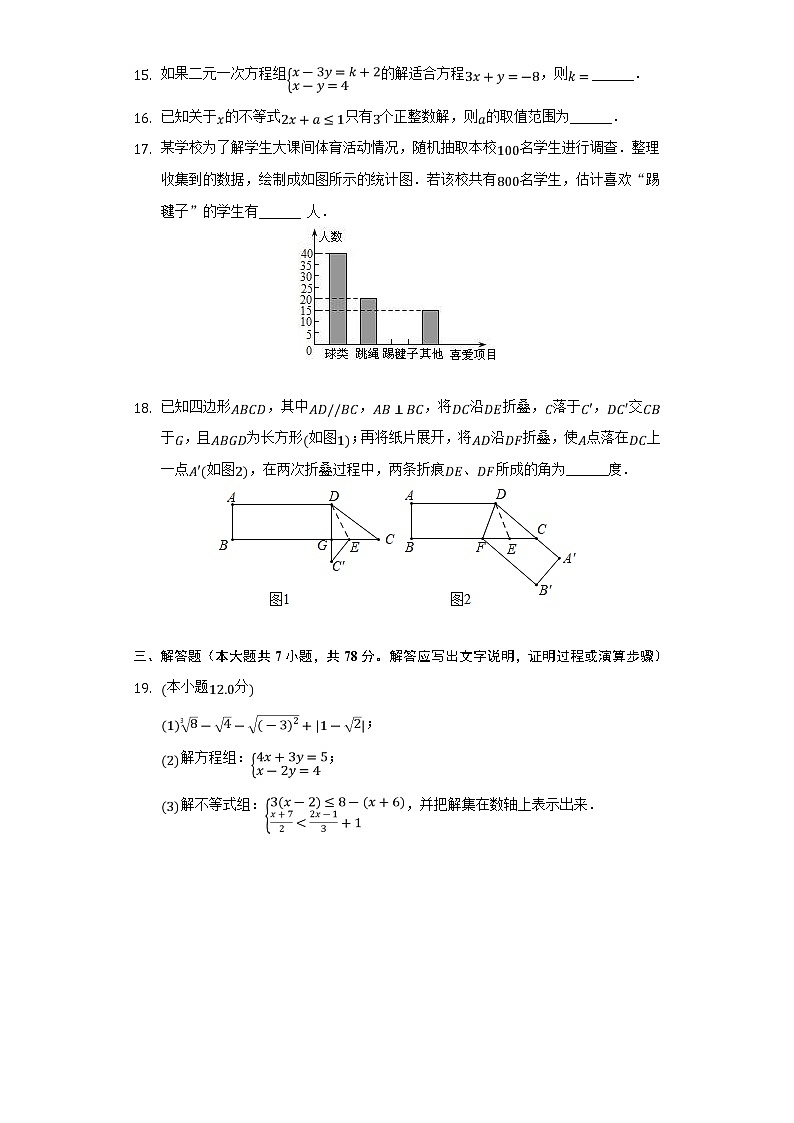
(    )A.  B.  C.  D.  二、填空题（本大题共6小题，共24分）若一个数的平方等于，则这个数等于______．在平面直角坐标系中，把点向右平移个单位长度，平移后对应点坐标为______．如果二元一次方程组的解适合方程，则______．已知关于的不等式只有个正整数解，则的取值范围为______．某学校为了解学生大课间体育活动情况，随机抽取本校名学生进行调查．整理收集到的数据，绘制成如图所示的统计图．若该校共有名学生，估计喜欢“踢毽子”的学生有______ 人．
已知四边形，其中，，将沿折叠，落于，交于，且为长方形如图；再将纸片展开，将沿折叠，使点落在上一点如图，在两次折叠过程中，两条折痕、所成的角为______度．
三、解答题（本大题共7小题，共78分。解答应写出文字说明，证明过程或演算步骤）本小题分
；
解方程组：；
解不等式组：，并把解集在数轴上表示出来．        本小题分
随着社会的发展，私家车变得越来越普及，为节省能源提倡使用节能低油耗汽车，被抽样的某型号汽车，在耗油的情况下所行驶的路程单位：，结果如图所示．
注：记为，为，为，为，为
请依据统计结果回答以下问题：
试求进行该试验的车辆数；
请补全频数分布直方图；
求扇形的圆心角的度数．
 
本小题分
青山化工厂与、两地有公路、铁路相连，这家工厂从地购买一批每吨元的原料经铁路和公路运回工厂，制成每吨元的产品经铁路和公路销售到地．已知铁路的运价为元吨千米，公路的运价为元
吨千米，且这两次运输共支出铁路运费元，公路运费元．
设原料重吨，产品重吨，根据题中数量关系填写表： 原料吨产品吨合计元铁路运费______ ______ 公路运费______ ______ 这批产品的销售款比原料费与运输费的和多多少元？ 本小题分
如图，直线、相交于点，，射线把分成两个角，且：：．
求的度数．
过点作射线，求的度数．
本小题分
如图，三角形是三角形经过某种变换后得到的图形．分别观察点与点，点与点，点与点的坐标之间的关系．
若三角形内任意一点的坐标为点经过这种变换后得到点根据你的发现，点的坐标为______．
若三角形先向上平移个单位，再向右平移个单位得到三角形，画出三角形并求三角形的面积．
本小题分
阅读与思考
请阅读下面材料，并完成相应的任务．
在学习完实数的相关运算之后，某数学兴趣小组提出了一个有趣的问题：两个数的积的算术平方根与这两个数的算术平方根的积存在什么关系？小聪和小明分别用自己的方法进行了验证：
小聪：，所以．
小明：．
这就说明和都是的算术平方根，而的算术平方根只有一个，所以．
任务：
猜想：当，时，和之间存在怎样的关系？并仿照小聪或小明的方法举出一个例子进行说明：
运用以上结论．计算：；；
解决实际问题：已知一个长方形的长为，宽为，求这个长方形的面积．本小题分
已知．，直线与直线、分别交于点、．
如图，若，求的度数；
如图，与的角平分线交于点，与交于点是上一点，求证：．
如图，在的条件下，连接，是上一点使，作平分，向的大小是否发生变化？若不变，请求出其值；若变化，说明理由．
 

答案 1.【答案】 2.【答案】 3.【答案】 4.【答案】 5.【答案】 6.【答案】 7.【答案】 8.【答案】 9.【答案】 10.【答案】 11.【答案】 12.【答案】 13.【答案】 14.【答案】 15.【答案】 16.【答案】 17.【答案】 18.【答案】 19.【答案】解：

；
，
得：
，
得：
，
解得：，
把代入得：
，
解得：，
原方程组的解为：；
，
解不等式得：，
解不等式得：，
原不等式组无解，
该不等式组的解集在数轴上表示如图所示：
 20.【答案】解：辆，
答：进行该试验的车辆数为辆；
“”的车辆数为辆，
“”的车辆数为辆，
补全频数分布直方图如下：

，
答：扇形的圆心角的度数为． 21.【答案】解：由题意可得：；；
；；
故答案为：；；；；

由题意可得：，
解得：，
故元，
答：这批产品的销售款比原料费与运输费的和多元．
直接利用公路与铁路的购进与销售的路程乘以铁路的运价为元吨千米，公路的运价为元吨千米，进而得出答案；
利用这两次运输共支出铁路运费元，公路运费元，得出等式组成方程组求出答案．
22.【答案】解：设，则，
，
，
，
，
，
；
如图，
，
，
，
；
如图，
，
，
又已求，
．
的度数是或． 23.【答案】解：根据观察图象可知，与是关于原点成中心对称，
则点与点关于原点对称，
故点的坐标为，
故答案为：；

如图，即为所求．

，
故的面积为．
 24.【答案】解：当，时，；
例如：，，
；
：


；



；
长方形的长为，宽为，
，
答：这个长方形的面积为． 25.【答案】解：，
，
，
；
证明：由知，，
．
又与的角平分线交于点，
，
，
即，
，
；
解：的大小不发生变化，度数为，理由如下：
，，
．
又，
，
，
平分，
，
，
故的大小不发生变化，度数为．