九年级数学下册北京市清华大学附属中学开学考试附答案解析

清华附中朝阳学校朝阳学校初三数学开学检测

一、选择题（本题共24分，每小题3分）

1. 下列图形中，既是中心对称图形也是轴对称图形的是（    ）

A.  B.  C.  D.

2. 抛物线的顶点坐标是（　　）

A.  B.  C.  D.

3. 在中，，，，则的长为（   ）

A. 2 B. 3 C.  D.

4. 点，点，在反比例函数的图象上，且，则（   ）

A.  B.  C.  D. 不能确定

5. 如图，，是⊙的半径，若，则的度数是（   ）

A.  B.  C.  D.

6. 若正多边形的一个外角是，则该正多边形的边数是（    ）

A. 3 B. 4 C. 5 D. 6

7. 在中，，， ，则的长为（   ）

A.  B.  C. 或 D. 或

8. 已知抛物线上部分点的横坐标x与纵坐标y的对应值如下表：

有以下几个结论：

①抛物线的开口向上；

②抛物线的对称轴为直线；

③关于x的方程的根为和；

④当y＜0时，x取值范围是＜x＜．

其中正确的是（   ）

A. ①④ B. ②④ C. ②③ D. ③④

二、填空题（本题共24分，每小题3分）

9. 如图：在中，，，，则________．

10. 如果一个二次函数图象开口向下，对称轴为，则该二次函数表达式可以为______．（任意写出一个符合条件的即可）

11. 在中，，，，那么__________．

12. 如图，圆心角为120°，半径为4的弧，则这条弧的长度为是______．

13. 如图所示的网格是正方形网格，则______°（点，，，是网格线交点）

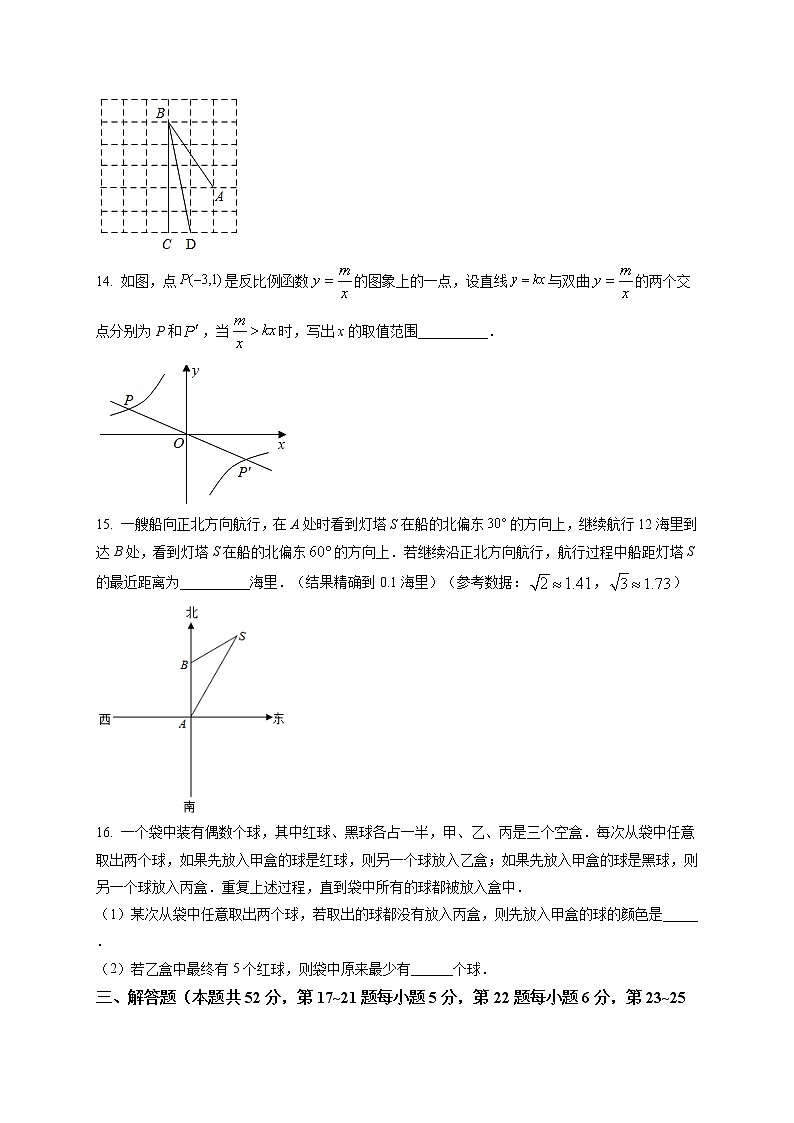
14. 如图，点是反比例函数的图象上的一点，设直线与双曲的两个交点分别为P和，当时，写出x的取值范围__________．

15. 一艘船向正北方向航行，在A处时看到灯塔S在船的北偏东的方向上，继续航行12海里到达B处，看到灯塔S在船的北偏东的方向上．若继续沿正北方向航行，航行过程中船距灯塔S的最近距离为__________海里．（结果精确到0.1海里）（参考数据：，）

16. 一个袋中装有偶数个球，其中红球、黑球各占一半，甲、乙、丙是三个空盒．每次从袋中任意取出两个球，如果先放入甲盒的球是红球，则另一个球放入乙盒；如果先放入甲盒的球是黑球，则另一个球放入丙盒．重复上述过程，直到袋中所有的球都被放入盒中．

（1）某次从袋中任意取出两个球，若取出的球都没有放入丙盒，则先放入甲盒的球的颜色是_____．

（2）若乙盒中最终有5个红球，则袋中原来最少有______个球．

三、解答题（本题共52分，第17~21题每小题5分，第22题每小题6分，第23~25题每小题7分）解答应写出文字说明、证明过程或演算步骤.

17. 计算：．

18. 下面是小付设计的“过圆上一点作圆的切线”的尺规作图过程．

已知：如图，⊙O及⊙O上一点P．

求作：过点P的⊙O的切线．

作法：如图，

①作射线OP；

②以点P圆心，PO为半径作⊙P，与射线OP交于另一点B；

③分别以点O，点B为圆心，大于PO长为半径作弧，两弧交射线OP上方于点D；

④作直线PD；

则直线PD即为所求．

根据小付设计的尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明：

证明：∵ ，，

∴ （____________）（填推理的依据）．

又∵ OP是⊙O的半径，

∴ PD是⊙O的切线（____________）（填推理的依据）．

19. 关于的一元二次方程．

（1）求证：方程总有两个实数根；

（2）若方程有一个根为负数，求的取值范围．

20. 如图，在平面直角坐标系xOy中，△AOB的顶点坐标分别是A(1，0)，O(0，0)，B(2，2)．

（1）画出A1OB1，使A1OB1与AOB关于点O中心对称；

（2）以点O为位似中心，将AOB放大为原来的2倍，得到A2OB2，画出一个满足条件的A2OB2．

21. 一个不透明布袋中有完全相同的三个小球，把它们分别标号为1，2，3. 小林和小华做一个游戏，按照以下方式抽取小球：先从布袋中随机抽取一个小球，记下标号后放回布袋中搅匀，再从布袋中随机抽取一个小球， 记下标号. 若两次抽取的小球标号之和为奇数，小林赢；若标号之和为偶数，则小华赢.

（1）用画树状图或列表方法，列出前后两次取出小球上所标数字的所有可能情况；

（2）请判断这个游戏是否公平，并说明理由.

22. 如图，AB是⊙O的直径，C，D是⊙O上两点，且，连接OC，BD，OD．

（1）求证：OC垂直平分BD；

（2）过点C作⊙O的切线交AB的延长线于点E，连接AD，CD．

①依题意补全图形；

②若AD=6，，求CD的长．

23. 已知：抛物线经过点和．

（1）求抛物线的表达式；

（2）设点关于对称轴的对称点为，抛物线与线段恰有一个公共点，结合函数图象，求的取值范围．

24. 在正方形ABCD中，E是CD边上一点（CE>DE），AE，BD交于点F．

（1）如图1，过点F作GH⊥AE，分别交边AD，BC于点G，H．

求证：∠EAB=∠GHC；

（2）AE的垂直平分线分别与AD，AE，BD交于点P，M，N，连接CN．

①依题意补全图形；

图1                  备用图

②用等式表示线段AE与CN之间的数量关系，并证明．

25. 对于平面直角坐标系中的图形M，N，给出如下定义：如果点P为图形M上任意一点，点Q为图形N上任意一点，那么称线段PQ长度的最小值为图形M，N的“近距离”，记作 d（M，N）．若图形M，N的“近距离”小于或等于1，则称图形M，N互为“可及图形”．

（1）当⊙O半径为2时，

①如果点A（0，1），B（3，4），那么d（A，⊙O）=_______,d（B，⊙O）= ________；

②如果直线与⊙O互为“可及图形”，求b的取值范围；

（2）⊙G的圆心G在轴上，半径为1，直线与x轴交于点C，与y轴交于点D，如果⊙G和∠CDO互为“可及图形”，直接写出圆心G的横坐标m的取值范围．

参考答案

1-5   BCCBA   6-8  DDC

9.9   10.   11.    12.       13.45      14.-3＜x＜0或x＞3

15.10.4       16.20

17.4

18.【详解】（1）由题意可得：

作出⊙，标记点；

作出点；

作出直线；

∴DP即为所求直线；

（2）证明：∵ ，，

∴ （垂直平分线的判定），

又∵ OP是⊙O的半径，

∴ PD是⊙O切线（经过半径的外端并且垂直与这条半径的直线是圆的切线）；

故答案为垂直平分线的判定；经过半径的外端并且垂直与这条半径的直线是圆的切线．

19.【详解】（1）证明：依题意，得

．

，

方程总有两个实数根．

（2）解：由求根公式，得．

，．

方程有一个根为负数，

．

．

的取值范围是．

20.【详解】解：（1）如图：A1OB1即为所求作的图形．

（2）如图：A2OB2即为所求作的图形．

21.【详解】解：方法一：（1）由题意画出树状图

所有可能情况如下：

；

（2）由（1）可得：标号之和分别为2，3，4，3，4，5，4，5，6，

，

，

因为，所以不公平；

方法二：（1）由题意列表

所有可能情况如下：

；

（2）由（1）可得：标号之和分别为2，3，4，3，4，5，4，5，6，

，

，

因为，所以不公平．

22.【详解】（1）证明：∵

∴∠COD =∠COB．

∵OD = OB，

∴OC垂直平分BD．

（2）解：①补全图形，如图所示．

②∵CE⊙O切线，切点为C，

∴OC⊥CE于点C．

记OC与BD交于点F，由（1）可知OC垂直BD，

∴∠OCE=∠OFB=90°．

∴DB∥CE．

∴∠AEC=∠ABD．

在Rt△ABD中，AD=6，，

∴BD=8，AB=10．

∴OA= OB=OC=5．

由（1）可知OC平分BD，即DF= BF，

∴BF=DF=4．

∴．

∴CF=2．

在Rt△CFD中，．

23.【详解】解：（1）把和分别代入，

得：，解得：，

抛物线的表达式为：；

（2），对称轴直线，

点关于对称轴的对称点点坐标为，

如图，当过、点时为临界点，

代入，则，

代入，则，

．

24.【详解】（1）证明：在正方形ABCD中，AD∥BC，∠BAD=90°，

∴∠AGH=∠GHC．

∵GH⊥AE，

∴∠EAB=∠AGH．

∴∠EAB=∠GHC．

（2）①补全图形，如图所示．

②．

证明：连接AN，连接EN并延长，交AB边于点Q．

∵四边形ABCD是正方形，

∴点A，点C关于BD对称．

∴NA=NC，∠1=∠2．

∵PN垂直平分AE，

∴NA=NE．

∴NC=NE．

∴∠3=∠4．

在正方形ABCD中，BA∥CE，∠BCD=90°，

∴∠AQE=∠4．

∴∠1+∠AQE=∠2+∠3=90°．

∴∠ANE=∠ANQ=90°．

在Rt△ANE中，

∴．

25.【详解】（1）① 如图：

根据近距离的定义可知：d（A，⊙O）=AC=2-1=1.

过点B作BE⊥x轴于点E，则

OB= =5

∴d（B，⊙O）=OB-OD=5-2=3.

故答案为1，3.

② ∵由题意可知直线与⊙O互为“可及图形”，⊙O的半径为2，

∴．

∴．

  ∴ ．

（2）①当⊙G与边OD是可及图形时，d（O，⊙G）=OG-1,

∴

即-1≤m-1≤1

解得：.