

九年级数学下册北师版·山东省青岛市市北区中考模拟附答案解析
展开2021年山东省青岛市市北区中考数学模拟试卷
一、选择题(本大题共8小题,共24分)
1. 与的关系是( )
A. 相等 B. 互为相反数
C. 前式是后式的倍 D. 以上结论都不对
2. 下列图形是轴对称图形的是( )
A. B. C. D.
3. 据统计,我省2019年生产总值约为37100亿元,其中“37100亿”用科学记数法表示为( )
A. 3.71×1012 B. 3.71×1011 C. 0.371×105 D. 3.71×104
4. 下列运算正确的是( )
A. B. C. D.
5. 以原点为中心,把点逆时针旋转,得点,则点坐标是( )
A. B. C. D.
6. 如图,内接于⊙,,则度数为()
A. 110° B. 115° C. 120° D. 125°
7. 若二次函数的顶点在第一象限,且经过点,, 则的变化范围是 ( )
A ; B. ; C. ; D.
8. 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕 DE分别交AB、AC于点E、G,连结GF,给出下列结论:①;② ;③;④四边形 AEFG是菱形;⑤;⑥若,则正方形 ABCD的面积是,其中正确的结论个数为( )
A. 2 B. 3 C. 4 D. 5
二、填空题(本大题共6小题,共18分)
9. ______.
10. 若点(4,m)在反比例函数(x≠0)的图象上,则m的值是_____.
11. 为了解我市城区居民日常出行方式的情况.某学习小组进行了问卷调查,共收回600份调查问卷,结果统计如下:
出行方式 | 坐公交车 | 骑自行车、电动车 | 开私家车 | 坐单位班车 |
人数 | 280 | 240 | 65 | 15 |
根据以上调查结果,在制作扇形统计图时,以“骑自行车、电动车”为出行方式所在扇形的圆心角的度数为______ .
12. 两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米.第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为千米/小时,根据题意可列方程________.
13. 正方形ABCD的边长为4,M为BC的中点,点N在CD边上,且,则 ___.
14. 如图所示为一机器零件的三视图.若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积为_____.
三、解答题(本大题共10小题,共78分)
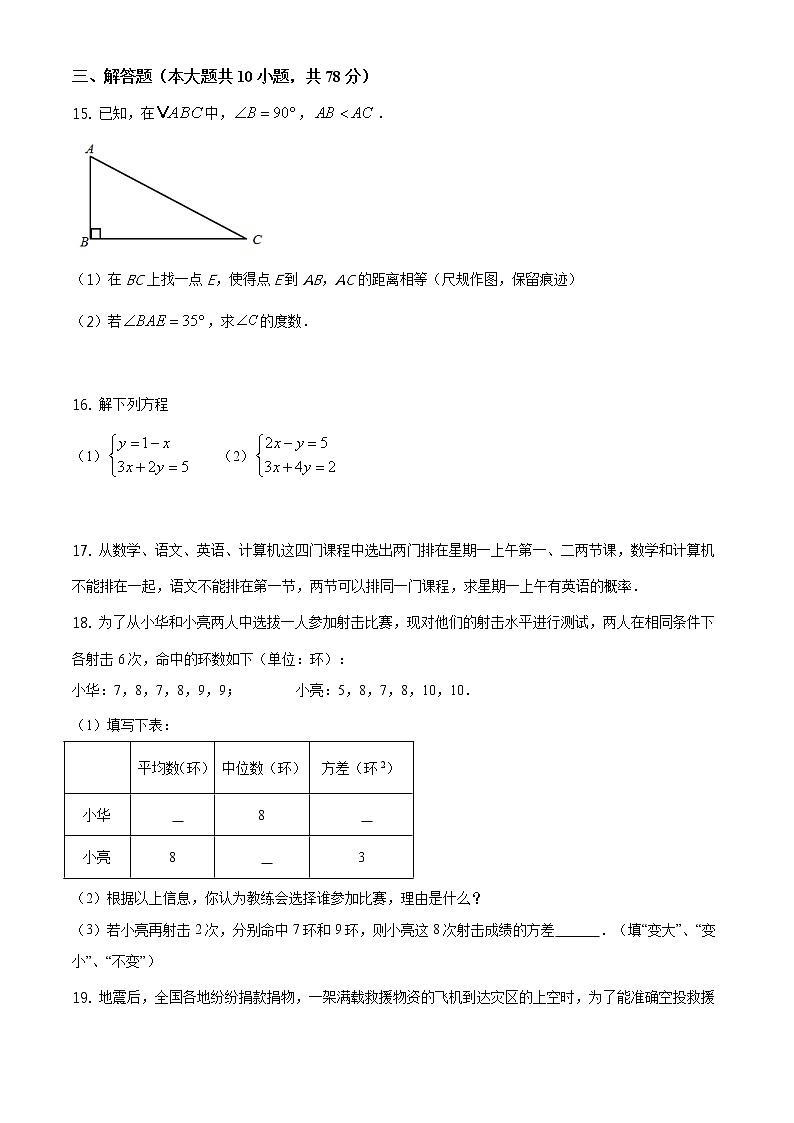
15. 已知,在中,,.
(1)在BC上找一点E,使得点E到AB,AC的距离相等(尺规作图,保留痕迹)
(2)若,求的度数.
16. 解下列方程
(1) (2)
17. 从数学、语文、英语、计算机这四门课程中选出两门排在星期一上午第一、二两节课,数学和计算机不能排在一起,语文不能排在第一节,两节可以排同一门课程,求星期一上午有英语的概率.
18. 为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9; 小亮:5,8,7,8,10,10.
(1)填写下表:
| 平均数(环) | 中位数(环) | 方差(环2) |
小华 |
| 8 |
|
小亮 | 8 |
| 3 |
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,则小亮这8次射击成绩的方差 .(填“变大”、“变小”、“不变”)
19. 地震后,全国各地纷纷捐款捐物,一架满载救援物资的飞机到达灾区的上空时,为了能准确空投救援物资,在A处测得空投动点C的俯角α=60°,测得地面指挥台的俯角β=30°,如果B、C两地间的距离是2000米,则此时飞机距地面的高度是多少米?(结果保留根号)
20. 如图,正比例函数y1=kx与-次函数y2=mx+n的图象交于点A(3,4),一次函数y2的图象与x轴,y轴分别交于点B,点C,且0A=OC.
(1)求这两个函数的解析式;
(2)求直线AB与两坐标轴所围成三角形的面积.
21. 如图,在平面直角坐标系xOy中,已知、,点M、N分别是线段OB、AB上的动点,速度分别是每秒个单位、2个单位,作于现点M、N分别从点O、A同时出发,当其中一点到达端点时,另一个点也随之停止运动,设运动时间为t秒().
(1)是否存在t的值,使四边形BMHN为平行四边形?若存在,求出t的值;若不存在,说明理由;
(2)是否存在t的值,使△OMH与以点A、N、H为顶点的三角形相似?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形BMHN为菱形?若存在,求出t的值;若不存在,请探究将点N的速度改变为何值时(匀速运动),能使四边形BMHN在某一时刻为菱形.
22. 为节约用水、保护水资源,本市制定了一套节约用水管理措施,其中规定每月用水量超过吨时,超过部分每吨加收环境保护费元.下图反映了每月收取的水费元与每月用水量吨之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
月份 | 用水量(吨) | 水费(元) |
四月 | 35 | |
五月 | 80 | 151 |
(1)求出m的值;
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
23. 如图1个正五边形,分别连接这个正五边形各边中点得到图2,再分别连接图2小正五边形各边中点得到图3.
(1)填写如表
图形标号 | 1 | 2 | 3 |
正五边形个数 | ______ | ______ | ______ |
三角形个数 | ______ | ______ | ______ |
(2)按上面方法继续连下去,第n个图中有多少个三角形?
(3)能否分出2014个三角形?简述你的理由.
24. 在四边形ABCD中,点E是线段AC上一点,BE∥CD,∠BEC=∠BAD.
(1)如图1已知AB=AD;
①找出图中与∠DAC相等的角,并给出证明;
②求证:AE=CD;
(2)如图2,若BC∥ED,,∠BEC=45°,求tan∠ABE的值.
参考答案
1-5. BAAAB 6-8. BAB
9. 2 10. 2 11. . 12.
13. 5 14. 24+8
15. 解:(1)如图,点为所作;
(2)点到,的距离相等,
点在的平分线上,即平分,
,
,
.
16. 【详解】(1) ,
把①代入②得:3x+2-2x=5,
解得:x=3,
把x=3代入①得:y=-2,
则方程组的解为.
(2) ,
①×4得:8x-4 y=20③,
③+②得:11x=22,
x=2,
把x=2代入①得:y=-1,
则方程组的解为:.
17. 解:设数学、语文、英语、计算机分别为A、B、C、D,列表得:
∴一共有10种情况,星期一上午有英语的有6种情况,
∴星期一上午有英语的概率为.
18. 【详解】(1)解:小华射击命中的平均数:=8,
小华射击命中的方差:,
小亮射击命中的中位数:;
(2)解:∵小华=小亮,S2小华<S2小亮
∴选小华参赛更好,因为两人的平均成绩相同,但小华的方差较小,说明小华的成绩更稳定,所以选择小华参赛.
(3)解:小亮再射击2次,分别命中7环和9环,则小亮这8次射击成绩的方差变小.
19. 【详解】作AH⊥BC交BC延长线于H,
由题意得,∠ACH=60°,∠ABC=30°,
∴∠BAC=30°,
∴∠ABC=∠BAC,
∴AC=BC=2000米,
∴AH=AC•sin∠ACH=1000米,
答:此时飞机距地面的高度是1000米.
20. 【详解】(1)把A(3,4)代人中.得:3k=4
∴
∴
过点A作AE⊥x轴,垂足为E.
∵A(3,4)
∴OE=3,AE=4
在Rt△OAE中,
又∵OC=OA=5
∴.C(0,-5)
把A(3,4),C(0,-5)代人中,得
∴
∴
(2)在中,令得
∴OB=
∴.
21. 解:∵A(9,0)、B(9,12)
∴OA=9,AB=12,由勾股定理得OB=15
由题意得,BA⊥OA,又MH⊥OA
∴MH∥BA
∴
又∵OM=
∴OH=,MH=
(1)使四边形BMHN为平行四边形,MH=BN即可
即
解得,=3.6
(2)当△OMH∽△HNA时,
即
解得=3.6
当△OMH∽△NHA时,
即
解得=
(3)若四边形BMHN是菱形,则HM=MB=BN
设点N的速度改变为
得
解得=5,=
当点N的速度改变为时,5秒四边形BMHN为菱形.
22. 【详解】(1)由函数图象可知,不超过m吨时,水费为:元/吨,
根据五月份用水量得:,
整理得:,
解得:,,
∵,
∴,
∴;
(2)由(1)可得,当时,,
当时,,
∴关系式为:.
23. 【详解】(1)观察图形可得:
图1,正五边形:1个,三角形:0个;
图2,正五边形:2个,三角形:5个;
图3,正五边形:3个,三角形:10个;
故答案为:第一行:1,2,3;第二行:0,5,10;
(2)由前三个图形中三角形的个数得出:
第n个图形中,三角形的个数为:个;
(3)不能,理由如下:
要使得分出2014个三角形,
即满足,其中n为正整数即可,
而上式解得,,并非正整数,
∴不能分出2014个三角形.
24. 解:(1)①∠ABE=∠CAD,
理由如下:以D为圆心,DC为半径画圆,交AC于F,连接DF,
则CD=DF,
∴∠DFC=∠DCF,
∵BE∥CD,
∴∠BEC=∠FCD,
∴∠BEC=∠DFC,
∴∠AEB=∠AFD,
∠BEC=∠BAE+∠ABE,∠BAD=∠BAE+∠DAF,∠BEC=∠BAD,
∴∠ABE=∠DAF,
在△ABE和△DAF中,
,
∴△ABE≌△DAF(AAS),
∴∠ABE=∠CAD,
②∵△ABE≌△DAF,
∴AE=DF,
∵CD=DF,
∴AE=CD;
(3)过点D作DG⊥CD交AC于点G,
∵BE∥CD,
∴∠DCA=∠BEC=45°,
∴∠AEB=∠DGA=135°,DG=DC,
∵∠AEB=∠DGA,∠ABE=∠DAG,
∴△ABE∽△DAG,
∴==,
∵BC∥DE,BE∥CD,
∴四边形BCDE为平行四边形,
∴BE=CD,
过点A作AH垂直于BE交BE的延长线于点H,
设AH=EH=m,
则AE=m,DG=CD=BE=2m,
∴BH=BE+EH=2m+m,
tan∠ABE===.
2021北师版·山东省青岛市市北区中考模拟九年级下册数学试题: 这是一份2021北师版·山东省青岛市市北区中考模拟九年级下册数学试题,共12页。试卷主要包含了选择题,填空题,解答题,五两月用水量及缴费情况如表等内容,欢迎下载使用。
2023年山东省青岛市市北区中考数学三模试卷(含解析): 这是一份2023年山东省青岛市市北区中考数学三模试卷(含解析),共28页。试卷主要包含了选择题.,填空题,解答题等内容,欢迎下载使用。
2023年山东省青岛市市北区中考数学三模试卷(含解析): 这是一份2023年山东省青岛市市北区中考数学三模试卷(含解析),共29页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












