2023年云南省昆明八中中考数学模拟试卷（一）（含解析）

这是一份2023年云南省昆明八中中考数学模拟试卷（一）（含解析），共19页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
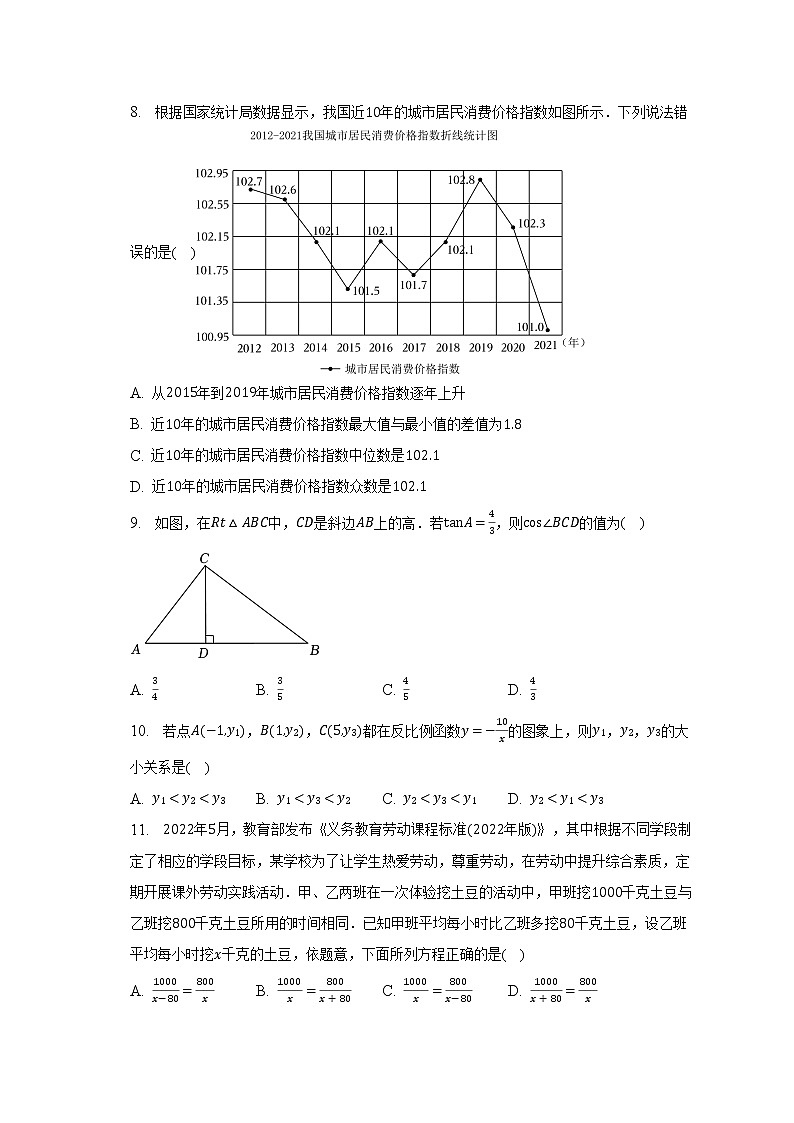
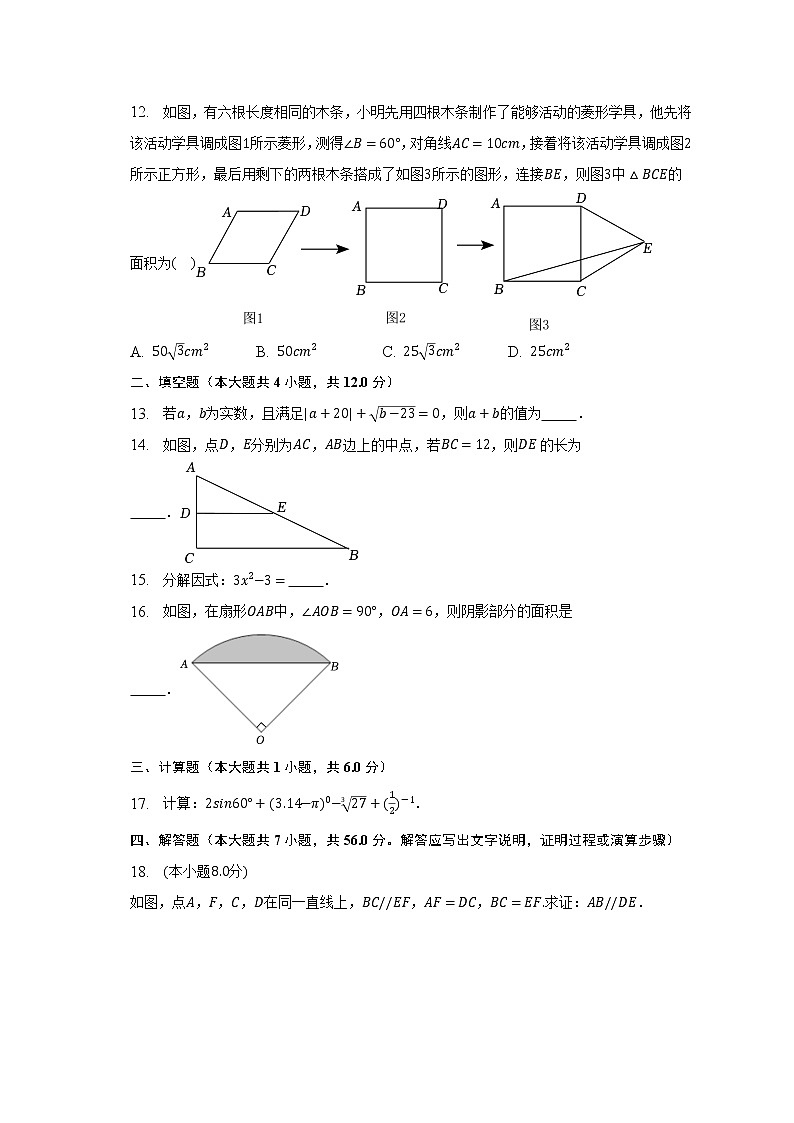
2023年云南省昆明八中中考数学模拟试卷（一）一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）1.  中国是最早采用正负数表示相反意义，并进行负数运算的国家．若把气温为零上记作，则表示气温为(    )A. 零上 B. 零下 C. 零上 D. 零下2.  疫情管控放开，旅游行业触底反弹，文旅消费需求剧增．据云南省文化和旅游厅消息，年春节假日期间，云南省共接待游客万人次，实现旅游收入亿元．其中数据用科学记数法可表示为(    )A.  B.  C.  D. 3.  如图，把一块三角板的直角顶点放在直线上，，，则 的度数为(    )A.  B.  C.  D. 4.  在如图所示的几何体中，主视图和俯视图相同的是(    )A.  B.  C.  D. 5.  下列计算正确的是(    )A.  B.  C.  D. 6.  一个多边形的内角和是其外角和的倍，则这个多边形是(    )A. 六边形 B. 七边形 C. 八边形 D. 九边形7.  观察下列按一定规律排列的数：，，，，，，，，，则第个数为(    )A.  B.  C.  D. 8.  根据国家统计局数据显示，我国近年的城市居民消费价格指数如图所示．下列说法错误的是(    )A. 从年到年城市居民消费价格指数逐年上升
B. 近年的城市居民消费价格指数最大值与最小值的差值为
C. 近年的城市居民消费价格指数中位数是
D. 近年的城市居民消费价格指数众数是9.  如图，在中，是斜边上的高．若，则的值为(    )A.  B.  C.  D. 10.  若点，，都在反比例函数的图象上，则，，的大小关系是(    )A.  B.  C.  D. 11.  年月，教育部发布义务教育劳动课程标准年版，其中根据不同学段制定了相应的学段目标，某学校为了让学生热爱劳动，尊重劳动，在劳动中提升综合素质，定期开展课外劳动实践活动．甲、乙两班在一次体验挖土豆的活动中，甲班挖千克土豆与乙班挖千克土豆所用的时间相同．已知甲班平均每小时比乙班多挖千克土豆，设乙班平均每小时挖千克的土豆，依题意，下面所列方程正确的是(    )A.  B.  C.  D. 12.  如图，有六根长度相同的木条，小明先用四根木条制作了能够活动的菱形学具，他先将该活动学具调成图所示菱形，测得，对角线，接着将该活动学具调成图所示正方形，最后用剩下的两根木条搭成了如图所示的图形，连接，则图中的面积为(    )A.  B.  C.  D. 二、填空题（本大题共4小题，共12.0分）13.  若，为实数，且满足，则的值为          ．14.  如图，点，分别为，边上的中点，若，则 的长为          ．15.  分解因式：          ．16.  如图，在扇形中，，，则阴影部分的面积是          ．三、计算题（本大题共1小题，共6.0分）17.  计算：．四、解答题（本大题共7小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）18.  本小题分如图，点，，，在同一直线上，，，求证：．19.  本小题分奋进新征程，云南怎么干．云南省政府工作报告建言献策收获满满，网友针对年云南怎么干和未来年云南怎么干，纷纷畅所欲言，展望云南未来发展之路，共收到条来自全国各地网友的有效建言，其中条建言在政府工作报告中有所体现，为云南省年政府工作报告的起草贡献了基层智慧，年的政府工作报告干货满满，鼓舞人心，催人奋进，让人充满期待．某中学为了引导学生关注家乡，建设云南，针对全校学生举行“奋进新征程，云南怎么干”的主题知识竞赛．从中随机抽查了部分参赛学生的成绩，并绘制了如下不完整的成绩频数分布直方图和扇形统计图．抽取竞赛成绩的频数分布直方图和扇形统计图．请根据图表信息解答下列问题：一共抽查了多少名学生？在图中，____，____；抽取竞赛成绩的扇形统计图中，求组所在的扇形圆心角的度数；若该校共有名学生，请估计该校学生参加“奋进新征程，云南怎么干”的主题知识竞赛成绩不低于分的有多少名？20.  本小题分年的春节档电影竞争激烈，多部贺岁片上影，点燃新春，浓浓的年味让人们感受到了久违的热闹景象．小亮和小丽分别从满江红无名流浪地球熊出没伴我“熊心”四部电影中随机选择一部观看，将满江红表示为，无名表示为，流浪地球表示为，熊出没伴我“熊心”表示为小亮从这部电影中，随机选择部观看，则他选中满江红的概率为____；请用列表法或树状图法中的一种方法，求小亮和小丽恰好选择观看同一部电影的概率． 21.  本小题分如图，在四边形中，，过点作的角平分线交于点，连接交于点，．求证：四边形是菱形；若，的周长为，求菱形的面积．22.  本小题分年冬季奥运会和冬季残奥会两项赛事在我国首都北京和河北省石家庄市举行．某商家购进了一批冬季残奥会吉祥物“雪容融”纪念品，发现进价为元件的纪念品每月的销售量件与售价元件的相关信息如下：售价元销售量件求与的一次函数解析式；若获利不得高于进价的，那么售价定为多少元件时，月销售利润达到最大？最大利润是多少元？ 23.  本小题分如图，是的直径，点是上的一动点不与点，点重合，点是延长线上的一点，连接，，，且有，作的平分线交于点，交于点．求证：是的切线；【问题探究】若，，则的值为____；【拓展延伸】若，，求的值．用含和的代数式表示24.  本小题分已知抛物线与轴交于、两点点位于点的左侧，设是抛物线与轴交点的横坐标，抛物线与轴交于点．点是抛物线上的一个动点，若，求所有满足条件的的面积之和；求代数式值．
答案和解析 1.【答案】 【解析】【分析】此题主要用正负数来表示具有意义相反的两种量：若零上记为正，则零下就记为负，直接得出结论即可．【解答】解：若把气温为零上记作，则表示气温为零下故选：．  2.【答案】 【解析】【分析】科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数．【解答】解：．故选：．  3.【答案】 【解析】【分析】根据平行线的性质，可以得到的度数，再根据，可以得到的度数．【解答】解：  ，，．，，故选：．  4.【答案】 【解析】【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形进行分析．【解答】解：主视图和俯视图是正方形，故本选项符合题意；主视图是一行两个相邻的矩形，俯视图是三角形，故本选项不合题意；主视图是矩形，俯视图是圆，故本选项不合题意；主视图是三角形，俯视图是带圆心的圆，故本选项不合题意．故选：．  5.【答案】 【解析】【分析】分别根据同底数幂的除法法则，幂的乘方与积的乘方法则对各选项进行分析即可．【解答】解：、，原计算错误，不符合题意；、，原计算错误，不符合题意；、，原计算错误，不符合题意；、，正确，符合题意．故选：．  6.【答案】 【解析】【分析】根据多边形的内角和定理，多边形的内角和等于，外角和等于，然后列方程求解即可．【解答】解：设多边形的边数是，根据题意得，，解得：，这个多边形为六边形．故选：．  7.【答案】 【解析】【分析】由题意归纳出数字符号与绝对值出现的规律进行求解．【解答】解：由题意得，第个数为，第个数为，，第个数为，故选：．  8.【答案】 【解析】【分析】结合折线统计图，依据极差、中位数和众数的概念求解即可．【解答】解：从年到年城市居民消费价格指数在到年有下降，此选项错误，符合题意；近年的城市居民消费价格指数最大值与最小值的差值为，此选项正确，不符合题意；这组数据为、、、、、、、、、，所以近年的城市居民消费价格指数中位数是，此选项正确，不符合题意；这组数据的众数是，此选项正确，不符合题意．故选：．  9.【答案】 【解析】【分析】根据直角三角形的性质可知，，可得，根据，可得，进一步可得．【解答】解：在中，，，是斜边上的高，，，，，，．设，则，在中，根据勾股定理，可得，，，故选：．  10.【答案】 【解析】【分析】根据，可得反比例函数图象和增减性，即可进行比较．【解答】解：，反比例函数经过第二、四象限，且在每一象限内，随着增大而增大，根据，，点横坐标，可知点，在第四象限，在第二象限，．故选：．  11.【答案】 【解析】【分析】根据甲班挖千克土豆与乙班挖千克土豆所用的时间相同，列分式方程即可．【解答】解：根据题意，得，故选：．  12.【答案】 【解析】【分析】根据菱形的性质可知，过点作，交的延长线于点，根据等边三角形的性质可知，根据含角的直角三角形的性质可得的长，再根据的面积求解即可．【解答】解：图连接．菱形中，，，是等边三角形，对角线，，，图过点作，交的延长线于点，是等边三角形，，，，的面积，故选：．  13.【答案】 【解析】【分析】根据绝对值和算术平方根的非负数的性质列出方程求出、的值，代入所求代数式计算即可．【解答】解：，为实数，且满足，，，，，解得：，，．故答案为：．  14.【答案】 【解析】【分析】根据三角形中位线定理即可得到结论．【解答】解：点，分别为，边上的中点，是的中位线，，，，故答案为：．  15.【答案】 【解析】【分析】首先提取公因式，然后运用平方差公式继续进行因式分解．【解答】解：，，．  16.【答案】 【解析】【分析】根据扇形即可计算．【解答】解：，，是等腰直角三角形．扇形．故答案为：．  17.【答案】解：原式． 【解析】原式第一项利用特殊角的三角函数值计算，第二项利用零指数幂法则计算，第三项化为最简二次根式，最后一项利用负整数指数幂法则计算即可得到结果．
 18.【答案】证明：  ，，，，在和中，，≌，，  ． 【解析】由“”可证≌，可得，可证  ．
 19.【答案】解：名答：一共抽查了名学生．；．答：组所在的扇形圆心角的度数为．名，答：估计该校学生参加“奋进新征程，云南怎么干”的主题知识竞赛成绩不低于分的有名． 【解析】由组人数及其所占百分比即可得出答案；根据四组人数之和等于总人数可得的值，再用的值除以总人数乘可得的值；用乘组对应的百分比即可得出答案；总人数乘、百分比之和即可得出答案．
 20.【答案】解：．画树状图得：共有种等可能的结果，其中小亮和小丽恰好选择观看同一部电影的有种结果，小亮和小丽恰好选择观看同一部电影的概率为． 【解析】直接根据概率公式求解即可；画树状图列出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可．
 21.【答案】证明：  ，  ，四边形是平行四边形，．平分，，，，平行四边形是菱形．解：由可知，四边形是菱形，，，，，的周长为，，．在中，由勾股定理得：，，菱形的面积． 【解析】证四边形是平行四边形，，再证，则，然后由菱形的判定即可得出结论；由菱形的性质得，，，，再求出，则，然后由勾股定理得，则，即可解决问题．
 22.【答案】解：由表格知，售价每增加元，销售量对应减少元，所以这个函数是一次函数．设其解析式为，根据题意，得，解得，与的表达式为．设利润为元，则，，，，当时，，答：售价定为元时，月销售利润最大为元． 【解析】利用待定系数法解答，即可求解；根据利润等于每件的利润乘销售量，列出函数关系式，再根据二次函数的性质，即可求解．
 23.【答案】证明：连接，是的直径，，．，．
．，，，是的半径，是的切线．
 解：【问题探究】，，．，，，，．平分，，，∽，，．故答案为：；【拓展延伸】，，，，，，，．是的直径，，，，平分，，，∽，，
  【解析】连接，根据圆周角定理得到，根据等腰三角形的性质得到，求得，根据切线的判定定理即可得到结论；【问题探究】根据三角形的内角和定理得到，根据等腰三角形的性质得到，求得，根据角平分线的定义得到，根据相似三角形的性质即可得到结论；【拓展延伸】根据三角形的内角和定理得到，根据等腰三角形的性质得到，求得，，根据角平分线的定义得到，根据相似三角形的性质即可得到结论．
 24.【答案】解：设，，，，抛物线与轴交于、两点点位于点的左侧，，，．抛物线与轴交于点，，．设，则，，，解得：．当时，，解得：或．当时，，解得：或，符合题意的点坐标为或或或，共个不同的点．，所有满足条件的的面积之和为．是抛物线与轴交点的横坐标，，则，且，，． 【解析】设，，，，利用根与系数关系得：，，进而可得，由题意得，，设，根据，可得，进而可求得的个值，即满足条件的三角形有个，即可求得答案；根据题意可得：，则，利用代数式的恒等变形可得，代入原式求值即可．