专题04 【大题限时练四】-备战2023年江苏高考数学满分限时题集

这是一份专题04 【大题限时练四】-备战2023年江苏高考数学满分限时题集，文件包含专题04大题限时练四-备战2023年江苏高考数学满分限时题集解析版docx、专题04大题限时练四-备战2023年江苏高考数学满分限时题集原卷版docx等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。
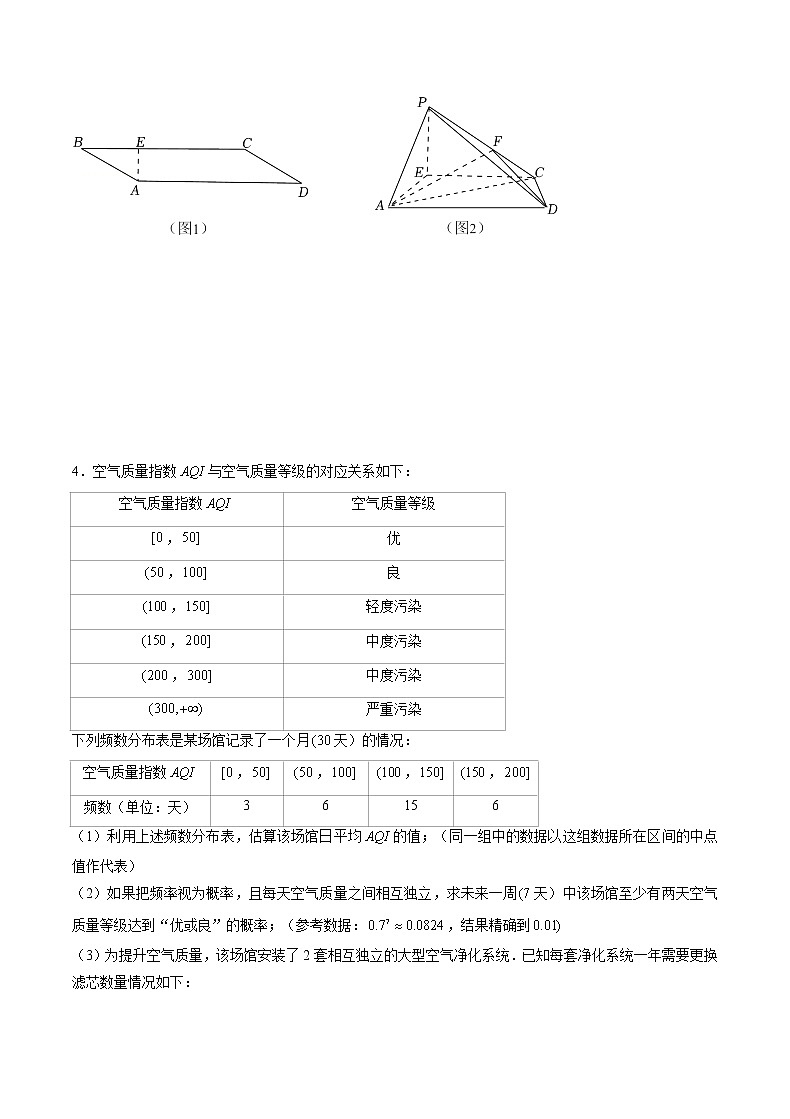
专题04 大题限时练四 1．若数列满足：，，对于任意的，都有．（1）证明：数列是等比数列；（2）求数列的通项公式．【答案】（1）见解析；（2）【解析】（1）证明：由，得，即，又，，得，所以是以2为首项，以3为公比的等比数列；（2）由（1）可知，故，所以，又，所以是以为首项，以为公差的等差数列，，故．2．在平面四边形中，，，，．（1）求的面积；（2）求的长．【答案】（1）；（2）【解析】（1）中，由余弦定理得，，即，所以，的面积；（2）中，由正弦定理得，，所以，同理，中，由正弦定理得，因为，，所以，所以，所以，所以．3．如图1，在平行四边形中，，，，，垂足为．以为折痕把折起，使点到达点的位置，且平面与平面所成的角为（如图．（1）求证：；（2）若点在线段上，且二面角的大小为，求三棱锥的体积． 【答案】（1）见解析；（2）【解析】（1）证明：平面与平面所成的角为，平面平面，平面平面，，平面，平面，平面，．（2）平面，，，，，，两两垂直，以为坐标原点，，，所在直线分别为，，轴，建立如图所示的空间直角坐标系， 在中，，，，，则，，，，，，，，0，，，0，，设，则，，，，，，，，，，设平面的一个法向量为，，，则，设，则，平面的一个法向量为，0，，二面角为，，解得，，到平面的距离为，，三棱锥的体积为．4．空气质量指数与空气质量等级的对应关系如下：空气质量指数空气质量等级，优，良，轻度污染，中度污染，中度污染严重污染下列频数分布表是某场馆记录了一个月天）的情况：空气质量指数，，，，频数（单位：天）36156（1）利用上述频数分布表，估算该场馆日平均的值；（同一组中的数据以这组数据所在区间的中点值作代表）（2）如果把频率视为概率，且每天空气质量之间相互独立，求未来一周天）中该场馆至少有两天空气质量等级达到“优或良”的概率；（参考数据：，结果精确到（3）为提升空气质量，该场馆安装了2套相互独立的大型空气净化系统．已知每套净化系统一年需要更换滤芯数量情况如下：更换滤芯数量（单位：个）345概率0.20.30.5已知厂家每年年初有一次滤芯促销活动，促销期内每个滤芯售价1千元，促销期结束后每个滤芯恢复原价2千元．该场馆每年年初先在促销期购买个滤芯，如果不够用，则根据需要按原价购买补充．问该场馆年初促销期购买多少个滤芯，使当年购买滤芯的总花费最合理，请说明理由．（不考虑往年剩余滤芯和下一年需求）【答案】见解析【解析】（1）法一：；法二：；（2）一个月30天中达到优或良的天数为9，空气质量等级达到优或良的概率为，未来一周天）中该场馆至少有两天空气质量达到优或良的概率为；（3）按照这个数据，每年需要6到10个滤芯，也就是，9，10，而需求假设为，会有，，，那么当时，会有花费的分布为，，，均值，同理算出，，故此买9个最划算．5．已知双曲线，四点，，，中恰有三点在上．（1）求的方程；（2）过点的直线交于，两点，过点作直线的垂线，垂足为．证明：直线过定点．【答案】（1）；（2）见解析【解析】（1）由题意可知点，两点关于原点对称，所以，一定在双曲线上，而，因为，但，所以点不在双曲线上，所以点，，在双曲线上，则，解得，，所以双曲线方程为；（2）证明：设直线的方程为，代入双曲线方程可得：，设，，，，则，则，，所以直线的方程为：，即，令，则，因为，，所以，所以，综上，直线过定点．6．已知函数．（1）讨论的单调性；（2）若，证明：．【答案】见解析【解析】（1）解：函数的定义域为，求导得，当时，恒成立，则在上单调递增，当时，的解集为，的解集为，即的单调递增区间为，单调递减区间为，所以，当时，在上单调递增，当时，在上单调递增，在上单调递减．（2）证明：因为，由（1）知，，且（a），解得，设，则，要证，即证，即证，即证，设．，则，即在上单调递减，有（a），即，，则成立，因此成立，要证，即证，即证，即证，即证，，而，即证，，令，，则，设，，求导得，即在上单调递增，则有（e），即，在上单调递减，而，，，当时，（a）（e），则当时，成立，故有成立，所以．