沪科版数学八年级上第第11章平面直角坐标系11.1平面内点的坐标（第1课时） PPT课件+教学详案

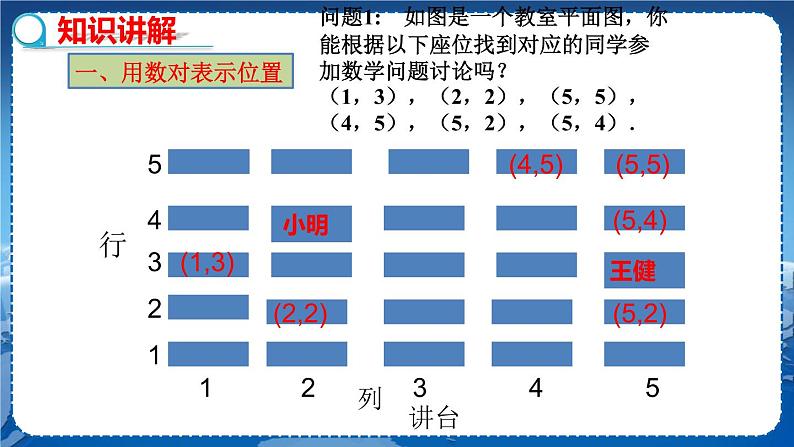
教学目标

1.认识并能画出平面直角坐标系，了解其相关概念.

2.学会用坐标系描述点的位置的方法；由坐标系中指定点的位置写出它的坐标.

3.运用坐标系内点的坐标特点解决一些简单问题.

教学重难点

重点：能根据点的位置说明点的坐标，能根据点的坐标确定点的位置.

难点：深刻理解象限内点的坐标特点及点到坐标轴的距离与点的坐标的关系.

教学过程

复习巩固

1.什么是数轴？

2.什么叫数轴上点的坐标？数轴上的点与实数有什么关系？

探究新知

一、平面直角坐标系

问题：怎样确定教室里小明和王健的位置.

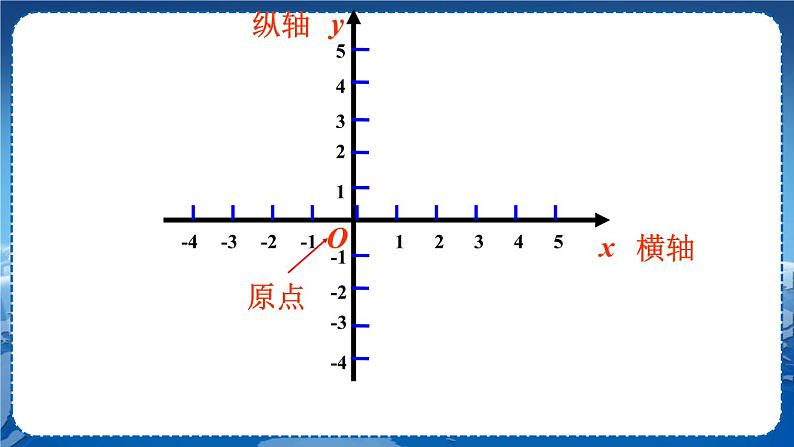
                    1         2        3        4       5

                                  列

                                 讲台

想一想：怎样快速确定教室里小明和王健的位置？

学生回答，老师引导学生用一个有序数对（列，排）来说明教室这个平面内点的位置.

教师下结论：数轴上的点与实数一一对应，平面内的点与实数对一一对应.

教师讲解：

1.介绍法国数学家笛卡儿与平面直角坐标系.

2.讲解平面直角坐标系的基本概念.

想一想：平面直角坐标系有哪些特征？

学生逐一回答，教师引导得出结论：1.两条数轴；2.互相垂直；3.原点重合；4.通常取向上、向右为正方向；5.单位长度一般取相同的.

二、由点的位置指出点的坐标

教师讲解： A点在平面直角坐标系中的坐标为(4, 2),记作：A（4，2），其中4是点A的横坐标，2是点A的纵坐标.

典型例题

例1　写出图中A、B、C、D、E各点的坐标.

解：

三、由点的坐标确定点的位置

典型例题

例2　在平面直角坐标系中，描出下列各点：

 A(3，4)，B(3，-2)，C(-1，-4)，D(-2，2)，E(2，0)， F(0，-3).

学生在平面直角坐标系中描出，并在教师的引导下得出由点的坐标确定点的位置的一般步骤：第一步，在x轴上找出表示横坐标的点,过该点作x轴的垂线；第二步，在y轴上找出表示纵坐标的点,过该点作y轴的垂线；第三步，两条垂线的交点就是已知坐标表示的点的位置.

四、平面直角坐标系内点的坐标特点

观察下列点的位置和坐标，你能发现什么特点？

学生思考回答，教师在学生答案的基础上指出：x轴和y轴把坐标平面分成     四个部分,分别叫做第一、二、三、四象限.象限是按“逆时针”方向排列的.坐标轴上的点，也就是x轴、y轴上的点不属于任何一个象限.

小组内部交流讨论并展示：完成下表思考                                            

    教师讲解：对于坐标系内的任意一点P，都有唯一的一个有序数对（x,y)和它对应；反之，对于任意一个有序数对（x,y)，在坐标平面内都有唯一的一点P和它对应.

课堂练习

1.写出图中点A,B,C,D,E,F的坐标.

2.在平面直角坐标系内，下列各点在第四象限的是（     ）

A.(2,1)     B.(-2,1)    C.(-3,-5)    D.(3,-5)

3.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在( 　　)

A.第一象限       B.第二象限    C.第三象限       D.第四象限

4.已知P点坐标为（a-1，a-5）.

  ①点P在x轴上，则a＝        ；

  ②点P在y轴上，则a＝       ；

  ③若a＝-3 ，则P在第       象限内；

  ④若a＝3，则点P在第       象限内.

5.若点P（x，y）在第四象限，|x|＝2，|y|＝3，则P点的坐标为                  .

6.已知点P的坐标为(2+a , 3a+4),且点P到两坐标轴的距离相等，求点P的坐标.

参考答案

1.A( -2，-2 )，B (-5，4 )，C(5，-4)，D(0，-3)，E(2,5)，F(-3，0).

2.D

3.B

4.5，1，三，四

5.（2，-3）

6.解：点P(2+a , 3a+4)到两坐标轴的距离相等，所以|2+a|＝|3a+4|，

即2+a＝3a+4或2+a+3a+4＝0，解得a＝-1或a＝ .

当a＝-1时,点P的坐标为(1,1)；当a＝时，点P的坐标为.

综上所述，点P的坐标为(1,1)或.

课堂小结

布置作业

教材5页练习1，2，3题

板书设计

第1课时 平面直角坐标系中的点

教学反思

教学反思

教学反思

教学反思