数学沪科版13.1 三角形中的边角关系教学ppt课件

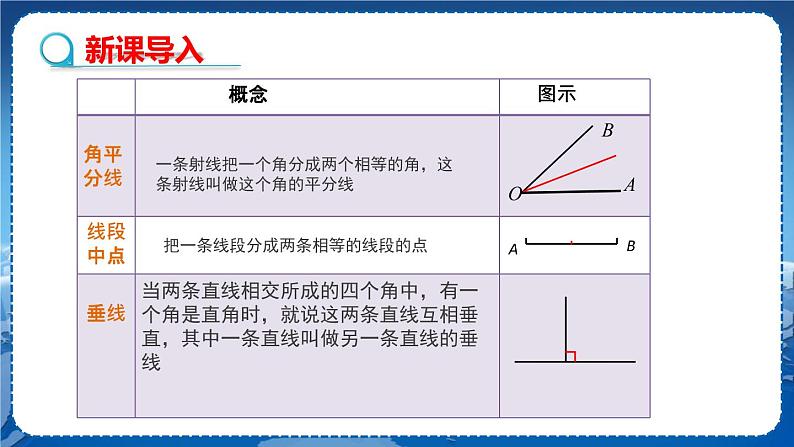
教学目标

1．使学生理解并掌握三角形的角平分线、中线、高线的定义，认识三角形的重心．

2．引导学生准确画出三角形的角平分线、中线、高线．

3．让学生理解并掌握三角形角平分线、中线、高线的性质．

教学重难点

重点：三角形的角平分线、中线、高线的定义及其性质．

难点：三角形的角平分线、中线、高线的画法及应用．

教学过程

导入新课

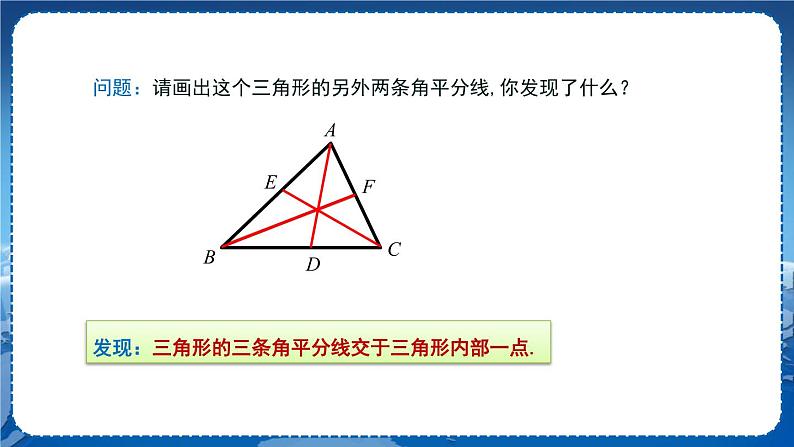
探究新知

一、三角形的角平分线

定义：三角形中，一个角的平分线与这个角对边相交，顶点与交点之间的线段叫做三角形的角平分线.

如图，在△ABC中，，线段AD 就是△ABC的角平分线.

想一想：三角形的角平分线与角的平分线相同吗?

不同，三角形的角平分线是线段，而角的平分线是射线.

问题：请画出这个三角形的另外两条角平分线,你发现了什么？

【小组内部交流】老师引导，学生发现规律：三角形的三条角平分线交于三角形内部一点.

例1 在△ 中，已知∠ ＝ ，分别是∠，∠ 的平分线，且BE，CF相交于点. ∠，求∠ 的度数.

解：因为 平分∠，∠ ＝21°，

所以∠＝＝2×21°＝42°.

因为∠+∠+∠ ＝180°，∠＝50°，

所以∠＝180°-50°-42°＝88°.

因为 平分∠，

所以∠＝∠＝＝44°.

教师活动：巡视指导，精讲点拨.

学生活动：学生自己写出过程，小组内交流.

二、三角形的中线

定义：三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线.

如图，△ABC中，点D是BC的中点，AD是△ABC的边上的中线.

想一想：由三角形的中线能得到什么结论？

【小组内部交流】老师引导学生得出结论：(或为的中点）

问题：你能分别画出锐角三角形、直角三角形、钝角三角形的三条中线吗？观察它们中线的交点你会发现什么规律？

【分组动手操作】老师引导，学生发现规律：三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.

拓展： 如图所示，在△ABC中，AD是△ABC的中线，AE是△ABC的高．试判断△ABD和△ACD的面积有什么关系？你能发现什么规律？

解：相等，因为两个三角形等底同高，所以它们的面积相等.

规律：三角形的中线能将三角形的面积平分.

【小组内部交流】老师引导学生发现规律.

例2在△ABC中，AC＝5 cm，AD是△ABC的中线，若△ABD的周长比△ADC的周长大2 cm，则BA＝________.

解析：因为△ABD的周长＝ AB+BD+ AD ，DB＝DC，

△ADC的周长＝AC+DC+AD，

所以△ABD的周长△ADC的周长

＝（AB+BD+AD）-（（AC+DC+AD）

＝AB-AC＝2 cm.

又因为AC＝5 cm，

所以AB＝7 cm.

答案：7 cm.

三、三角形的高

定义：从三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线，也叫做三角形的高.

如图，从△ABC的顶点A向它的对边BC所在直线画垂线段AD，垂线段AD就是△ABC的边BC上的高.

注意:标明垂直的记号和垂足的字母.

1.锐角三角形的高

问题：(1) 你能画出这个三角形的三条高吗?

(2) 这三条高之间有怎样的位置关系？

(3) 锐角三角形的三条高是在三角形的内部还是外部?

【小组内部交流】学生操作，老师总结：锐角三角形的三条高交于一点；

锐角三角形的三条高都在三角形的内部.

2.直角三角形的高

问题：画出直角三角形的三条高,直角三角形的三条高又有怎样的位置关系?

AC边上的高是    BD    ；

直角边BC边上的高是     AB      ；

直角边AB边上的高是    BC      .

【小组内部交流】学生操作，老师总结：直角三角形的三条高交于直角顶点.

3.钝角三角形的高

问题： 画出钝角三角形的三条高,钝角三角形的三条高又有怎样的位置关系?

【小组内部交流】学生操作，老师总结：钝角三角形的三条高不相交于一点,钝角三角形的三条高所在直线交于一点.

归纳：

例3  如图，已知AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝40°，求∠ADB的度数．

解：因为AD是△ABC的角平分线，∠BAC＝60°， 

所以∠DAC＝∠BAD＝30°.

因为CE是△ABC的高，∠BCE＝40°，

所以∠B＝50°，

所以∠ADB＝180°-∠B-∠BAD

＝180°-30°-50°

＝100°.

教师活动：巡视指导，精讲点拨.

学生活动：学生自己写出过程，小组内交流.

例4  如图所示，在△ 中，∠，∠， 是边上的高，是∠ 的平分线. 求∠ 的度数.

解：在△ 中，∵ ∠＝ 38°，∠＝ 54°，

∴ ∠BAC ＝ 180°-∠B-∠C＝ 180°-38°-54°＝ 88°.

∵ 是∠的平分线，

∴ ∠＝ ∠ ＝×88°＝44°.

∵ 是 边上的高，∴ ∠＝90°.

在△ 中，∵ ∠ ＝ ，∠＝54°，

∴ ∠＝180°-∠-∠＝180°-90°-54°＝36°.

∴ ∠＝＝∠-∠＝44°-36°＝8°.

教师活动：巡视指导，精讲点拨.

学生活动：学生自己写出过程，小组内交流.

课堂练习

1.如图,在△ABC中, ∠1＝∠2，G为AD的中点，延长BG交 AC于E，F为AB上一点，CF交AD于H，判断下列说法的正误.

（1）AD是△ABE的角平分线.(      )

（2）BE是△ABD的边AD上的中线.(     )

（3）BE是△ABC的边AC上的中线.(     )

2.如图所示，在△中，分别是△，△的中线，△ 的面积是4 ，那么△ 的面积是（　　）

A.2.5     B.2     C.1.5     D.1

3.如图所示，在△ABC中，AB＝AC＝5，BC＝6， AD⊥BC于点D，且AD＝4，若点P在边AC上移动，则BP的最小值为____.

4.如图，在△ABC中，AB边上的高是____，BC边上的高是____；在△BCF中，CF边上的高是____.

5.在等腰三角形ABC 中，AB ＝ AC，一腰上的中线BD 将这个等腰三角形的周长分成12和6 两部分， 求这个等腰三角形的腰长及底边长.

6.如图,AE是 △ABC的角平分线.已知∠B＝45°,∠C＝60°,求∠BAE和∠AEB的度数.

参考答案

1．（1）×（2）×（3）×

2．B

3.

4. CE   AD   BC

5.解：设，则.

（1）当 ＝12，++＝6时，有＝12，

所以 ＝4，＝8.所以＝＝-8，＝6-4＝2.

（2）当＝12，＝6时，有 ＝6，

解得＝2，所以

所以 ＝4， ＝12-2＝10.

因为，所以此时不能构成三角形.

综上所述，等腰三角形的腰长为8，底边长为2.

6.解：∵AE是△ABC的角平分线，

∴∠CAE＝∠BAE＝∠BAC.

∵ ∠BAC+∠B+∠C＝180°,

∴∠BAC＝180°-∠B-∠C＝180°-45°-60°＝75°，∴ ∠BAE＝37.5°.

∵∠AEB+∠B+∠BAE＝180°，

∴∠AEB＝180°-37.5°-45°＝97.5°.

课堂小结

布置作业

P73练习

板书设计

三角形中几条重要线段

1.三角形的角平分线：(1)定义；(2)画法；(3)三角形的三条角平分线交于一点.

2..三角形的中线：(1)定义；(2)画法；(3)三角形的三条中线交于一点——重心．

3.三角形的高线：(1)定义；(2)画法；(3)三角形的三条高线交于一点.

教学反思

教学反思

教学反思

教学反思

教学反思

教学反思