初中数学沪科版八年级上册14.2 三角形全等的判定教学ppt课件

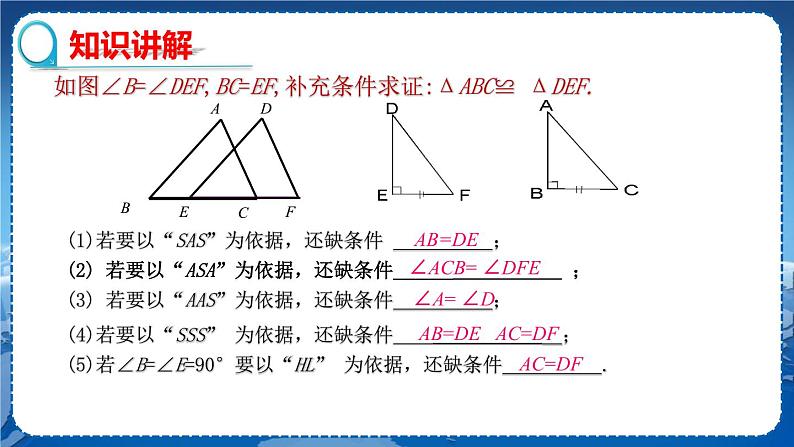
教学目标

1.多角度、多途径选择三角形全等的判定方法判定三角形全等.

2.会进行文字证明题的证明.

3.灵活运用全等三角形的性质证明线段或者角相等.

教学重难点

重点: 全等三角形的判定方法和性质的选择.

难点：文字题的证明.

教学过程

复习巩固

1.全等三角形的判定有哪些方法？

（1）已知两边

（2）已知一边一角

（3）已知两角

2.全等三角形的性质有哪些？

（1）对应边相等 ；（2）对应角相等

3.利用全等三角形性质证明两条线段或两个角相等

导入新课

探究新知

如图，∠B＝∠DEF,BC＝EF,补充条件求证：△ABC≌△DEF.

（1）若要以“SAS”为依据，还缺条件＿＿＿＿＿；

（2）若要以“ASA”为依据，还缺条件＿＿＿＿；

（3）若要以“AAS”为依据，还缺条件＿＿＿＿＿；

（4）若要以“SSS” 为依据，还缺条件＿＿＿＿＿；

（5）若∠B＝∠DEF＝90°要以“HL” 为依据，还缺条件＿＿＿＿＿.

思考：证明题的分析思路：①要证什么？

　　　　　　　　　      ②已有什么？

　　　　　　　　　      ③还缺什么？

　　　　　　　　　      ④创造条件.

合作探究

例1　已知:如图,AB＝CD,BC＝DA,E,F是AC上的两点,且AE＝CF.

求证:BF＝DE.

【问题探索】要说明BF﹦DE，由于BF、DE所在△ABE和△CBF中，只满足两边对应相等，需要证这两边的夹角相等，即∠1＝∠2，所以只需要证明△ADC≌△CBA即可，根据已知AB＝CD,BC＝DA及公共边可根据“SSS”判定全等.

证明：在△ABC和△CDA中,

∵

∴△ABC≌△CDA.(SSS)

∴∠1＝∠2.(全等三角形的对应角相等)

在△BCF与△DAE中,

∵

∴△BCF≌△DAE. (SAS)

∴BF＝DE.(全等三角形的对应边相等)

教师活动：引导学生分析题目中的条件，寻找证题方法，巡视指导，待学生完成后，指定一名学生黑板板演，老师给予点拨.

学生活动：学生自己写出过程，小组内交流.

【小组内部交流】

结论：对于一些利用全等证线段或者角相等的问题，有时需要证两次三角形全等才能解决.

例2　已知：如图，CD＝BE，DG⊥BC于点G，EF⊥BC于点F，且DG＝EF．连接BD，CE．

求证：BD＝CE．

【问题探索】要说明BD﹦CE，需要证所在三角形全等，由于BD、CE所在的三角形全等条件不具备，所以先根据已知条件CD＝BE，DG⊥BC于点G，EF⊥BC于点F，且DG＝EF．证明Rt△DGC≌Rt△EFB，从而得出∠BCD＝∠CBE，再根据“SAS”证明△BDC≌△CEB，从而得出结论.

证明：∵DG⊥BC，EF⊥BC，

∴∠DGC＝∠EFB＝90°．

在Rt△DGC和Rt△EFB中,

∴Rt△DGC≌Rt△EFB（HL），

∴∠BCD＝∠CBE.

∵BC＝CB，CD＝BE，

∴△BDC≌△CEB（SAS），

∴BD＝CE．

教师活动：巡视指导，精讲点拨.

学生活动：学生自己写出过程，小组内交流.

例3  证明：全等三角形对应边上的高相等.

已知:如图，△ABC≌△A′B′C′. AD，A′D′是△ABC 和△A′B′C′的高.求证：AD＝A′D′.

证明：△ABC≌△A′B′C′,(已知)

∴AB＝A′B′,∠B＝∠B′ .(全等三角形对应边相等、对应角相等)

∵AD,A′D′分别是△ABC, △A′B′C′的高，

∴∠ADB＝∠A′D′B′＝90°.(垂直的定义)

在△ABD与△A′B′D′中,  

∴△ABD≌△AB′D′.(AAS)

∴AD＝A′D′.(全等三角形的对应边相等)

教师活动：引导学生先根据题意画出符合条件的图形，再结合图形写出已知、求证，分析条件写出证明过程，巡视学生做题，及时点拨.

学生活动：在老师的指导下，画出图形，写出已知、求证并写出证明过程。小组内交流，并总结文字证明的证明过程分哪几步进行.

课堂练习

1.如图，已知点A，D，C，B在同一直线上，AD＝BC，DE∥CF，AE∥BF.

求证： CE∥DF．

2.已知：如图,P是BD上的任意一点，AB＝CB, AD＝CD.    

  求证:  PA＝PC.

3.证明:全等三角形对应边上的中线相等.

参考答案

1.证明：∵ DE∥CF，∴ ∠CDE＝∠FCD，

∴ ∠ADE＝∠BCF.(等角的补角相等)

∵ AE∥BF，∴ ∠A＝∠B.

在△ADE和△BCF中，

∴ △ADE≌△BCF（ASA）,∴ DE＝FC.(全等三角形对应边相等)

在△CDE和△DCF中，

∴ △CDE≌△DCF（SAS），

∴ ∠ECD＝∠FDC， (全等三角形对应角相等)

∴ CE∥DF．

2.证明：在△ABD和△CBD中，

    AB＝CB，（已知）

    AD＝CD，（已知）

    BD＝BD，（公共边）

  ∴ △ABD≌△CBD.(SSS)

  ∴ ∠ABD＝∠CBD.（全等三角形对应角相等）

  在△ABP和△CBP中 ，

    AB＝BC，（已知）

    ∠ABP＝∠CBP，（已证）

    BP＝BP，（公共边）

∴  △ABP≌△CBP.(SAS)

∴ PA＝PC.（全等三角形对应边相等）

3.已知:如图，△ABC≌△A′B′C′. AD,A′D′是△ABC 和△A′B′C′的中线.求证:AD＝A′D′.

证明：∵△ABC≌△A′B′C′,(已知)

∴ AB＝A′B′，∠B＝∠B′，BC＝B′C′ .(全等三角形对应边相等、对应角相等)

∵ AD,A′D′分别是△ABC, △A′B′C′的中线，

∴DB＝BC,D′B′＝B′C′,即DB＝D′B′.

在△ABD与△A′B′D′中,

AB＝A′B′,(已证)

∠B＝∠B′,(已证)

DB＝D′B′,(已证)

∴△ABD≌△A′D′B′.(SAS)

∴AD＝A′D′.(全等三角形的对应边相等)

课堂小结

1.利用三角形全等证明线段或者角相等时，有时需要两个全等.

2.文字证明题的一般格式

（1）先根据题意画出图形；

（2）结合题意和所画的图形，写出已知、求证；

（3）写出证明过程.

布置作业

教材P110练习1,2,3.

板书设计

三角形全等的判定和性质

1.利用双全等三角形证明线段或者角相等.

2.文字证明题的证明.

教学反思

教学反思

教学反思

教学反思

教学反思