2023年安徽省滁州市来安县九年级中考一模数学试卷(含答案)
展开来安县2023届九年级“一模”试卷
数学试题
注意事项:
1.你拿到的试卷满分150分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A、B、C、D、四个选项,其中只有一个是正确的。
1.下列为负数的是( )
A. B. C. D.0
2.安徽2022年新建5G基站25000座以上,其中数据25000用科学记数法表示为( )
A. B. C. D.
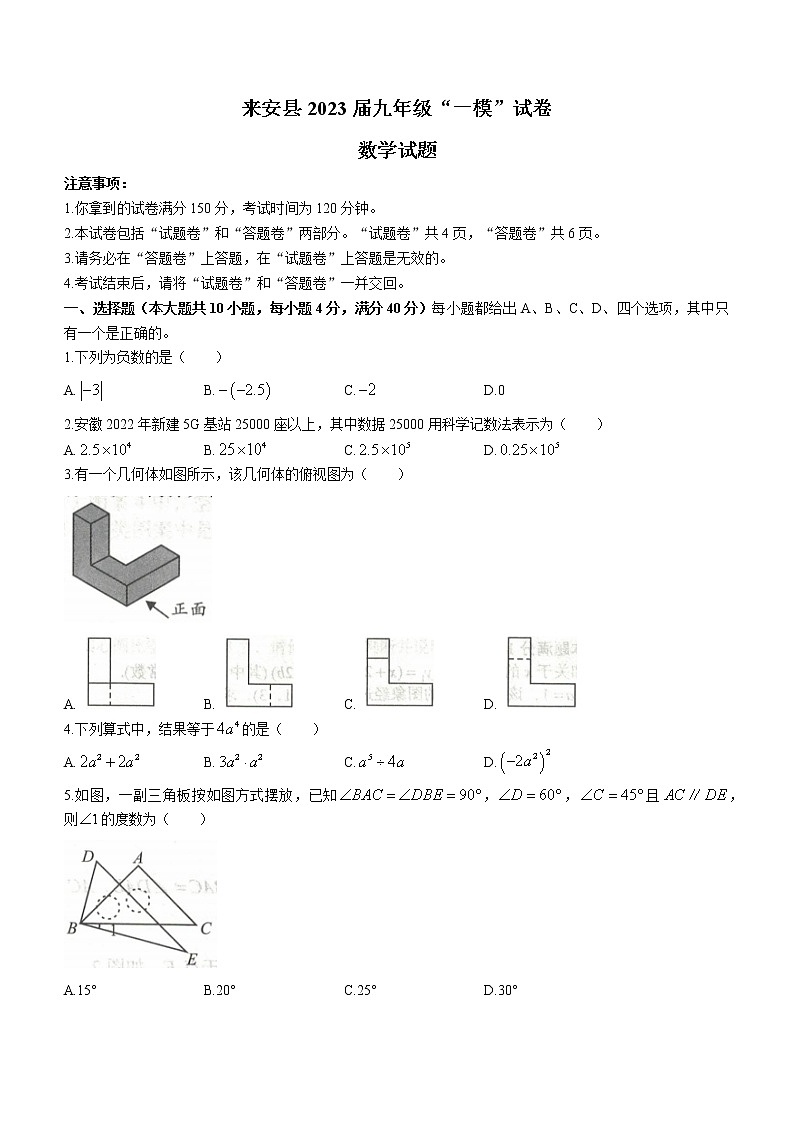
3.有一个几何体如图所示,该几何体的俯视图为( )
A. B. C. D.
4.下列算式中,结果等于的是( )
A. B. C. D.
5.如图,一副三角板按如图方式摆放,已知,,且,则的度数为( )
A.15° B.20° C.25° D.30°
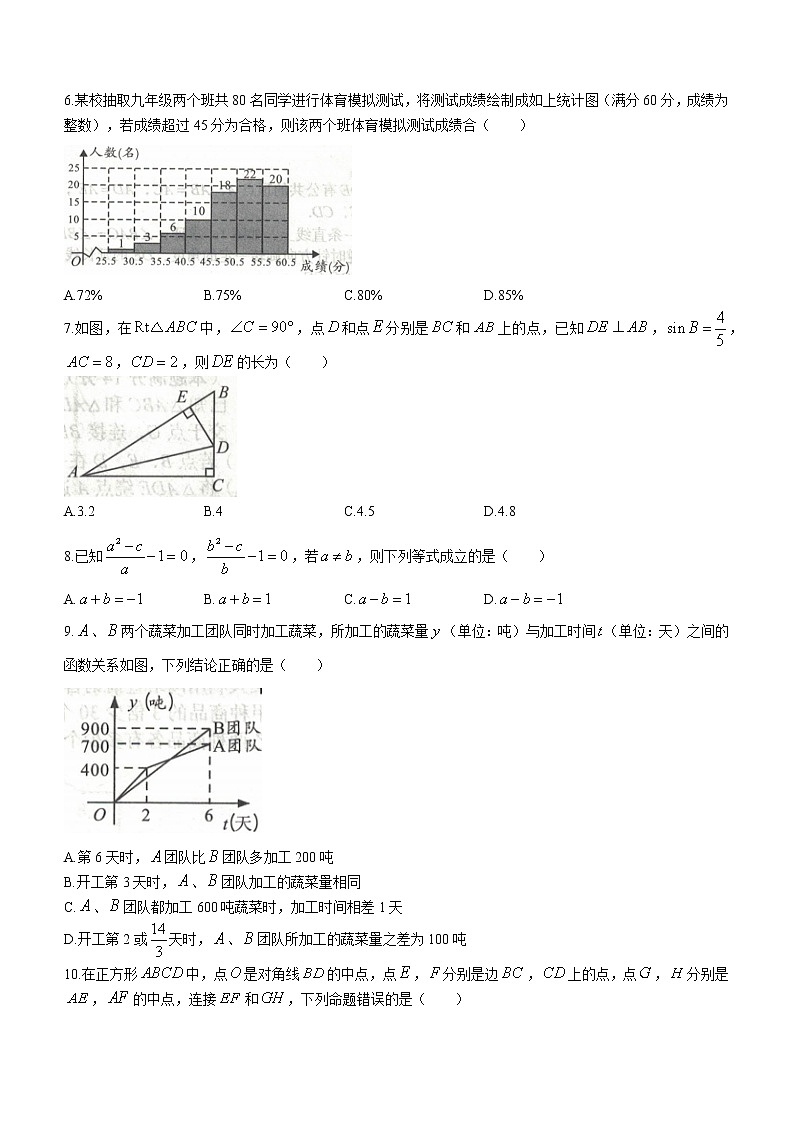
6.某校抽取九年级两个班共80名同学进行体育模拟测试,将测试成绩绘制成如上统计图(满分60分,成绩为整数),若成绩超过45分为合格,则该两个班体育模拟测试成绩合( )
A.72% B.75% C.80% D.85%
7.如图,在中,,点和点分别是和上的点,已知,,,,则的长为( )
A.3.2 B.4 C.4.5 D.4.8
8.已知,,若,则下列等式成立的是( )
A. B. C. D.
9.、两个蔬菜加工团队同时加工蔬菜,所加工的蔬菜量(单位:吨)与加工时间(单位:天)之间的函数关系如图,下列结论正确的是( )
A.第6天时,团队比团队多加工200吨
B.开工第3天时,、团队加工的蔬菜量相同
C.、团队都加工600吨蔬菜时,加工时间相差1天
D.开工第2或天时,、团队所加工的蔬菜量之差为100吨
10.在正方形中,点是对角线的中点,点,分别是边,上的点,点,分别是,的中点,连接和,下列命题错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算:______.
12.在一个三角形中,有两边长分别是1和5,已知第三边长为整数,则第三边长为______.
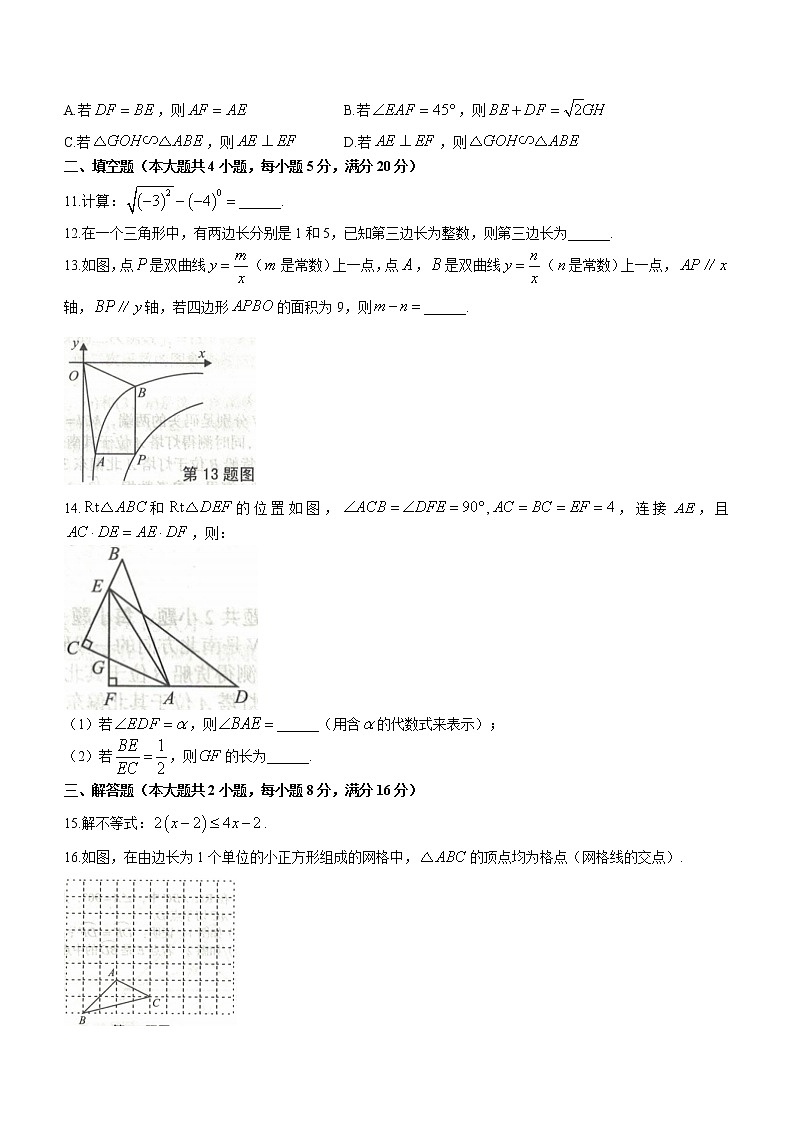
13.如图,点是双曲线(是常数)上一点,点,是双曲线(是常数)上一点,轴,轴,若四边形的面积为9,则______.
14.和的位置如图,,,连接,且,则:
(1)若,则______(用含的代数式来表示);
(2)若,则的长为______.
三、解答题(本大题共2小题,每小题8分,满分16分)
15.解不等式:.
16.如图,在由边长为1个单位的小正方形组成的网格中,的顶点均为格点(网格线的交点).
(1)将先向上平移6个单位,再向右平移5个单位,得到,请画出;
(2)以点为旋转中心,将按顺时针方向旋转90°,得到,请画出.
四、解答题(本大题共2小题,每小题8分,满分16分)
17.某人利用网络直播销售甲、乙两种商品,预计用4600元购进一批商品,其中乙种商品的个数是甲种商品的3倍少30个,甲、乙两种商品的单价分别为20元个、30元/个.求这一批商品中甲、乙两种商品各有多少个?
18.如图,小明设计如下的正方形图案,外一层是空心圆,内部全是实心圆,归纳图案中的规律,完成下列任务.
(1)图案4中,空心圆有______个;图案中实心圆有______个时,空心圆有______个;
(2)此类图案中是否存在实心圆比空心圆多8个,请你作出判断并说明理由.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.如图,线段是南北方向的一段码头,点和点分别是码头的两端,海里,某一时刻在点处测得货船位于其北偏东75°的方向上,同时测得灯塔位于其南偏东30°方向上,在点处测得灯塔位于其北偏东75°方向上,已知货船位于灯塔北偏东30°方向上,求此时货船距灯塔的距离的长(最终结果精确到0.1海里,参考数据:,,).
20.在中,,点是斜边上一点,以为直径作交于点,与切于点.
(1)如图1,证明:;
(2)如图2,若点是的中点,,求的长.
六、(本题满分12分)
21.如图,某同学在物理课中设计了两种控制小灯泡的电路图,电源、小灯泡、开关和线路都能正常工作,按要求完成下列问题:
(1)如图1,电路图中有3个开关、、,随意闭合2个开关,求小灯泡能发光的概率;
(2)如图2,电路图中有2个开关、,两个开关中间有三条导线,每次旋转开关都能接通一条导线,若随意调整开关、,求小灯炮发光的概率.
七、(本题满分12分)
22.已知关于的二次函数(其中,为常数).
(1)若,该二次函数的图像经过点,求;
(2)若.
①若和是该二次函数图象上的点,比较和的大小;
②设一次函数,当函数的图象经过点时,探索与之间的数量关系,并加以推理.
八、(本题满分14分)
23.已知和有公共的顶点,,,且.与相交于点,连接,.
(1)若点,,在一条直线上,如图1,求证:;
(2)将绕点逆时针方向旋转一定的角度,的延长线交于点,如图2.
①证明:;
②若,求的值.
来安县2023届九年级“一模”试卷
数学试题参考答案及评分标准
一、选择题(本题共10小题,每题4分,共40分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | A | C | D | A | B | A | B | D | B |
8.B 由题中的等式,得①,②,由①-②,得,因式分解,得,即或,又,∴.
9.D 由函数图像易求得:A团队在的时段内,与之间的函数关系式是;B团队在的时段内,与之间的函数关系式是.当时,,,A团队比B团队少加工200吨,故选项A错误;
当,解得,即开工天后,A,B团队加工的蔬菜量相同,选项B错误;
当时,,得;,得,∴,即A,B团队都加工600吨蔬菜时,加工时间相差天,选项C错误;
当A团队比B团队多加工100吨时,则,得;当A团队比B团队少加工100吨时,,解得,即第2或天时,A、B团队所加工的蔬菜量之差为100吨,故选项D正确.
10.B 如图1,由正方形的性质,得,,又,则,∴,故选项正确;
如图2,以点为旋转中心将按逆时针方向旋转90°,得,则,,,又,∴,∴,∴,又,故选项B错误;
如图3,连接,则,∵,∴,,同理,,∴,,∴,∵,∴,∴,∴,∴,∴,故选项C正确;
∵,∴,∴,∵,∴,∵,∴,由选项C知,∴,选项D正确.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.2 12.5 13. 14.(1) (2)
(2)∵,,且,,∴,∴,又,,∴,∴,∵,,∴,设,∴,在中,利用勾股定理得,即,解得,∴.
三、解答题(本大题共2小题,每小题8分,满分16分)
15.解:去括号,得,
移项,得,
合并同类项,得,
系数化为1,得.
16.解:(1)如图所示;(2)如图所示.
四、解答题(本大题共2小题,毎小题8分,满分16分)
17.解:设甲种商品有个,则乙种商品有个,根据题意,得,
解得,则,
答:这批商品中甲种商品有50个,乙种商品有120个.
18.解:(1)20;,;
(2)存在,理由如下:
根据题意,得:,
整理,得,解得(舍去)或,
故第6个图案中实心圆比空心圆多8个.
五、解答题(本大题共2小题,每小题10分,满分20分)
19.解:在中,,
∴,则(海里).
在中,.
如图,由,得,则,
∴.
过点作于点.
在中,,则海里,
∴海里=3海里
在中,,则海里.
∴(海里).
答:此时货船距灯塔的距离约为4.7海里.
20.解:(1)证明:如图1,连接,.∵是的切线,∴,
又,∴,∴.
∵,∴,∴,∴;
(2)如图2,连接,.∵点是的中点,∴.
由(1)可知,∴,∴,则,
∴是等边三角形,,,
∴,∴,∴.
六、(本题满分12分)
21.解:(1)有三种情况:,;,;,;其中小灯泡能发光的有,;,;所以(小灯泡能发光);
(2)设三条导线左侧端口依次为,,,右侧端口依次为,,,由题意列表,得
| |||
由列表可知随意调整开关,有9种等可能结果,其中使得小灯炮发光有,,共有3种,故(小灯炮发光).
七、(本题满分12分)
22.解:(1)当时,,代入点,得,解得;
(2)①当时,则,
∴该二次函数的图象与轴的交点坐标为,,
∴该二次函数的对称轴为,
又该二次函数图像开口向上,,∴;
②由题意可知,
又,∴,
∵抛物线经过点,∴,
∴或.(也可以写成或.也可以写成或)
八、(本题满分14分)
23.解:(1)证明:∵,∴,即.
又,,∴,∴.
在和中,,,
∴,即;
(2)①∵和都是等腰三角形,,
∴,又,∴,
∴,即,又,∴;
(2)如图,连接.由(1)得,∴.
由(2)①,得,∴,,
又,∴,
∴,,即,
又是等腰直角三角形,∴,
∴.
2023年安徽省滁州市来安县中考二模数学试题(含答案): 这是一份2023年安徽省滁州市来安县中考二模数学试题(含答案),共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023年安徽省滁州市来安县中考二模数学试题(含答案): 这是一份2023年安徽省滁州市来安县中考二模数学试题(含答案),共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023年安徽省滁州市来安县中考数学一模试卷(含答案解析): 这是一份2023年安徽省滁州市来安县中考数学一模试卷(含答案解析),共19页。试卷主要包含了 下列为负数的是,5)C等内容,欢迎下载使用。












