2023年河南省安阳市林州市中考数学适应性试卷（含答案）

这是一份2023年河南省安阳市林州市中考数学适应性试卷（含答案），共27页。
2023年河南省安阳市林州市中考数学适应性试卷
一.选择题（每小题3分，共30分）
1．（3分）2022的倒数的相反数是（　　）
A． B．﹣ C．﹣2022 D．2022
2．（3分）神舟十五号飞船于2022年11月29日发射成功，将在远地点高度393000m的轨道上驻留6个月进行太空实验研究．将数字393000用科学记数法表示为（　　）
A．3.93×105 B．0.393×106 C．3.93×106 D．39.3×104
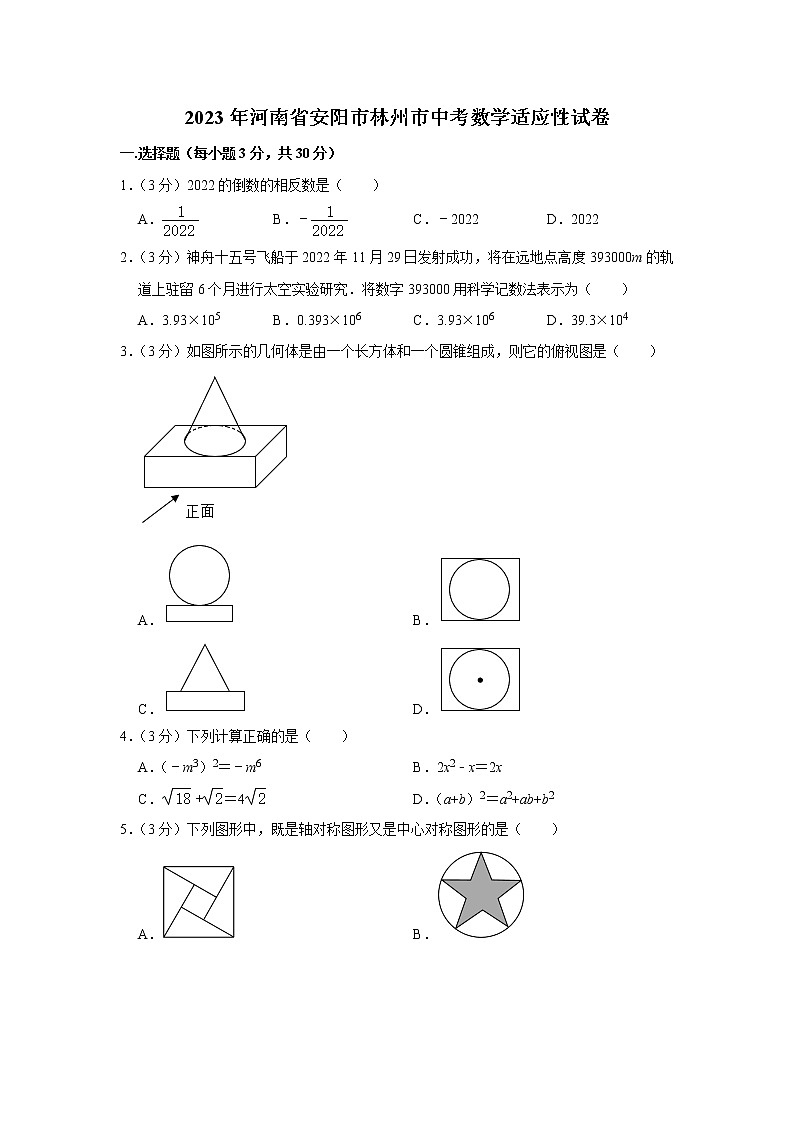
3．（3分）如图所示的几何体是由一个长方体和一个圆锥组成，则它的俯视图是（　　）

A． B．
C． D．
4．（3分）下列计算正确的是（　　）
A．（﹣m3）2＝﹣m6 B．2x2﹣x＝2x
C．＝4 D．（a+b）2＝a2+ab+b2
5．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
6．（3分）如图，把一张长方形纸条ABCD沿EF折叠，若∠BGD'＝x°，则∠1的度数为（　　）

A．（90﹣x）° B．（90﹣x）° C．（120﹣x）° D．（120﹣x）°
7．（3分）“读万卷书，行万里路．”某校为了丰富学生的阅历知识，坚持开展课外阅读活动，学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字．设该校七至九年级人均阅读量年均增长率为x，则可列方程为（　　）
A．100（1+x）2＝121
B．100（1+x%）2＝121
C．100（1+2x）＝121
D．100+100（1+x）+100（1+x）2＝121
8．（3分）如图是杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图，为了了解该天上午和下午的气温哪个更稳定，则应选择的统计量是（　　）

A．众数 B．平均数 C．方差 D．中位数
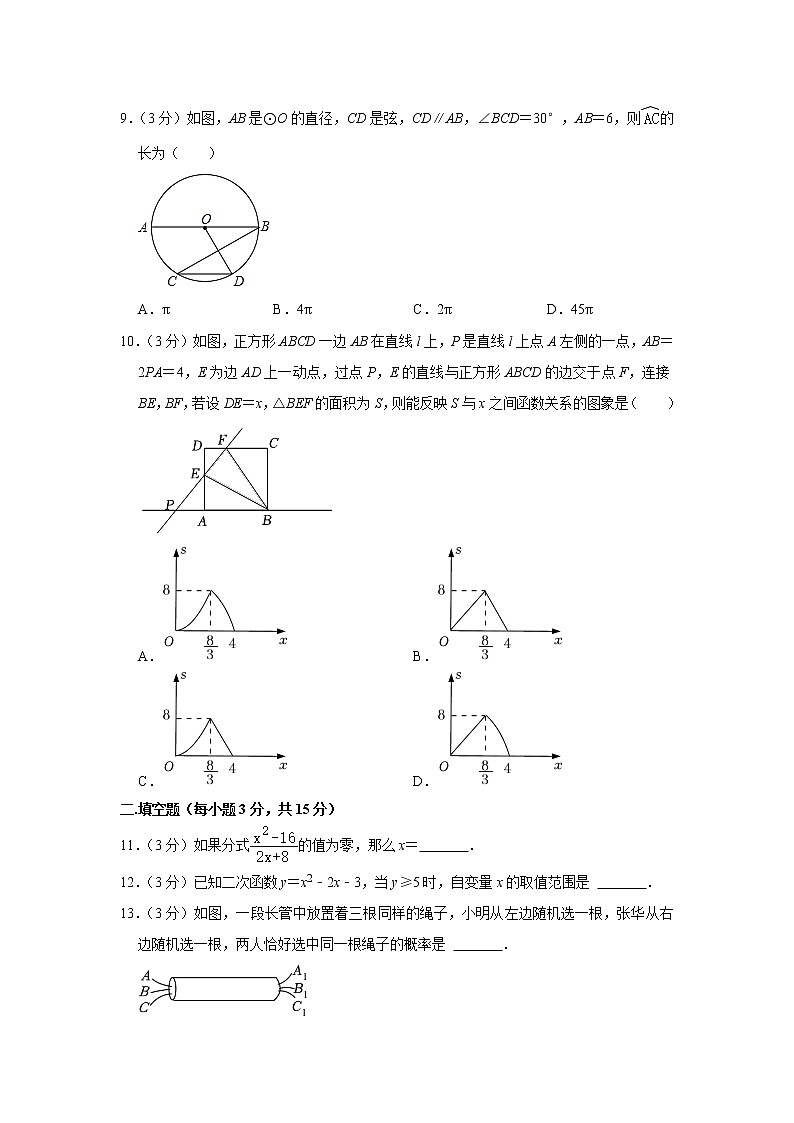
9．（3分）如图，AB是⊙O的直径，CD是弦，CD∥AB，∠BCD＝30°，AB＝6，则的长为（　　）

A．π B．4π C．2π D．45π
10．（3分）如图，正方形ABCD一边AB在直线l上，P是直线l上点A左侧的一点，AB＝2PA＝4，E为边AD上一动点，过点P，E的直线与正方形ABCD的边交于点F，连接BE，BF，若设DE＝x，△BEF的面积为S，则能反映S与x之间函数关系的图象是（　　）

A． B．
C． D．
二.填空题（每小题3分，共15分）
11．（3分）如果分式的值为零，那么x＝　 　．
12．（3分）已知二次函数y＝x2﹣2x﹣3，当y≥5时，自变量x的取值范围是 　 　．
13．（3分）如图，一段长管中放置着三根同样的绳子，小明从左边随机选一根，张华从右边随机选一根，两人恰好选中同一根绳子的概率是 　 　．

14．（3分）如图，扇形的圆心角∠AOB＝60°，半径为3cm．如果点C、D是AB的三等分点，图中所有阴影部分的面积之和是 　 　cm2．

15．（3分）如图，点E，F在正方形ABCD的对角线AC上，AC＝10，AE＝CF＝3，则四边形BFDE的面积为 　 　．

三.解答题（本大题共8小题，共75分）
16．（9分）（1）计算：．
（2）解不等式组，并写出它的正整数解．
17．（10分）为了解某校九年级学生科背知识竞赛的情况，现从中随机抽取部分学生的成绩，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：
（Ⅰ）本次随机抽样调查的学生人数为 　 　，图①中的m的值为 　 　；
（Ⅱ）求本次抽样调查获取的样木数据的众数、中位数和平均数；
（Ⅲ）若该校九年级共有学生1000人，如果竞赛成绩达到28分（含28分）及以上为优秀，请估计该校九年级学生在木次科皆竞赛中成绩优秀的人数．
18．（9分）如图，平面直角坐标系中，反比例函数y＝（n≠0）与一次函数y＝kx+b、k≠0）的图象相交于点A（1，m），B（﹣3，﹣1）两点．
（1）求反比例函数与一次函数的解析式；
（2）直接写出kx+b＞的解集；
（3）已知直线AB与y轴交于点C，点P（1，0）是x轴上一动点，作PQ⊥x轴交反比例函数图象于点Q，当以C，P，Q，O为顶点的四边形的面积等于2时，求t的值．

19．（9分）如图，某水渠的横断面是以AB为直径的半圆O，其中水面截线MN∥AB．嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°，点M的俯角为7°．已知爸爸的身高为1.7m．
（1）求∠C的大小及AB的长；
（2）请在图中画出线段DH，用其长度表示最大水深（不说理由），并求最大水深约为多少米（结果保留小数点后一位）．
（参考数据：tan76°取4，取4.1）

20．（9分）如图，BC为⨀O的直径，A为⨀O上一点，作∠BAC的平分线交⨀O于点D．过点D作⨀O的切线，交AC的延长线于点E．
（1）求证：DE∥BC；
（2）若AB＝8，AC＝6，求DE的长．

21．（9分）某超市采购了两批同样的冰墩墩挂件，第一批花了3300元，第二批花了4000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进25个，
（1）求第二批每个挂件的进价；
（2）两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？
22．（10分）已知二次函数y＝mx2﹣2mx﹣3（m≠0）．
（1）若该二次函数的最小值为﹣4，求这个二次函数的解析式；
（2）当m＞0且n≤x≤1时，函数值y的取值范围是﹣6≤y≤5﹣n，求n的值；
（3）在（2）的条件下，将此抛物线平移，且使其顶点始终在直线y＝﹣x﹣1上，求平移后所得抛物线与y轴交点纵坐标的最小值．
23．（10分）【操作与发现】
如图①，在正方形ABCD中，点N，M分别在边BC、CD上．连接AM、AN、MN．∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而可得：DM+BN＝MN．

（1）【实践探究】在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是 　 　．
（2）如图②，在正方形ABCD中，点M、N分别在边DC、BC上，连接AM、AN、MN，∠MAN＝45°，若tan∠BAN＝，求证：M是CD的中点．
（3）【拓展】如图③，在矩形ABCD中，AB＝12，AD＝16，点M、N分别在边DC、BC上，连接AM、AN，已知∠MAN＝45°，BN＝4，则DM的长是 　 　．


2023年河南省安阳市林州市中考数学适应性试卷
（参考答案与详解）
一.选择题（每小题3分，共30分）
1．（3分）2022的倒数的相反数是（　　）
A． B．﹣ C．﹣2022 D．2022
【解答】解：2022的的倒数是，相反数是﹣．
故选：B．
2．（3分）神舟十五号飞船于2022年11月29日发射成功，将在远地点高度393000m的轨道上驻留6个月进行太空实验研究．将数字393000用科学记数法表示为（　　）
A．3.93×105 B．0.393×106 C．3.93×106 D．39.3×104
【解答】解：393000＝3.93×105．
故选：A．
3．（3分）如图所示的几何体是由一个长方体和一个圆锥组成，则它的俯视图是（　　）

A． B．
C． D．
【解答】解：俯视图是矩形中间有一个圆，圆与两个长相切，
故选：D．
4．（3分）下列计算正确的是（　　）
A．（﹣m3）2＝﹣m6 B．2x2﹣x＝2x
C．＝4 D．（a+b）2＝a2+ab+b2
【解答】解：A、（﹣m3）2＝m6，原式计算错误，故选项不符合题意；
B、2x2和x不是同类项，不能合并，原式计算错误，故选项不符合题意；
C、+＝3+＝4，计算正确，故选项符合题意；
D、（a+b）2＝a2+2ab+b2，原式计算错误，故选项不符合题意．
故选：C．
5．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【解答】解：A．原图不是轴对称图形，是中心对称图形，故此选项不合题意；
B．原图是轴对称图形，不是中心对称图形，故此选项不合题意；
C．原图是轴对称图形，不是中心对称图形，故此选项不合题意；
D．原图既是轴对称图形又是中心对称图形，故此选项符合题意；
故选：D．
6．（3分）如图，把一张长方形纸条ABCD沿EF折叠，若∠BGD'＝x°，则∠1的度数为（　　）

A．（90﹣x）° B．（90﹣x）° C．（120﹣x）° D．（120﹣x）°
【解答】解：∵四边形ABCD为长方形，
∴AD∥BC，
∴∠DEF＝∠1，
由翻折可知，∠DEF＝∠D'EF，
∵∠EGF＝∠BGD'＝x°，
∴x°+∠1+∠1＝180°，
∴∠1＝（90﹣x）°．
故选：B．
7．（3分）“读万卷书，行万里路．”某校为了丰富学生的阅历知识，坚持开展课外阅读活动，学生人均阅读量从七年级的每年100万字增加到九年级的每年121万字．设该校七至九年级人均阅读量年均增长率为x，则可列方程为（　　）
A．100（1+x）2＝121
B．100（1+x%）2＝121
C．100（1+2x）＝121
D．100+100（1+x）+100（1+x）2＝121
【解答】解：设该校七至九年级人均阅读量年均增长率为x，
根据题意得100（1+x）2＝121．
故选：A．
8．（3分）如图是杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图，为了了解该天上午和下午的气温哪个更稳定，则应选择的统计量是（　　）

A．众数 B．平均数 C．方差 D．中位数
【解答】解：为了了解该天上午和下午的气温哪个更稳定，应选择的统计量是方差，
故选：C．
9．（3分）如图，AB是⊙O的直径，CD是弦，CD∥AB，∠BCD＝30°，AB＝6，则的长为（　　）

A．π B．4π C．2π D．45π
【解答】解：连接OC，如图：
∵AB是⊙O的直径，
∴OA＝AB＝3，
∵CD∥AB，
∴∠ABC＝∠BCD＝30°，
∴∠AOC＝2∠ABC＝60°，
∴的长为＝π；
故选：A．

10．（3分）如图，正方形ABCD一边AB在直线l上，P是直线l上点A左侧的一点，AB＝2PA＝4，E为边AD上一动点，过点P，E的直线与正方形ABCD的边交于点F，连接BE，BF，若设DE＝x，△BEF的面积为S，则能反映S与x之间函数关系的图象是（　　）

A． B．
C． D．
【解答】解：AB＝2PA＝4，
∴AB＝4，AP＝2，PB＝4+2＝6，
∵四边形ABCD是正方形，
∴AB＝AD＝BC＝CD＝4，
点F在边CD上时，DE＝x，AE＝4﹣x，
∴S＝S△BPF﹣S△BPE＝×6×4﹣×6（4﹣x）＝3x，
点F与点C重合时时，

S＝×4×4＝8，
∵四边形ABCD是正方形，
∴AD∥BC，
∴，
∴，解得x＝，
点F在边BC上时，

∵AD∥BC，
∴，即，
∴BF＝12﹣3x，
∴S＝×4（12﹣3x）＝24﹣6x，
∴当x＜时，S＝3x，当x＝时，S＝8，当＜x＜4时，S＝24﹣6x，
∴能反映S与x之间函数关系的图象是B，
故选：B．
二.填空题（每小题3分，共15分）
11．（3分）如果分式的值为零，那么x＝　4　．
【解答】解：，
根据题意，有：，
解得：x＝4，
故答案为：4．
12．（3分）已知二次函数y＝x2﹣2x﹣3，当y≥5时，自变量x的取值范围是 　x≥4或x≤﹣2　．
【解答】解：∵二次函数y＝x2﹣2x﹣3，
∴抛物线开口向上，对称轴为直线x＝﹣＝1，
∴当x＜1时，y随x的增大而减小；当x＞1时，y随x的增大而增大，
当y＝5时，则x2﹣2x﹣3＝5，即x2﹣2x﹣8＝0，
解得：x＝4或x＝﹣2，
∴当y≥5时，自变量x的取值范围是x≥4或x≤﹣2，
故答案为：x≥4或x≤﹣2．
13．（3分）如图，一段长管中放置着三根同样的绳子，小明从左边随机选一根，张华从右边随机选一根，两人恰好选中同一根绳子的概率是 　　．

【解答】解：画树状图如下：

共有9种等可能的结果，其中两人恰好选中同一根绳子的结果有3种，
∴两人恰好选中同一根绳子的概率为＝．
故答案为：．
14．（3分）如图，扇形的圆心角∠AOB＝60°，半径为3cm．如果点C、D是AB的三等分点，图中所有阴影部分的面积之和是 　π　cm2．

【解答】解：S扇形OAB＝＝π（cm2），
S阴影＝S扇形OAB＝×π＝π（cm2）．
故答案为：π．
15．（3分）如图，点E，F在正方形ABCD的对角线AC上，AC＝10，AE＝CF＝3，则四边形BFDE的面积为 　20　．

【解答】解：连接BD交AC于点O，

∵四边形ABCD为正方形，
∴OA＝OB＝OC＝OD，AC⊥BD，
又∵AE＝CF，
∴OE＝OF，
∴四边形BEDF为平行四边形，
∵EF垂直平分BD，
∴EB＝ED，
∴四边形BEDF是菱形，
∴BD＝AC＝10，
∵AE＝CF＝3，
∴EF＝4，
∴四边形BFDE的面积为BD•EF＝×10×4＝20．
故答案为：20．
三.解答题（本大题共8小题，共75分）
16．（9分）（1）计算：．
（2）解不等式组，并写出它的正整数解．
【解答】解：（1）原式＝2﹣2×+1﹣2
＝2﹣+1﹣2
＝﹣1；
（2），
解①得x＜，
解②得x≥﹣5，
不等式组的解集为﹣5≤x＜，
不等式组的正整数解为1，2．
17．（10分）为了解某校九年级学生科背知识竞赛的情况，现从中随机抽取部分学生的成绩，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：
（Ⅰ）本次随机抽样调查的学生人数为 　50　，图①中的m的值为 　24　；
（Ⅱ）求本次抽样调查获取的样木数据的众数、中位数和平均数；
（Ⅲ）若该校九年级共有学生1000人，如果竞赛成绩达到28分（含28分）及以上为优秀，请估计该校九年级学生在木次科皆竞赛中成绩优秀的人数．
【解答】解：（Ⅰ）9÷18%＝50（人），12÷50＝24%；
故答案为：50，24；
（Ⅱ）∵在这组数据中，28出现14次，出现的次数最多，
∴这组数据的众数是28；
将这组数据从小到大排列后，处在第25、26位的两个数都是28，因此中位数是28；
＝＝27.8；
答：平均数为27.8，中位数是28，众数是28；
（Ⅲ）1000×＝580人，
答：该校八年级学生在本次科普竞赛中成绩优秀的人数大约为580人．
18．（9分）如图，平面直角坐标系中，反比例函数y＝（n≠0）与一次函数y＝kx+b、k≠0）的图象相交于点A（1，m），B（﹣3，﹣1）两点．
（1）求反比例函数与一次函数的解析式；
（2）直接写出kx+b＞的解集；
（3）已知直线AB与y轴交于点C，点P（1，0）是x轴上一动点，作PQ⊥x轴交反比例函数图象于点Q，当以C，P，Q，O为顶点的四边形的面积等于2时，求t的值．

【解答】解：（1）点B（﹣3，﹣1）在反比例函数y＝的图象上，
∴n＝﹣3×（﹣1）＝3，
∴反比例函数的关系式为y＝，
当x＝1时，m＝＝3，
∴点A（1，3），
把A（1，3），B（﹣3，﹣1）代入y＝kx+b得，
，
解得，
∴一次函数的关系式为y＝x+2，
答：反比例函数关系式为y＝，一次函数的关系式为y＝x+2；
（2）由图象可知，不等式kx+b＞的解集为x＞1或﹣3＜x＜0；
（3）一次函数的关系式为y＝x+2与y轴的交点C（0，2），即OC＝2，
当以C，P，Q，O为顶点的四边形的面积等于2，
即S△COP+S△POQ＝2，而S△POQ＝|k|＝，
∴×|t|×2+＝2，
即|t|＝，
∴t＝．
因此t＝时，使以C，P，Q，O为顶点的四边形的面积等于2．
19．（9分）如图，某水渠的横断面是以AB为直径的半圆O，其中水面截线MN∥AB．嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°，点M的俯角为7°．已知爸爸的身高为1.7m．
（1）求∠C的大小及AB的长；
（2）请在图中画出线段DH，用其长度表示最大水深（不说理由），并求最大水深约为多少米（结果保留小数点后一位）．
（参考数据：tan76°取4，取4.1）

【解答】解：（1）∵嘉琪在A处测得垂直站立于B处的爸爸头顶C的仰角为14°，
∴∠CAB＝14°，∠CBA＝90°，
∴∠C＝180°﹣∠CAB﹣∠CBA＝76°，
∵tanC＝，BC＝1.7m，
∴tan76°＝，
∴AB＝1.7×tan76°＝6.8（m），
答：∠C＝76°，AB的长为6.8m；
（2）图中画出线段DH如图：

∵OA＝OM，∠BAM＝7°，
∴∠OMA＝∠OAM＝7°，
∵AB∥MN，
∴∠AMD＝∠BAM＝7°，
∴∠OMD＝14°，
∴∠MOD＝76°，
在Rt△MOD中，
tan∠MOD＝，
∴tan76°＝，
∴MD＝4OD，
设OD＝xm，则MD＝4xm，
在Rt△MOD中，OM＝OA＝AB＝3.4m，
∴x2+（4x）2＝3.42，
∵x＞0，
∴x＝≈0.82，
∴OD＝0.82m，
∴DH＝OH﹣OD＝OA﹣OD＝3.4﹣0.82＝2.58≈2.6（m），
答：最大水深约为2.6米．
20．（9分）如图，BC为⨀O的直径，A为⨀O上一点，作∠BAC的平分线交⨀O于点D．过点D作⨀O的切线，交AC的延长线于点E．
（1）求证：DE∥BC；
（2）若AB＝8，AC＝6，求DE的长．

【解答】（1）证明：如图1，连接OD，
∵DE是⊙O的切线，
∴OD⊥DE，
∴∠ODE＝90°，
∵BC为⨀O的直径，
∴∠BAC＝90°，
∵AD平分∠BAC，
∴∠BAD＝∠BAC＝×90°＝45°，
∵＝，
∴∠BOD＝2∠BAD＝2×45°＝90°，
∴∠BOD＝∠ODE，
∴DE∥BC；
（2）解：如图2，过点C作CF⊥DE于点F，连接OD，
∵∠BAC＝90°，AB＝8，AC＝6，
∴BC＝＝＝10，
∴OC＝OD＝5，
由（1）知：∠ODE＝∠BOD＝90°，
∴∠COD＝180°﹣∠BOD＝90°，
∵CF⊥DE，
∴∠CFD＝∠CFE＝90°，
∴∠COD＝∠ODE＝∠CFD＝90°，
∴四边形OCFD是矩形，
∴CF＝OD＝5，DF＝OC＝5，
∵DE∥BC，
∴∠E＝∠ACB，
∵∠CFE＝∠BAC＝90°，
∴△CEF∽△BCA，
∴＝，即＝，
∴EF＝，
∴DE＝DF+EF＝5+＝．


21．（9分）某超市采购了两批同样的冰墩墩挂件，第一批花了3300元，第二批花了4000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进25个，
（1）求第二批每个挂件的进价；
（2）两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？
【解答】解：（1）设第二批每个挂件进价是每个x元，
根据题意得＝﹣25，
解得x＝40，
经检验，x＝40是原方程的解，也符合题意，
∴x＝40，
答：第二批每个挂件进价是每个40元；
（2）设每个挂件售价定为m元，每周可获得利润W元，
∵每周最多能卖90个，
∴40+10×≤90，
解得m≥55，
根据题意得W＝（m﹣40）（40+10×）＝﹣10（m﹣52）2+1440，
∵﹣10＞0，
∴当m≥52时，y随x的增大而减小，
∵m≥55，
∴当m＝55时，W取最大，此时W＝﹣10×（55﹣52）2+1440＝1350．
∴当每个挂件售价定为55元时，每周可获得最大利润，最大利润是1350元．
22．（10分）已知二次函数y＝mx2﹣2mx﹣3（m≠0）．
（1）若该二次函数的最小值为﹣4，求这个二次函数的解析式；
（2）当m＞0且n≤x≤1时，函数值y的取值范围是﹣6≤y≤5﹣n，求n的值；
（3）在（2）的条件下，将此抛物线平移，且使其顶点始终在直线y＝﹣x﹣1上，求平移后所得抛物线与y轴交点纵坐标的最小值．
【解答】解：（1）∵y＝mx2﹣2mx﹣3＝m（x﹣1）2﹣m﹣3有最小值为﹣4，
∴，
解得：m＝1，
此时该二次函数的解析式是y＝x2﹣2x﹣3；

（2）∵y＝（x﹣1）2﹣4，
∴抛物线开口向上，的对称轴为x＝1，
∴当x＜1时，y随x的增大而减小．
又∵n≤x≤1时，函数值y的取值范围是﹣6≤y≤5﹣n，
∴，
解得m＝3，n＝﹣1或n＝（舍去），
故n的值为﹣1；

（3）∵m＝3，
∴设平移后的二次函数为y＝3x2+px+q，其顶点坐标为（﹣，q﹣），与y轴交点的纵坐标为q，
将（﹣，q﹣）代入y＝﹣x﹣1得：q﹣＝﹣1
∴q＝+﹣1＝（p+1）2﹣，
∵＞0，
∴p＝﹣1时，q取最小值，最大值为﹣，
∴平移后的抛物线与y轴交点的纵坐标最小值是﹣．
23．（10分）【操作与发现】
如图①，在正方形ABCD中，点N，M分别在边BC、CD上．连接AM、AN、MN．∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而可得：DM+BN＝MN．

（1）【实践探究】在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是 　12　．
（2）如图②，在正方形ABCD中，点M、N分别在边DC、BC上，连接AM、AN、MN，∠MAN＝45°，若tan∠BAN＝，求证：M是CD的中点．
（3）【拓展】如图③，在矩形ABCD中，AB＝12，AD＝16，点M、N分别在边DC、BC上，连接AM、AN，已知∠MAN＝45°，BN＝4，则DM的长是 　8　．

【解答】（1）解：∵四边形ABCD是正方形，
∴AB＝CD＝AD，∠BAD＝∠C＝∠D＝90°，
由旋转的性质得：△ABE≌△ADM，
∴BE＝DM，∠ABE＝∠D＝90°，AE＝AM，∠BAE＝∠DAM，
∴∠BAE+∠BAM＝∠DAM+∠BAM＝∠BAD＝90°，
即∠EAM＝90°，
∵∠MAN＝45°，
∴∠EAN＝90°﹣45°＝45°，
∴∠MAN＝∠EAN，
在△AMN和△AEN中，
，
∴△AMN≌△AEN（SAS），
∴MN＝EN，
∵EN＝BE+BN＝DM+BN，
∴MN＝BN+DM，
在Rt△CMN中，由勾股定理得：MN＝＝＝10，
则BN+DM＝10，
设正方形ABCD的边长为x，则BN＝BC﹣CN＝x﹣6，DM＝CD﹣CM＝x﹣8，
∴x﹣6+x﹣8＝10，
解得：x＝12，
即正方形ABCD的边长是12；
故答案为：12；
（2）证明：设BN＝m，DM＝n，
由（1）可知，MN＝BN+DM＝m+n，
∵∠B＝90°，tan∠BAN＝，
∴tan∠BAN＝＝，
∴AB＝3BN＝3m，
∴CN＝BC﹣BN＝2m，CM＝CD﹣DM＝3m﹣n，
在Rt△CMN中，由勾股定理得：（2m）2+（3m﹣n）2＝（m+n）2，
整理得：3m＝2n，
∴CM＝2n﹣n＝n，
∴DM＝CM，
即M是CD的中点；
（3）解：延长AB至P，使BP＝BN＝4，过P作BC的平行线交DC的延长线于Q，延长AN交PQ于E，连接EM，如图③所示：
则四边形APQD是正方形，
∴PQ＝DQ＝AP＝AB+BP＝12+4＝16，
设DM＝a，则MQ＝16﹣a，
∵PQ∥BC，
∴△ABN∽△APE，
∴＝＝＝，
∴PE＝BN＝，
∴EQ＝PQ﹣PE＝16﹣＝，
由（1）得：EM＝PE+DM＝+a，
在Rt△QEM中，由勾股定理得：（）2+（16﹣a）2＝（+a）2，
解得：a＝8，
即DM的长是8；
故答案为：8．