高中数学人教A版 (2019)必修 第一册4.4 对数函数精品课后复习题

这是一份高中数学人教A版 (2019)必修 第一册4.4 对数函数精品课后复习题，文件包含高中数学新教材同步讲义必修第一册44对数函数精讲教师版含解析docx、高中数学新教材同步讲义必修第一册44对数函数精讲学生版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
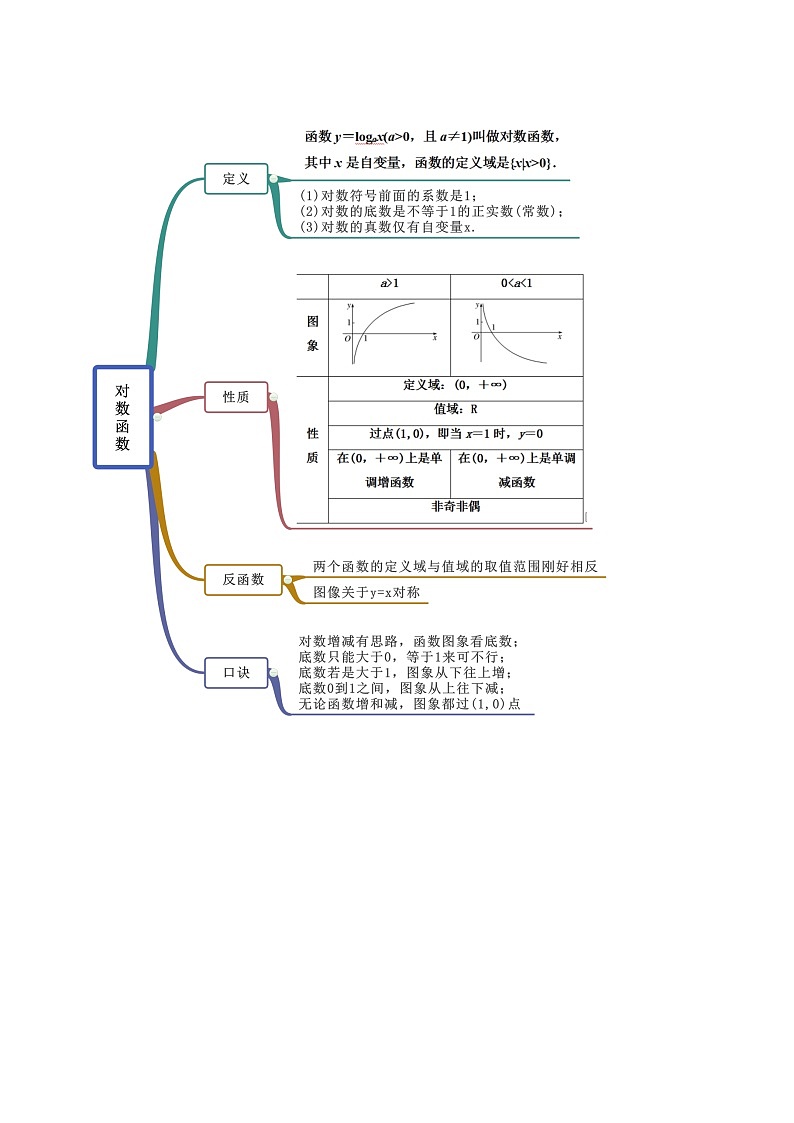
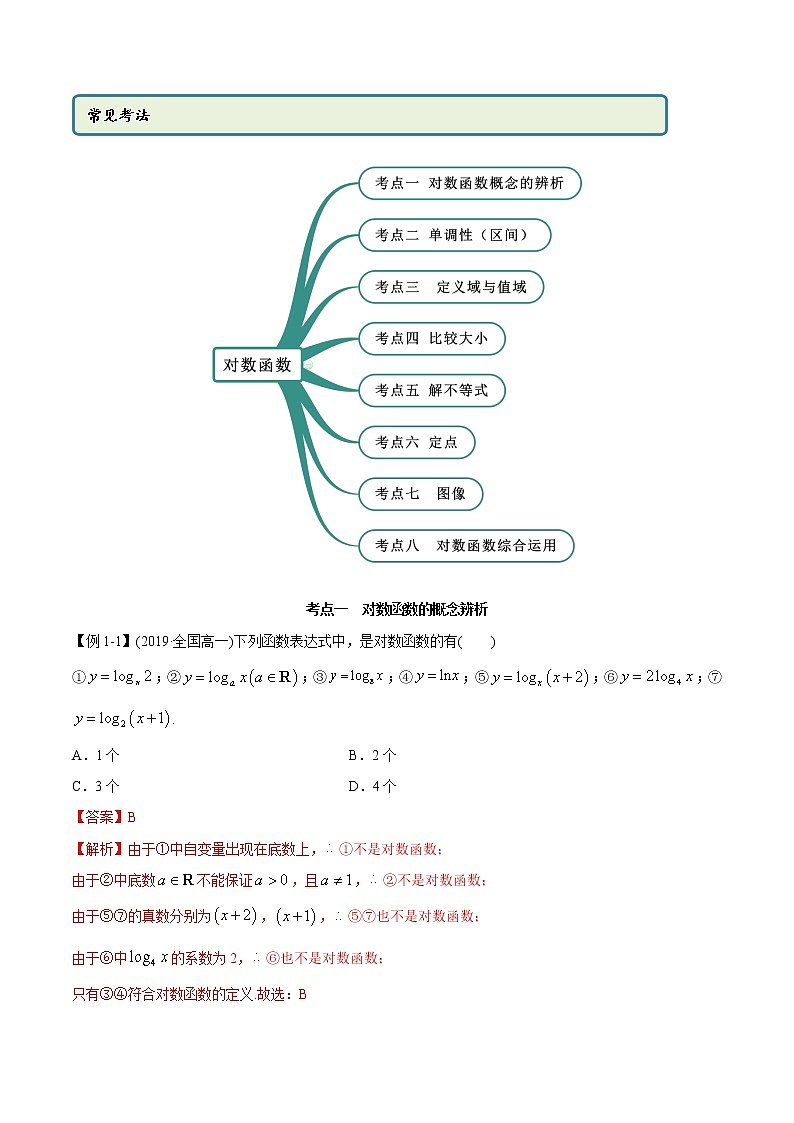
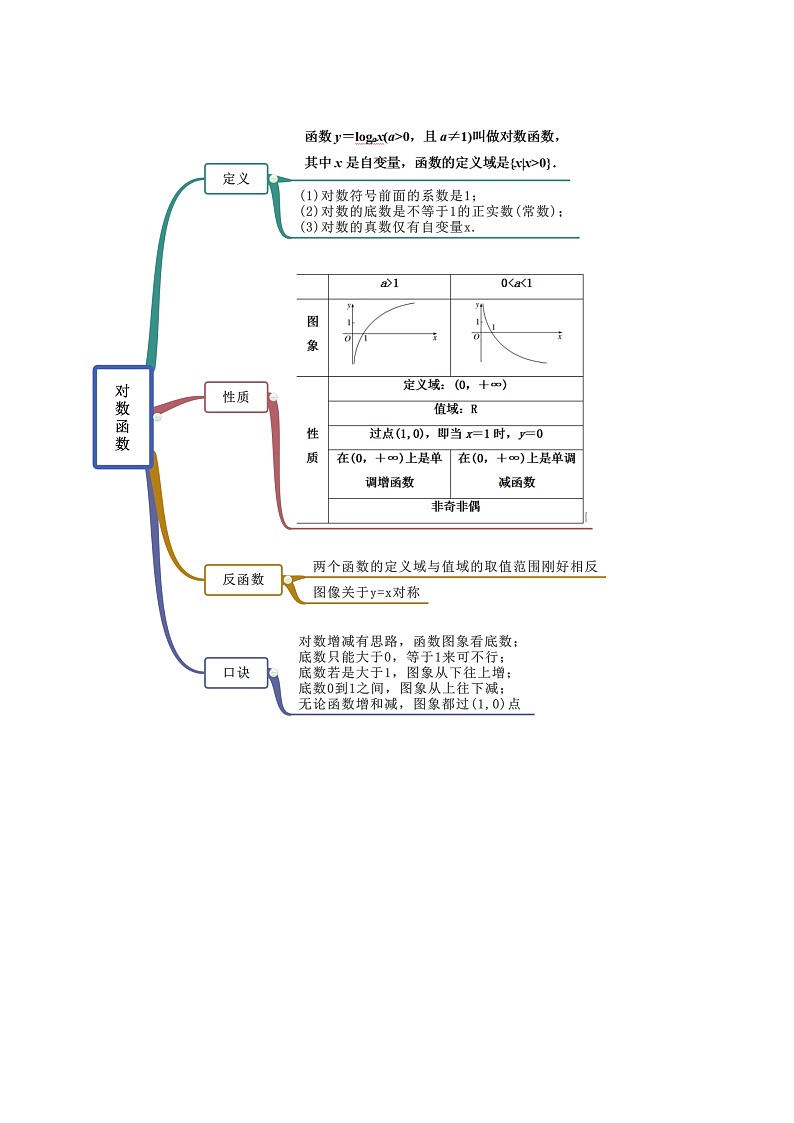
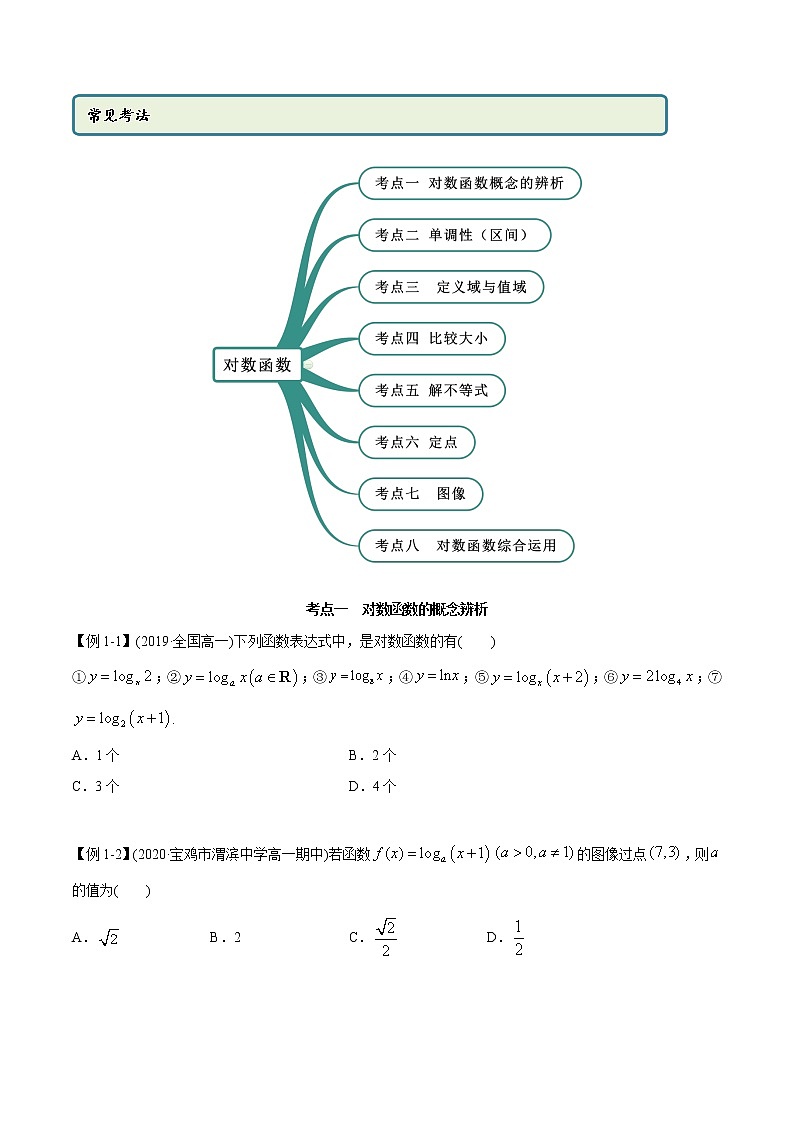
人教版高中数学必修一目录在社会发展的今天，数学发挥着不可替代的作用，也是学习和研究现代科学必不可少的基本工具。下面小编整理了《人教版高中数学必修一目录》，供大家参考！第一章 集合与函数概念1.1集合—阅读与思考，集合中元素的个数1.2函数及其表示—阅读与思考，函数概念的发展历程1.3函数的基本性质—信息技术应用，用计算机绘制函数图形第二章 基本初等函数（1）2.1指数函数—信息技术应用，借助信息技术探究指数函数的性质2.2对数函数—阅读与思考，对数的发明探究与发现，互为反函数的两个函数图像之间的关系第三章 函数的应用3.1函数与方程—阅读与思考，中外历史上的方程求解信息技术应用，借助信息技术求方程的近似解3.2函数模型及其应用—信息技术应用，收集数据并建立函数模型 4.4 对数函数            考点一  对数函数的概念辨析【例1-1】(2019·全国高一)下列函数表达式中，是对数函数的有(    )①；②；③；④；⑤；⑥；⑦.A．1个 B．2个C．3个 D．4个【答案】B【解析】由于①中自变量出现在底数上，①不是对数函数；由于②中底数不能保证，且，②不是对数函数；由于⑤⑦的真数分别为，，⑤⑦也不是对数函数；由于⑥中的系数为2，⑥也不是对数函数；只有③④符合对数函数的定义.故选：B【例1-2】(2020·宝鸡市渭滨中学高一期中)若函数的图像过点，则的值为(    )A． B．2 C． D．【答案】B【解析】由题, .故选：B【举一反三】1．(2020·全国高一课时练习)下列函数为对数函数的是(    )A．y＝logax＋1(a＞0且a≠1)           B．y＝loga(2x)(a＞0且a≠1)C．y＝log(a－1)x(a＞1且a≠2)             D．y＝2logax(a＞0且a≠1)【答案】C【解析】根据对数函数的定义，可得判定，只有函数且复数对数函数的概念，所以函数且是对数函数，而选项A、B、D中的函数只能是对数型函数，不是对数函数.故选：C.2．下列函数是对数函数的是(   )A． B．  C． D．  【答案】C【解析】由对数函数定义可以，本题选C．3．下列函数，是对数函数的是A．y=lg10x B．y=log3x2C．y=lnx D．y=log(x–1)【答案】C【解析】由对数函数的定义，形如y=logax(a>0，a≠1)的函数是对数函数，由此得到：y=lg10x=x，y==2、y=都不是对数函数，只有y=lnx是对数函数．故选C．4．(2020·全国高一课时练习)对数函数的图象过点M(16,4)，则此对数函数的解析式为(　　)A．y＝log4x B．y＝ xC．y＝ x D．y＝log2x【答案】D【解析】由于对数函数的图象过点M(16,4)，所以4＝loga16，得a＝2所以对数函数的解析式为y＝log2x，故选D.考点二  单调性(区间)【例2】(1)(2020·辽宁锦州·高二期末)函数的单调减区间是(    )A． B． C． D．(2)(2019·四川省新津中学高一月考)已知在上是增函数，则实数的取值范围是(    )A． B．C． D．【答案】(1)D(2)C【解析】由题：，，解得：，的减区间，即的减区间，对称轴为结合二次函数单调性，所以的减区间.故选：D(2)设， 在上是增函数，，即，解得， 实数的取值范围是 ，故选：C．【举一反三】1．(2019·小店·山西大附中高一期中)函数的单调递减区间为(   )A． B． C． D．【答案】A【解析】因为，所以，解得或 令，因为的图像开口向上，对称轴方程为 ，所以内函数在上单调递增，外函数单调递减，所以由复合函数单调性的性质可知函数的单调递减区间为故选A.2．函数y=是A．区间(–∞，0)上的增函数 B．区间(–∞，0)上的减函数C．区间(0，+∞)上的增函数 D．区间(0，+∞)上的减函数【答案】A【解析】如图所示，函数y=的图象与函数y=的图象关于y轴对称，所以函数y=是区间(–∞，0)上的增函数．故选A．3．(2020·全国)已知函数在上单调递增，则的取值范围是(    )A． B． C． D．【答案】D【解析】由得或所以的定义域为因为在上单调递增所以在上单调递增所以故选：D考点三  定义域和值域【例3】(1)(2020·永昌县第四中学高二期末(文))函数的定义域为(    )A． B． C． D．(2)(2019·新疆兵团第二师华山中学高二月考(文))函数的值域是(   ).A．R B． C． D．【答案】(1)C(2)B【解析】(1)要使得函数有意义，只需：且，解得.故函数定义域为.故选：.(2)恒成立，函数的定义域为设 由复合函数的单调性可知函数在定义域上先增后减，函数取到最大值即： 函数的值域为故选【举一反三】1．(2020·沭阳县修远中学高二期末)函数的定义域为(    )A． B． C． D．【答案】A【解析】函数的定义域满足：，解得.故选：A.2．(2020·湖南高新技术产业园区·衡阳市一中高三月考)已知函数的定义域是，则函数的定义域是________.【答案】【解析】由题意，函数的定义域是，即，则函数有意义，则满足 ，解得，解得，即函数的定义域是.故答案为：.3．(2019·北)若函数 则函数的值域是(   )A． B． C． D．【答案】A【解析】画出函数的图像如下图所示，由图可知，函数的值域为，故选A.考点四  比较大小【例4】(2020·全国高一课时练习)比较下列各组数中两个值的大小．(1)log23.4，log28.5；(2)log0.31.8，log0.32.7；(3)loga5.1，loga5.9(a>0，且a≠1)．【答案】(1)；(2)；(3)当时，；当时，.【解析】(1)根据对数函数在为单调递增函数，因为，所以.(2)根据对数函数在为单调递减函数，因为，所以.(3)根据对数函数的性质，可得：当时，函数在为单调递减函数，因为，所以；当时，函数在为单调递增函数，因为，所以.【举一反三】1．(2020·辽源市田家炳高级中学校高二期末(文))已知，，，则，，的大小关系是(    )A． B． C． D．【答案】A【解析】,,,,故选：A2．(2020·哈尔滨市第十二中学校高二期末(文))已知，，，则(    )A． B．C． D．【答案】A【解析】，，，所以，故选：A.3．(2020·贵州铜仁伟才学校高二期末(文))若，，，则(    )A． B．C． D．【答案】A【解析】因为，所以，故.故选：A.考点五  解不等式【例5】(2020·内蒙古集宁一中高二期末(文))不等式的解集是________.【答案】【解析】由在单调递减，因为，所以 ，解得，，即解集为.故答案为:【举一反三】1．(2020·安徽马鞍山)已知函数是定义域为的偶函数，在上单调递减，则不等式的解集是(    )A． B．(1，3) C． D．【答案】C【解析】因为的图象是由的图象向左平移2个单位，而的图象关于轴对称，故的图象关于直线对称.由在上单调递减可得在上单调递增，故即为，也就是，所以或，解得或，故选：C．2．(2020·湖北)已知函数是定义在上的奇函数，当时，，若实数满足，则的取值范围是(    )A． B． C． D．【答案】A【解析】当时，，，因为是定义在上的奇函数，所以，即.因此，作出的图象如下：在上单调递增，又，由得：，解得：.故选：A.3．(2019·山东省实验中学高三月考)已知函数 (>0且≠1)的图像过点(9，2)(1)求函数的解析式；(2)解不等式．【答案】(1)(2)【解析】(1)因为，所以，即 (2)因为单调递增，所以即不等式的解集是考点六  定点【例6】(2020·山东省枣庄市第十六中学高一期中)函数的图象恒过定点，(其中且)，则的坐标为__________.【答案】【解析】令，解得 ，所以 ，所以 的坐标为，故答案为：【举一反三】1.(2020·云南省玉溪第一中学高一期中)函数的图象必过定点(　　)A． B． C． D．【答案】A【解析】∵过定点， ∴， ，故图象必过定点．故选：A．2．(2019·重庆高一月考)函数(，且)的图象恒过点(   )A． B． C． D．【答案】B【解析】真数为1时，对数为0，所以令x=2，则f(x)=1，所以函数的图象过定点.考点七  图像【例7】(2020·哈尔滨市第十二中学校高二期末(文))函数(且)与函数(且)在同一直角坐标系内的图象可能是(    )A． B． C． D．【答案】A【解析】当时，和均为减函数，而的图象和的图象关于y轴对称，结合选项知A、B、C、D均错误；当时，和均为增函数，而的图象和的图象关于y轴对称，结合选项可得A正确.故选：A【举一反三】1．(2020·山东滨州·高二期末)函数的图象大致是(    )A． B．C． D．【答案】A【解析】,所以舍B;当时,单调递增，所以舍去CD，故选：A2．(2020·全国高一课时练习)函数y＝2log4(1－x)的图象大致是A． B． C． D．【答案】C【解析】函数的定义域为且单调递减，故选C.3.如图，若C1，C2分别为函数y＝logax和y＝logbx的图象，则(　　)A．0＜a＜b＜1                B．0＜b＜a＜1C．a＞b＞1                     D．b＞a＞1【答案】B【解析】作直线y＝1，则直线与C1，C2的交点的横坐标分别为a，b，易知0＜b＜a＜1.考点八  对数函数综合运用【例8】(2020·甘肃省会宁县第四中学高二期末(文))已知函数．(1)求的值；(2)求函数的定义域(3)判断函数的奇偶性，并证明.【答案】(1)；(2)；(3)偶函数，证明见解析．【解析】(1)令，则(2)由题意:，解得，故定义域为；(3)函数为偶函数证明：对任意，由偶函数的定义可得函数为偶函数   【举一反三】1．(2020·湖南桃江·高二期末)已知函数且.(1)求的定义域；(2)解关于的不等式.【答案】(1)当时，定义域为，当时，定义域为；(2).【解析】(1)由函数有意义得，∴当时，定义域为 ，当时，定义域为 .(2)∵在定义域内，∴∴单调递增，结合定义域可知：的解集为.2．(2020·山东省枣庄市第十六中学高一期中)已知函数，a常数.(1)若，求证为奇函数，并指出的单调区间；(2)若对于，不等式恒成立，求实数m的取值范围.【答案】(1)证明见解析，单调增区间为；(2).【解析】(1)证明：当时，.的定义域为.当时,.，∴在区间上是奇函数，的单调增区间为，.(2)由，得.令，若使题中不等式恒成立，只需要.由(1)知在上是增函数，所以.所以m的取值范围是.