沪科版22.2 相似三角形的判定教学课件ppt

这是一份沪科版22.2 相似三角形的判定教学课件ppt，文件包含2224pptx、上海科技版中学数学九年级上第22章相似形222相似三角形的判定第4课时教学详案docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
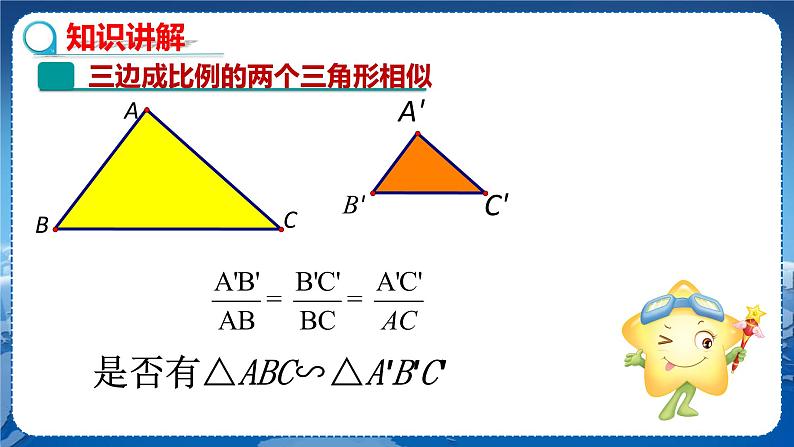
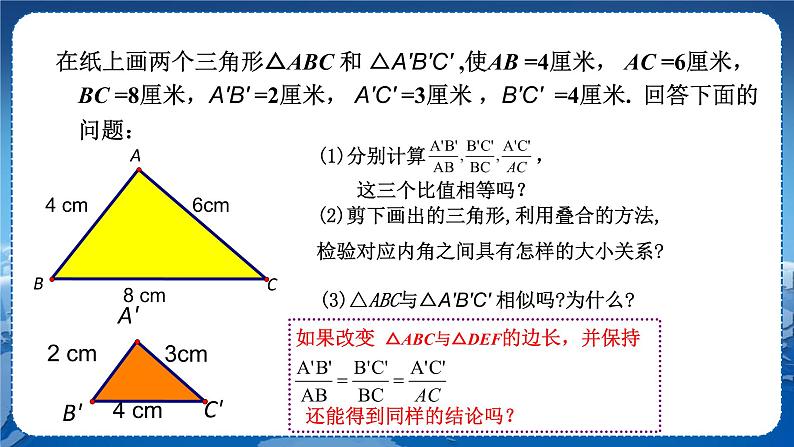
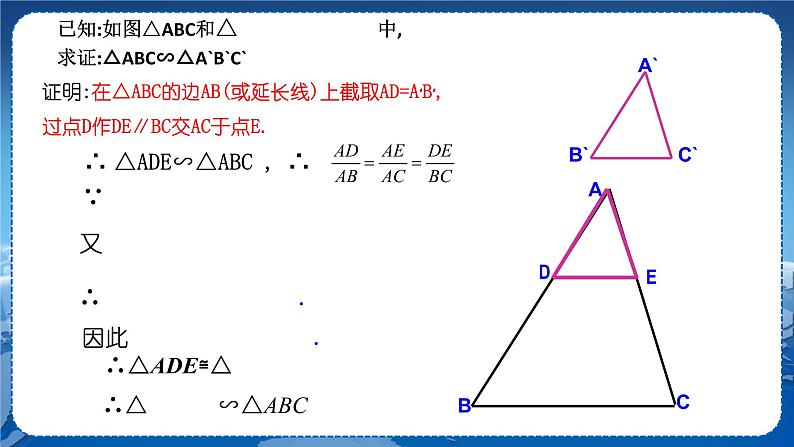
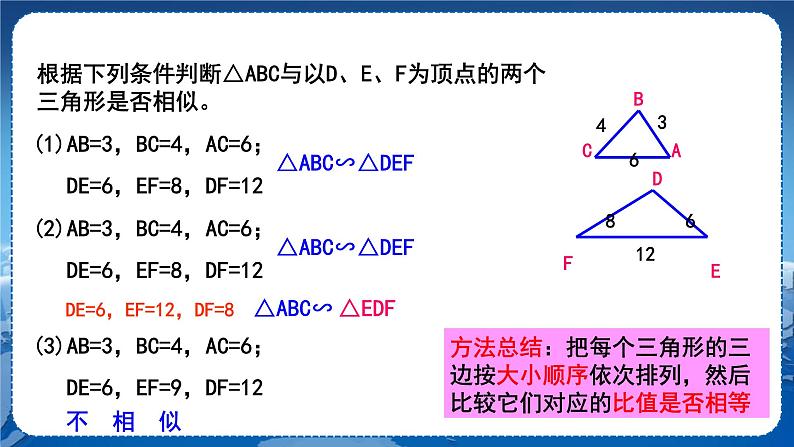
第22章  相似形22.2　相似三角形的性质第4课时　相似三角形的判定定理3教学目标1.经历三角形相似的判定方法“三边成比例的两个三角形相似”的探索过程.2.能运用上述判定方法判定两个三角形相似.教学重难点重点：理解“三边成比例的两个三角形相似”的判定方法.难点：会运用“三边成比例的两个三角形相似”的判定方法解决简单问题.教学过程复习回顾    我们学过哪些判定三角形相似的方法？探究新知若 ，是否有△ABC∽△A′B′C′？ 【互动】（小组讨论作图，教师引导总结结论）在纸上画两个三角形△ABC 和△A′B′C′，使AB＝4 cm，AC＝6 cm，BC＝8 cm，A′B′＝2 cm， A′C′＝3 cm，B′C′＝4 cm.回答下面的问题：(1)分别计算，这三个比值相等吗？(2)剪下画出的三角形，利用叠合的方法，检验对应内角之间具有怎样的大小关系?(3)△ABC与△A′B′C′相似吗?为什么?【思考】如果改变 △ABC与△A′B′C′的边长，并保持，还能得到同样的结论吗？ →△ABC∽△A′B′C′.三边对应成比例的两个三角形相似. 【推导】（用学过的知识，进行推导）已知：如图，在△ABC和△A′B′C′中，A′B′∶AB＝A′C′∶AC＝B′C′∶BC.求证：△ABC∽△A′B′C′.  解：已知：如图，在△ABC和△A′B′C′中，.求证：△ABC和∽A′B′C′.证明：在△ABC的边AB上截取AD＝A′B′，过点D作DE∥BC交AC于点E，∴ △ADE∽△ABC， .∵AD＝A′B′，∴ 又 ，∴ ， .因此DE＝B′C′，EA＝C′A′.∴ △ADE≌△A′B′C′.∴△A′B′C′∽△ABC. 【发现】如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似.判定定理3：如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似.简记为：三边成比例的两个三角形相似.  符号语言：在△ABC与△DEF中，∵ ，∴ △ABC∽△DEF. 【活动】根据下列条件判断△ABC与以D，E，F为顶点的两个三角形是否相似.（1）AB＝3，BC＝4，AC＝6；DE＝6，EF＝8，DF＝12.△ABC∽△DEF.（2）AB＝3，BC＝4，AC＝6；DE＝6，EF＝9，DF＝12.答案：（1）△ABC∽△DEF.（2）不相似. 【总结】把每个三角形的三边按大小顺序依次排列，然后比较它们对应的比是否相等.【探究】例1　如图，已知 .找出图中相等的角，并说明你的理由.解：∠BAC＝∠DAE，∠B＝∠D，∠C＝∠E，∠BAD＝∠CAE.理由如下：在△ABC与△ADE中，∵ ，∴ △ABC∽△ADE.∴ ∠BAC＝∠DAE，∠B＝∠D，∠C＝∠E.∵∠BAC-∠DAC＝∠DAE-∠DAC，∴ ∠BAD ＝∠CAE.【探究】例2　已知：如图，DE，DF，EF是△ABC的中位线.求证：△ABC∽△FED.证明：∵ DE，DF，EF是△ABC的中位线，∴ DE＝BC，DF＝AC，EF＝AB.∴，∴△ABC∽△FED. 例3 如图，在Rt△ABC和Rt△A′B′C′中，∠B＝∠B′＝90°，.求证：Rt△ABC∽Rt△A′B′C′.   课堂练习1.如图，已知△ABC与△DEF中，AB＝5，BC＝12，AC＝8，DE＝10，则当DF＝　　　，EF＝　　　时，△ABC∽△DEF.2.根据下列条件，判断△ABC与△A′B′C′是否相似，并说明理由.AB＝4 cm，BC＝6 cm，AC＝8 cm；A′B′＝12 cm，B′C′＝18 cm，A′C′＝24 cm.3.如图，在6×6的正方形方格中，△ABC与△DEF的顶点都在边长为1的小正方形的顶点上，（1）填空：BC＝________，AC＝________，EF＝________，DF＝________.（2）△ABC与△DEF相似吗？若相似，请给出证明，若不相似，请说明理由.   参考答案1.16　24  2.解：∵ ， ， ，∴，∴△ABC∽△A′B′C′.（三边成比例的两个三角形相似）3.解：（1）　（2）相似.证明：因为，所以△ABC∽△DEF.课堂小结 布置作业教材第85页习题22.2.  板书设计三边成比例的两个三角形相似符号语言：在△ABC与△DEF中，∵ ， ∴△ABC∽△DEF. 例1例2例3教学反思                                                 教学反思                                                        教学反思                                                        教学反思                                                        教学反思