数学必修 第二册4.2.3 对数函数的性质与图像教课课件ppt

这是一份数学必修 第二册4.2.3 对数函数的性质与图像教课课件ppt，共32页。PPT课件主要包含了课前自主学习，描点画图，ylogax，0+∞，-∞0，课堂合作探究，课堂学业达标等内容，欢迎下载使用。
1.思考:已知函数y=2x,那么反过来,x是否为关于y的函数?提示:由于y=2x是单调函数,所以对于任意y∈(0,+∞),都有唯一确定的x与之对应,故x也是关于y的函数,其函数关系式是x=lg2y,此处y∈(0,+∞).2.思考:对数函数中两个变量的取值范围是什么?提示:变量x的取值范围与指数函数中的y的取值范围相同,即(0,+∞).变量y的取值范围与指数函数中的x的取值范围相同,即为R.
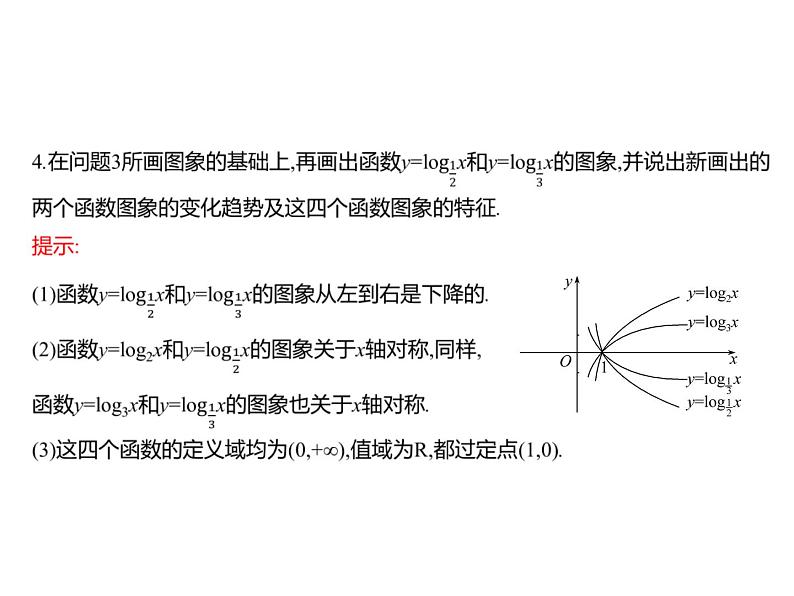
3.在同一坐标系内画出函数y=lg2x和y=lg3x的图象.并说出函数图象从左到右的变化趋势.提示:(1)列表
(2)图象的变化趋势:这两个函数的图象从左到右均是不断上升的.
概念生成1.对数函数的概念一般地,函数_______称为对数函数,其中a是常数,a>0,且a≠1,x是自变量,即函数的定义域是_______.提醒:对数函数的形式是唯一的,自变量x的指数、系数的值均为1.对数函数的底数是大于0且不等于1的常数.对数式的系数也是1.
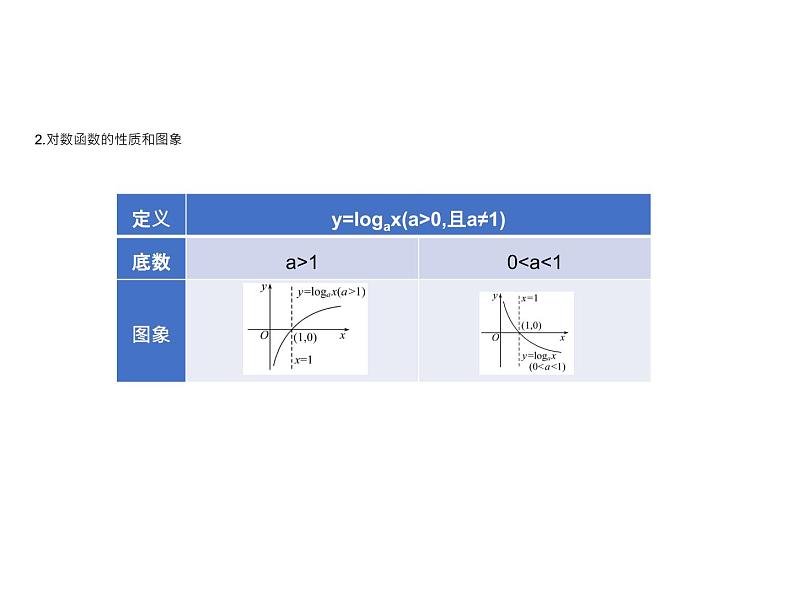
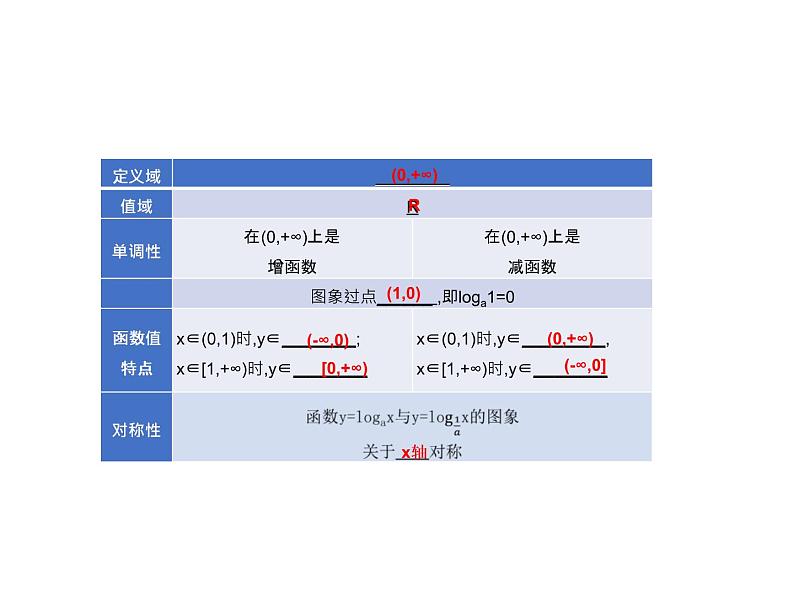
2.对数函数的性质和图象
3.对数函数图象的变化规律结论:左右比较(比较图象与y=1的交点),交点的横坐标越大,对应的对数函数的底数越大.
探究点一　对数函数的概念【典例1】指出下列函数哪些是对数函数:(1)y=2lg3x.(2)y=lg5x.(3)y=lgx2.(4)y=lg2x+1.
【思维导引】观察函数解析式的形式,看是否满足对数函数的定义,然后再下结论.【解析】(1)lg3x的系数是2,不是1,不是对数函数.(2)是对数函数.(3)自变量在底数位置,不是对数函数.(4)对数式lg2x后又加1,不是对数函数.
【类题通法】判断一个函数是否是对数函数的方法(1)看形式:判断一个函数是否是对数函数,关键是看解析式是否符合y=lgax(a>0且a≠1)这一结构形式.(2)明特征:对数函数的解析式具有三个特征:①系数为1;②底数为大于0且不等于1的常数;③对数的真数仅有自变量x.只要有一个特征不具备,则不是对数函数.
2.函数f(x)=lg2(x-1)的零点为(　　)A.4B.3C.2D.1【解析】选C.求解lg2(x-1)=0可得x-1=1⇒x=2.
【类题通法】1.根据对数函数图象判断底数大小的方法作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.2.对数型函数图象恒过定点问题解决此类问题的根据是对任意的a>0且a≠1,都有lga1=0.例如,解答函数y=m+lgaf(x)(a>0且a≠1)的图象恒过定点问题时,只需令f(x)=1求出x,即得定点(x,m).
定向训练1.函数y=3+lga(2x+3)的图象必经过定点的坐标为(　　)A.(-1,3)B.(-1,4)C.(0,3)D.(2,2)【解析】选A.因为当x=-1时,y=3+0=3,所以该函数的图象必经过定点(-1,3).
2.已知等式lg2m=lg3n,m,n∈(0,+∞)成立,那么下列结论:(1)m=n;(2)n