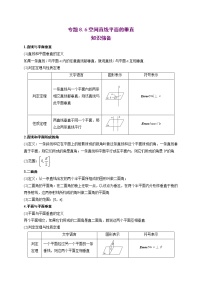
高中8.6 空间直线、平面的垂直优秀同步练习题

这是一份高中8.6 空间直线、平面的垂直优秀同步练习题，文件包含高中数学新教材同步讲义必修第二册86空间直线平面的垂直1精讲教师版含解析docx、高中数学新教材同步讲义必修第二册86空间直线平面的垂直1精讲学生版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

第一，必修课程，由国家根据学生全面发展需要设置，所有学生必须全部修习、全部考试。
第二，选择性必修课程，由国家根据学生个性发展和升学考试需要设置。
第三，选修课程，由学校根据实际情况统筹规划开设，学生自主选择修习。
2、课程类别变化，必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下，对原必修课程学分进行重构，由必修课程学分、选择性必修课程学分组成，适当增加选修课程学分。
3、学时和学分变化，高中生全年假期缩减到11周。
4、授课方式变化，选课制度将全面推开。
5、考试方式变化，高考统考科目由教育部命题，学业水平合格性、等级性考试由各省命题。
8.6 空间直线、平面的垂直(1)(精讲)
思维导图
常见考法
考法一 线面垂直
【例1】(2021·江西景德镇市·景德镇一中)在四棱锥中，，，平面，为的中点，为的中点，．
(1)取中点，证明：平面；
(2)求点到平面的距离.
【举一反三】
1．(2021·陕西省黄陵县中学高一期末)如图所示，为的直径，C为上一点，平面，于E，于F.求证：平面.
2．(2021·宁夏银川市·银川一中高一期末)如图，在三棱锥中，平面ABC，底面ABC是直角三角形，，O是棱的中点，G是的重心，D是PA的中点.
(1)求证：平面；
(2)求证：平面；
3．(2021·陕西咸阳市·高一期末)将棱长为2的正方体沿平面截去一半(如图1所示)得到如图2所示的几何体，点，分别是，的中点.
(Ⅰ)证明：平面；
(Ⅱ)求三棱锥的体积.
考法二 线线垂直
【例2】(2020·全国专题练习)如图，在三棱柱中，侧面为矩形， ，D是的中点，与交于点O，且平面
(1)证明：；
(2)若，求三棱柱的高.
【举一反三】
1．(2021·西安市航天城第一中学高一期末)如图，在三棱柱中，侧棱⊥底面，，分别为棱的中点．
(1)求证：；
(2)若求三棱锥的体积．
2．(2021·广西河池市·高一期末)如图，在三棱柱中，，．
(1)若三棱柱的体积为1，求三棱锥的体积；
(2)证明：．
3．(2021·扶风县法门高中高一期末)如图，三棱锥V—ABC中， VA=VB＝AC=BC=，AB＝，VC=1．
(1)证明： AB⊥VC；
(2)求三棱锥V—ABC的体积．
考法三 面面垂直
【例3】(2021·江西景德镇市·景德镇一中高一期末)如图，四棱锥中，底面是正方形，平面，，为与的交点，为棱上一点.
(1)证明：平面平面；
(2)若平面，求三棱锥的体积.
【举一反三】
1．(2021·陕西宝鸡市·高一期末)如图，在三棱锥中，，，，，为线段的中点，为线段上一点．
(1)求证：平面平面；
(2)当面时，求三棱锥的体积．
2．(2021·全国高一课时练习)在四棱锥中，底面ABCD为矩形，平面PCD，E，F分别为PC，AB的中点求证：
(1)平面平面ABCD；
(2)平面PAD
3．(2021·全国高一课时练习)如图所示，已知在三棱锥中，，M为的中点，D为的中点，且为正三角形．
(Ⅰ)求证：平面；
(Ⅱ)求证：平面平面；
(Ⅲ)若，求三棱锥的体积．
考法四 空间距离
【例4】(2020·全国专题练习)在棱长为的正方体中求出下列距离：
(1)点到面的距离；
(2)线段到面的距离；
(3)点到面的距离；
(4)到平面的距离.
【举一反三】
1．(2020·北京二十中高一期末)如图，正四棱锥的高为，且底面边长也为，则点到平面的距离为( )
A．B．C．D．
2．(2020·全国)已知正四棱柱ABCD- A1B1C1D1中 ，AB=2，CC1= E为CC1的中点，则直线AC1与平面BED的距离为
A．2B．C．D．1
3．(2020·全国高一课时练习)已知是长方体，且，，.
(1)写出点A到平面的距离；
(2)写出直线AB到平面的距离；
(3)写出平面与平面之间的距离.