专题40 代数综合压轴题-2023年中考数学二轮专题提升训练

这是一份专题40 代数综合压轴题-2023年中考数学二轮专题提升训练，共24页。试卷主要包含了配方法的应用，一元二次方程与二次函数的综合，含参二次函数，二次函数与几何综合，绝对值概念的应用等内容，欢迎下载使用。

专题40 代数综合压轴题
类型一 配方法的应用
（2022•南京模拟）
1．利用我们学过的完全平方公式及不等式知识能解决方程或代数式的一些问题，请阅读下列材料：
阅读材料：若，求m、n的值．
解：∵，
∴，
∴，
∴，，
∴，．
根据你的观察，探究下面的问题：
(1)已知，求a、b的值；
(2)已知的三边长a、b、c都是正整数，且满足，求c的值；
(3)若，，试比较A与B的大小关系，并说明理由．
（2022秋•和平区校级期末）
2．已知多项式，．
（1）若，化简；
（2）若的结果中不含有项以及项，求的值．
3．已知，，求的值．
类型二 一元二次方程与二次函数的综合
（2011•东城区二模）
4．已知关于x的一元二次方程，．
(1)若方程有实数根，试确定a，b之间的大小关系；
(2)若，且，求a，b的值；
(3)在（2）的条件下，二次函数的图象与x轴的交点为A、C（点A在点C的左侧），与y轴的交点为B，顶点为D．若点是四边形边上的点，试求的最大值．
（2021秋•沙市区校级期中）
5．已知：关于x的一元二次方程（m为实数）．
(1)若方程有两个不相等的实数根，求m的取值范围；
(2)在（1）的条件下，求证：无论m取何值，抛物线总过x轴上的一个固定点．
类型三 含参二次函数
（2021•邯郸模拟）
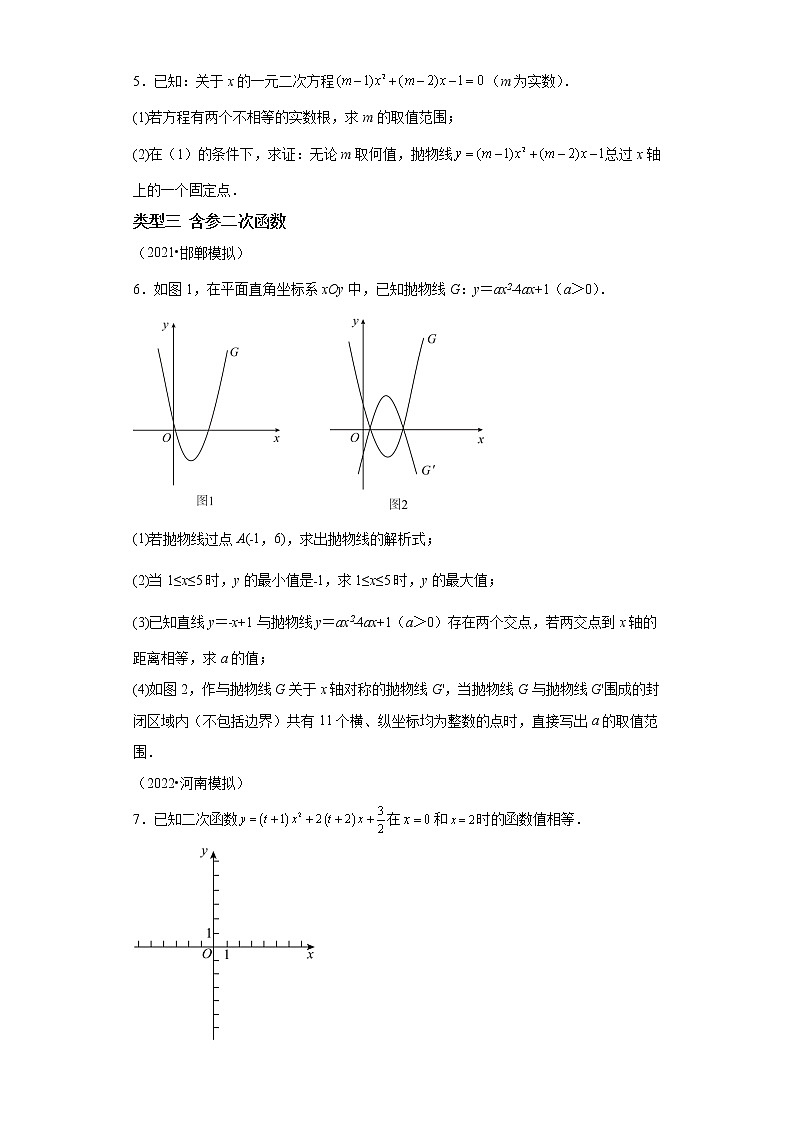
6．如图1，在平面直角坐标系xOy中，已知抛物线G：y＝ax2﹣4ax+1（a＞0）．
　　　
(1)若抛物线过点A(﹣1，6)，求出抛物线的解析式；
(2)当1≤x≤5时，y的最小值是﹣1，求1≤x≤5时，y的最大值；
(3)已知直线y＝﹣x+1与抛物线y＝ax2﹣4ax+1（a＞0）存在两个交点，若两交点到x轴的距离相等，求a的值；
(4)如图2，作与抛物线G关于x轴对称的抛物线G'，当抛物线G与抛物线G'围成的封闭区域内（不包括边界）共有11个横、纵坐标均为整数的点时，直接写出a的取值范围．
（2022•河南模拟）
7．已知二次函数在和时的函数值相等．

（1）求二次函数的解析式；
（2）若一次函数的图象与二次函数的图象都经过点，求和的值；
（3）把二次函数的图象与轴两个交点之间的部分记为图象，把图象向左平移个单位后得到的图象记为，请结合图象回答：当（2）中得到的直线与图象有公共点时，求的取值范围．
8．已知抛物线与x轴有两个不同的交点．
(1)求m的取值范围；
(2)判断点是否在抛物线上；
(3)当时，求抛物线的顶点Q及P点关于抛物线的对称轴对称的点的坐标，并过，Q，P三点，画出抛物线草图．
（2020•西青区二模）
9．已知抛物线C1：y=ax2﹣4ax﹣5（a＞0）．
（1）当a=1时，求抛物线与x轴的交点坐标及对称轴；
（2）①试说明无论a为何值，抛物线C1一定经过两个定点，并求出这两个定点的坐标；
②将抛物线C1沿这两个定点所在直线翻折，得到抛物线C2，直接写出C2的表达式；
（3）若（2）中抛物线C2的顶点到x轴的距离为2，求a的值．
类型四 二次函数与几何综合
（2022•东海县一模）
10．如图，已知抛物线与x轴交于点A、B，与y轴交于点C．

(1)则点A的坐标为_________，点B的坐标为_________，点C的坐标为_________；
(2)设点，（其中）都在抛物线上，若，请证明：；
(3)已知点M是线段上的动点，点N是线段上方抛物线上的动点，若，且与相似，试求此时点N的坐标．
（2021秋•越秀区校级期中）
11．已知抛物线（a为常数）．
（1）求证：无论a取任何实数，此抛物线与x轴总有两个不相同的交点；
（2）抛物线与x轴的两个交点为，抛物线顶点为点D．
①若是直角三角形两条直角边的长，该直角三角形斜边长为4，求a的值；
②点E在抛物线对称轴上，是等腰三角形，求出点E的纵坐标．
类型五 一次函数与二次函数的综合实际应用
（2022•铁西区二模）
12．某商家经销一种绿茶，已知绿茶每千克成本50元，在第一个月的试销时间内发现，销量随销售单价的变化而变化，具体变化规律如下表：
销售单价（元/千克）
…
70
75
80
85
…
x
…
月销售量（千克）
…
100
90
80
_____
…
_____
…

（1）请根据上述关系，完成表格．
（2）用含有x的代数式表示月销售利润；并利用配方法求月销售利润最大值；
（3）在第一个月里，按月销售利润取最大值时的销售单价进行销售后，在第二个月里受物价部门干预，销售单价不得高于90元；且加上其他费用3000元．若商家要想在全部收回投资的基础上使第二个月的利润达到1700元，那么第二个月里应该确定销售单价为多少元?
类型六 绝对值概念的应用
（2021秋•姜堰区期中）
13．【阅读】已知m、n两个数在数轴上对应的点为M、N，其中 ，求M、N两点之间的距离．
小明利用绝对值的概念，结合数轴，进行探索：
解：因为m＞n，所以有以下情况：
情况1：若，，如图①，M、N两点之间的距离；
情况2：若，，如图②，M、N两点之间的距离；
情况3：若，，如图③，M、N两点之间的距离．
由此小明得出结论：若m、n两个数在数轴上对应的点为M、N，其中，则M、N两点之间的距离．
【应用】
在数轴上，点A表示的数为a，点B表示的数为b，点C对应的数为c．

(1)若 ，，则a＝　　．
(2)若，，点C到点A的距离是点C到点B距离的倍．
①当时，求c的值；
②对于任意一个n的值，满足条件的点C的个数始终有2个，请直接写出n取值范围 　　．
(3)若，且a、b为整数，当的值最大时，求A、B两点之间的距离．



参考答案：
1．(1)，
(2)
(3)，详见解析

【分析】（1）将多项式拆分为完全平方展开式的形式，最后配凑为完全平方，再根据平方的性质求解．
（2）先配凑完全平方公式求出a，b值，再根据三角形三边关系求出第三边．
（3）利用作差法比较大小，配凑完全平方公式并根据平方的性质判断．
【详解】（1）解：∵，
∴，
∴，
∴，，
∴，．
（2）解：∵，
∴
∴，
∴，，
解得，，
∵a、b、c是的三边长，
∴，
∵c是正整数，
∴；
（3）解：，理由如下：
∵，，
∴


，
∵，
∴，
∴．
【点睛】本题考查完全平方公式的应用，解题的关键是合理配凑完全平方公式．
2．（1），（2）-5
【分析】（1）根据非负数的性质求出m、n，再计算A-B即可；
（2）先计算，再根据不含项以及项，得出m、n的值，代入即可．
【详解】解：（1）∵，
∴，
解得，，
∴，，
，
=，
=．
（2），
=，
∵结果中不含有项以及项，
∴，，
解得，，
把代入，
．
【点睛】本题考查了非负数的性质和整式的加减以及代数式求值，解题关键是能够根据非负数的性质或多项式不含某一项确定字母系数的值，并能熟练应用整式加减的法则进行计算．
3．0
【分析】由，得出，进一步代入整理得出a、b、c的数值得出答案即可；
【详解】解：，
，
，
，
，
，
解得：，，
，
．
【点睛】此题考查因式分解的实际运用，非负数的性质，掌握完全平方公式是解决问题的关键．
4．(1)；
(2)；
(3)最大z的值等于．

【分析】（1）根据方程有实数根可以得到其根的判别式为非负数，然后再根据作出判断即可；
（2）利用a与b的比值分别设出a和b，利用根与系数的关系用设出的未知数表示出方程的两个解，代入中求得a与b的值即可；
（3）将上题中求得的a与b的值代入到函数中确定函数的解析式，然后求得与x轴的交点坐标，与y轴的交点坐标和顶点坐标，据此可以求出的最大值．
【详解】（1）解：∵关于x的一元二次方程有实数根，
∴，
有，
．
∵，
∴．
∴；
（2）解：∵，
∴设．
∴原方程为，
解得或．
当时，由得．
当时，由得（不合题意，舍去）．
∴；
（3）解：当时，
二次函数解析式为，
令，则，
解得或．
二次函数与x轴的交点坐标分别为、，
与y轴交点坐标为，顶点坐标D为．
设，则．
画出函数和的图象，若直线平行移动时，如图

可以发现当直线经过点C时符合题意，此时最大z的值等于．
【点睛】本题考查了函数综合知识，函数综合题是初中数学中覆盖面最广、综合性最强的题型．近几年的中考压轴题多以函数综合题的形式出现．解决函数综合题的过程就是转化思想、数形结合思想、分类讨论思想、方程思想的应用过程．
5．(1)，或
(2)证明见解析

【分析】（1）根据与0的关系即可判断出关于x的一元二次方程（m为实数）的解的情况；
（2）函数解析式变形后，根据题意确定出x的值进而得出定点即可．
【详解】（1）根据题意，得，即，
解得或①，
又∵，
∴②，
由①②，得，或；
（2），
∵无论m取何值，抛物线总过x轴上的一个固定点，
∴，即，
解得：或，
当时，，定点为；
当时，，定点为，
则无论m取何值，抛物线总过x轴上的一个固定点．
【点睛】此题考查了抛物线与x轴的交点，以及根的判别式，在解一元二次方程的根时，利用根的判别式与0的关系来判断该方程的根的情况．
6．(1)抛物线的解析式为y＝x2﹣4x+1
(2)y的最大值为
(3)
(4)

【分析】（1）把A（﹣1，6）代入y＝ax2﹣4ax+1，即可求解；
（2）先求出抛物线的对称轴为直线x＝2，可得抛物线的顶点的纵坐标就是y的最小值﹣1，从而得到抛物线的解析式为y＝x2﹣2x+1，然后根据二次函数的增减性，即可求解；
（3）根据题意得直线y＝﹣x+1及抛物线y＝ax2﹣4ax+1与y轴的交点都是（0，1），从而得到直线y＝﹣x+1与抛物线y＝ax2﹣4ax+1的两个交点到x轴的距离都是1，进而得到另一个交点的纵坐标为﹣1，再代入直线y＝﹣x+1可得另一个交点的坐标，即可求解；
（4）根据题意可得抛物线G与抛物线G′围成的封闭区域是以x轴为对称轴的轴对称图形，从而得到x轴的下方和上方各有四个这样的点，且两两关于x轴对称．进而得到对于抛物线G，当x＝1时，y＝﹣3a+1；当x＝2时，y＝﹣4a+1，可得到，解出即可求解．
【详解】（1）解：把A（﹣1，6）代入y＝ax2﹣4ax+1，得a+4a+1＝6，解得a＝1，
∴抛物线的解析式为y＝x2﹣4x+1．
（2）解：∵y＝ax2﹣4ax+1＝a（x﹣2）2﹣4a+1，
∴抛物线的对称轴为直线x＝2，
∵抛物线的顶点的横坐标在1≤x≤5的范围内，
∴抛物线的顶点的纵坐标就是y的最小值﹣1，
∴﹣4a+1＝﹣1，
解得a＝，
∴抛物线的解析式为y＝x2﹣2x+1，
当1≤x≤2时，y随x的增大而减小，当x＝1时，y最大＝﹣2+1＝﹣；
当2＜x≤5时，y随x的增大而增大，当x＝5时，y最大＝﹣2×5+1＝，
∵﹣＜，
∴y的最大值为；
（3）解：根据题意得：直线y＝﹣x+1及抛物线y＝ax2﹣4ax+1与y轴的交点都是（0，1），
∴直线y＝﹣x+1与抛物线y＝ax2﹣4ax+1的两个交点到x轴的距离都是1，且其中一个交点坐标为（0，1），
∴另一个交点的纵坐标为﹣1，
当y＝﹣1时，由﹣1＝﹣x+1，得x＝2，
∴另一交点坐标为（2，﹣1），
把（2，﹣1）代入y＝ax2﹣4ax+1得4a﹣8a+1＝﹣1，解得．
（4）解：由题意可知，抛物线G与抛物线G′围成的封闭区域是以x轴为对称轴的轴对称图形，
∴该区域内x轴上有三个横、纵坐标均为整数的点，x轴的下方和上方各有四个这样的点，且两两关于x轴对称．
如图，对于抛物线G，当x＝1时，y＝﹣3a+1；当x＝2时，y＝﹣4a+1，
由题意，得，
解得＜a≤1，
∴a的取值范围是＜a≤1．

【点睛】本题主要考查了二次函数的图象和性质，二次函数与一次函数的交点问题，熟练掌握二次函数的图象和性质，二次函数与一次函数的交点问题，并利用数形结合思想解答是解题的关键．
7．（1）；（2），；（3）
【分析】（1）根据已知条件知，该函数的对称轴方程为，则，据此易求的值，把的值代入函数解析式即可；根据图象与坐标轴的交点坐标，顶点坐标画出图象；
（2）把点的坐标代入二次函数解析式，利用方程可以求得的值；然后把点的坐标代入一次函数解析式，也是利用方程来求的值；
（3）求出点、间的部分图象的解析式是，得出抛物线平移后得出的图象的解析式是，，直线的解析式是，若两图象有一个交点时，得出方程有两个相等的实数解，求出判别式△，求出的的值与已知相矛盾，得出平移后的直线与抛物线有两个公共点，设两个临界的交点为，，代入直线的解析式，求出的值，即可得出答案．
【详解】解：（1）二次函数在和时的函数值相等，
对称轴，解得，，
则二次函数的解析式为：，
即或，
（2）二次函数的象经过点，
．
又一次函数的图象经过点，
，即，
解得，．
综上所述，和的值分别是、4；
（3）解：由题意可知，图象的解析式是，，
则抛物线平移后得出的图象的解析式是，，
此时直线平的解析式是，
如果直线与平移后的二次函数相切，
则方程有两个相等的实数解，
即有两个相等的实数解，
判别式△，
即，
与已知相矛盾，
平移后的直线与平移后的抛物线不相切，
结合图象可知，如果平移后的直线与抛物线有公共点，
则两个临界的交点为，，
则，
，
，
，
即的取值范围是：．

【点睛】本题考查了待定系数法求二次函数的解析式，二次函数的图象以及二次函数图象上点的坐标特征．求得二次函数的解析式时，利用了二次函数图象的对称性质．
8．(1)或
(2)在抛物线上
(3)见解析

【分析】（1）与x轴有两个不同的交点即令，得到的一元二次方程的判别式，据此即可得到不等式求解；
（2）把点代入函数解析式判断是否成立即可；
（3）首先求得函数解析式，即可求得定点坐标以及对称轴，则的坐标即可求得，然后根据三点即可作出函数图象．
【详解】（1）∵抛物线与x轴有两个不同的交点，
∴，
解得：或；
（2）当时，，则点在抛物线上；
（3）当时，抛物线是：，
，
把代入 得，则Q的坐标是；
对称轴是直线，则P'的坐标是．
则函数的图象是：

【点睛】本题考查了二次函数图象与x轴的公共点的个数的判定方法，如果，则抛物线与x轴有两个不同的交点；如果，与x轴有一个交点；如果，与x轴无交点．
9．（1）（﹣1，0）或（5，0）；对称轴为x=2；（2）①（0，﹣5），（4，﹣5）②y=﹣ax2+4ax﹣5（3）a=或
【分析】（1）将a=1代入解析式，即可求得抛物线与x轴交点；
（2）①化简抛物线解析式，即可求得两个点定点的横坐标，即可解题；
②根据抛物线翻折理论即可解题；
（3）根据（2）中抛物线C2解析式，分类讨论y=2或﹣2，即可解题
【详解】（1）当a=1时，抛物线解析式为y=x2﹣4x﹣5=（x﹣2）2﹣9，
∴对称轴为x=2；
∴当y=0时，x﹣2=3或﹣3，即x=﹣1或5；
∴抛物线与x轴的交点坐标为（﹣1，0）或（5，0）；
（2）①抛物线C1解析式为：y=ax2﹣4ax﹣5，
整理得：y=ax（x﹣4）﹣5；
∵当ax（x﹣4）=0时，y恒定为﹣5；
∴抛物线C1一定经过两个定点（0，﹣5），（4，﹣5）；
②这两个点连线为y=﹣5；
将抛物线C1沿y=﹣5翻折，得到抛物线C2，开口方向变了，但是对称轴没变；
∴抛物线C2解析式为：y=﹣ax2+4ax﹣5，
（3）抛物线C2的顶点到x轴的距离为2，
则x=2时，y=2或者﹣2；
当y=2时，2=﹣4a+8a﹣5，解得，a=；
当y=﹣2时，﹣2=﹣4a+8a﹣5，解得，a=；
∴a=或；
考点：1、抛物线与x轴的交点；2、二次函数图象与几何变换
10．(1)（1，0），（4，0），(0，2)；
(2)证明见解析；
(3)点N的坐标为（，）或（3，2）．

【分析】（1）分别令和，即可求出点A、B、C的坐标；
（2）由题意，结合，利用作差法即可求出，即可得到结论成立；
（3）过点N作NG⊥y轴于点G，过点M作MH⊥GN于点H，先求出直线BC的函数表达式为，然后分成两种情况进行分析：①CN：MN=1：2或②CN：MN=2：1，分别求出答案即可．
【详解】（1）解：∵与x轴交于点A、B，与y轴交于点C．
令，则；
∴点C的坐标为（0，2）；
令，则，
解得：或；
∴点A为（，0），点B为（4，0）；
故答案为：（，0），（，0），（0，2）；
（2）解：∵，由题意得



=．
∵，
∴．
∴．
（3）解：过点N作NG⊥y轴于点G，过点M作MH⊥GN于点H．

由点B、C的坐标分别为（4，0），(0，2)，
易得直线BC的函数表达式为．
设点N的坐标为（n，），则GN=n，GC=．
当∠CNM=90°时，易得△CNG∽△NMH．
①△CMN中CN：MN=1：2，
则易得NH=2()=，HM=2 n．
∴点M的坐标为（，）．
该点在直线BC上，则有=．
解得：（舍去）， ．
此时可得点N坐标为（，）．
②若△CMN中CN：MN=2：1，
则易得NH=()=，HM=n．
所以点M的坐标为（，）．
可得=（）+2．
解得：（舍去）， ．
此时可得点N坐标为（3，2）．
综上所述，点N的坐标为（，）或（3，2）．
【点睛】本题考查了二次函数的图象和性质，相似三角形的判定和性质，利用作差法比较大小，解题的关键是熟练掌握题意，正确的作出辅助线，运用分类讨论、数形结合的思想进行解题．
11．（1）证明见解析；（2）①的值为：； ②的纵坐标为：或或或
【分析】（1）先证明从而可得结论；
（2）①由题意得：是方程的两个根，可得 由是直角三角形两条直角边的长， 即 再消去建立关于的方程，解方程并检验即可；②先求解抛物线的顶点坐标，抛物线与轴的交点坐标，再分三种情况讨论：当时，当时，当时，从而可得答案.
【详解】解：（1） 抛物线，


所以无论a取任何实数，此抛物线与x轴总有两个不相同的交点；
（2）①由题意得：是方程的两个根，

又是直角三角形两条直角边的长，该直角三角形斜边长为4，
即

整理得：
解得：
经检验： 所以舍去，取
所以的值为：
② 抛物线，
抛物线的顶点D坐标为：
令 则
解得：

点E在抛物线对称轴上，是等腰三角形，
当时，如图，记对称轴与轴的交点为N，

即的纵坐标为
当时，设 如图，


解得：
所以的纵坐标为：或
当时，

解得：
所以的纵坐标为：，
综上：的纵坐标为：或或或
【点睛】本题考查的是抛物线与轴的交点问题，一元二次方程根与系数的关系，等腰三角形的性质，熟练的运用抛物线与图形的性质解决抛物线与等腰三角形问题，清晰的分类讨论是解本题的关键.
12．（1）70，；（2）月销售利润为﹣2x2+340x﹣12000，月销售利润最大值为2450；（3）75
【分析】（1）利用表格中数据可知销售单价每增加5元，月销售量下降10千克，由此可求得答案；
（2）利用销售利润＝单价×销售量列出函数关系式，利用配方法可求最值；
（3）首先根据第一个月的利润，得出要想在全部收回投资的基础上使第二个月的利润达到1700元，即第二个月必须获得2250元的利润，把函数值2250代入，解一元二次方程即可．
【详解】解：（1）由题意可知，销售单价每增加5元，月销售量下降10千克，
，



故答案为：70，；
（2）设月销售利润为y，
y＝（x﹣50）•（﹣2x+240）
＝﹣2x2+340x﹣12000，
＝﹣2(x2﹣170x)﹣12000，
＝﹣2(x2﹣170x+7225﹣7225)﹣12000，
＝﹣2（x﹣85）2+14450﹣12000，
＝﹣2（x﹣85）2+2450，
故当x＝85时，y的值最大为2450；
答：月销售利润为﹣2x2+340x﹣12000，月销售利润最大值为2450；
（3）故第1个月还有3000﹣2450＝550元的投资成本没有收回，
则要想在全部收回投资的基础上使第二个月的利润达到1700元，即y＝2250才可以，
可得方程﹣2（x﹣85）2+2450＝2250，
解这个方程，得x1＝75，x2＝95；
根据题意，x2＝95不合题意应舍去．
答：当销售单价为每千克75元时，可获得销售利润2250元，即在全部收回投资的基础上使第二个月的利润达到1700元．
【点睛】此题考查了待定系数法求一次函数解析式以及二次函数的最值以及二次函数与一元二次方程的关系等知识，注意题目中细节描述得出要想在全部收回投资的基础上使第二个月的利润达到1700元，即y＝2250进而求出是解题关键．
13．(1)3或
(2)① 或；②且
(3)

【分析】（1）分两种情况讨论，即点A在点B的左侧，点A在点B的右侧；
（2）①分两种情况讨论，即点C在线段之间，点C在点A的左侧；②分三种情况讨论，即点C在点A的左侧，点C在线段之间，点C在点B的右侧；
（3）根据，的值最大，a，b两个数一定都是负数，又因为a、b为整数，所以a，b的值就确定了，即可求出．
【详解】（1）解：分两种情况：
当点A在点B的右侧，即 时，
∵，
∴，，
当点A在点B的左侧，即时，
∵，
∴，；
（2）解：①分两种情况：
当点C在线段之间时， ，即，，
当点C在点A的左侧时，，即，，
所以，或；
②分三种情况：
当点C在点A的左侧时， ，
当点C在点B的右侧时；，
当点C在线段AB之间时，或，
又因为点C的个数始终有两个，n≠1，
所以 且；
（3）解：∵，的值最大，
∴ ，
因为a、b为整数，
所以，或，，
所以．
【点睛】本题考查了两点间的距离，数轴，绝对值的意义，在未画图类问题中，正确画图是解决问题的关键，同时本题渗透了分类讨论的思想．