数学八年级上册16．2 最简二次根式和同类二次根式优质ppt课件

这是一份数学八年级上册16．2 最简二次根式和同类二次根式优质ppt课件，文件包含沪教版数学八上162《最简二次根式和同类二次根式1》课件ppt、沪教版数学八上162《最简二次根式和同类二次根式1》教案doc等2份课件配套教学资源，其中PPT共19页， 欢迎下载使用。
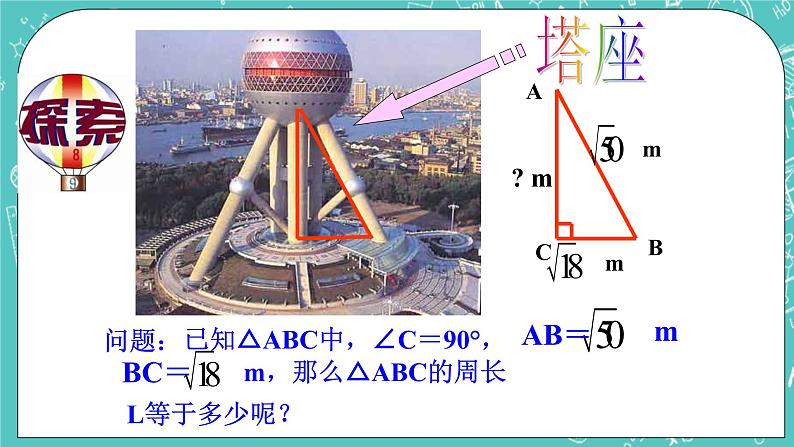
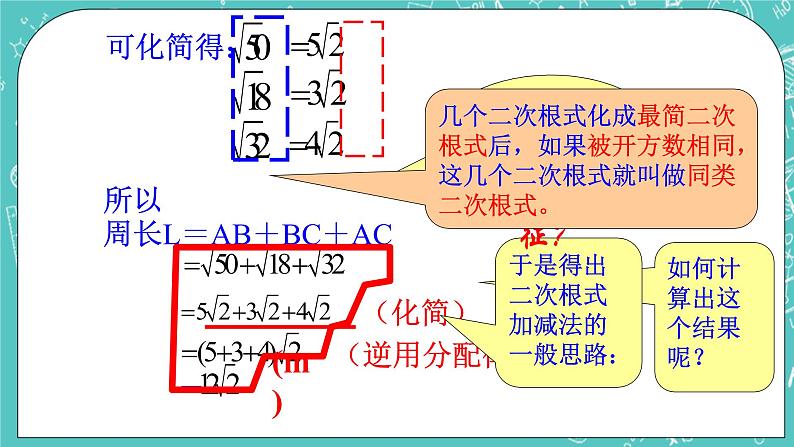
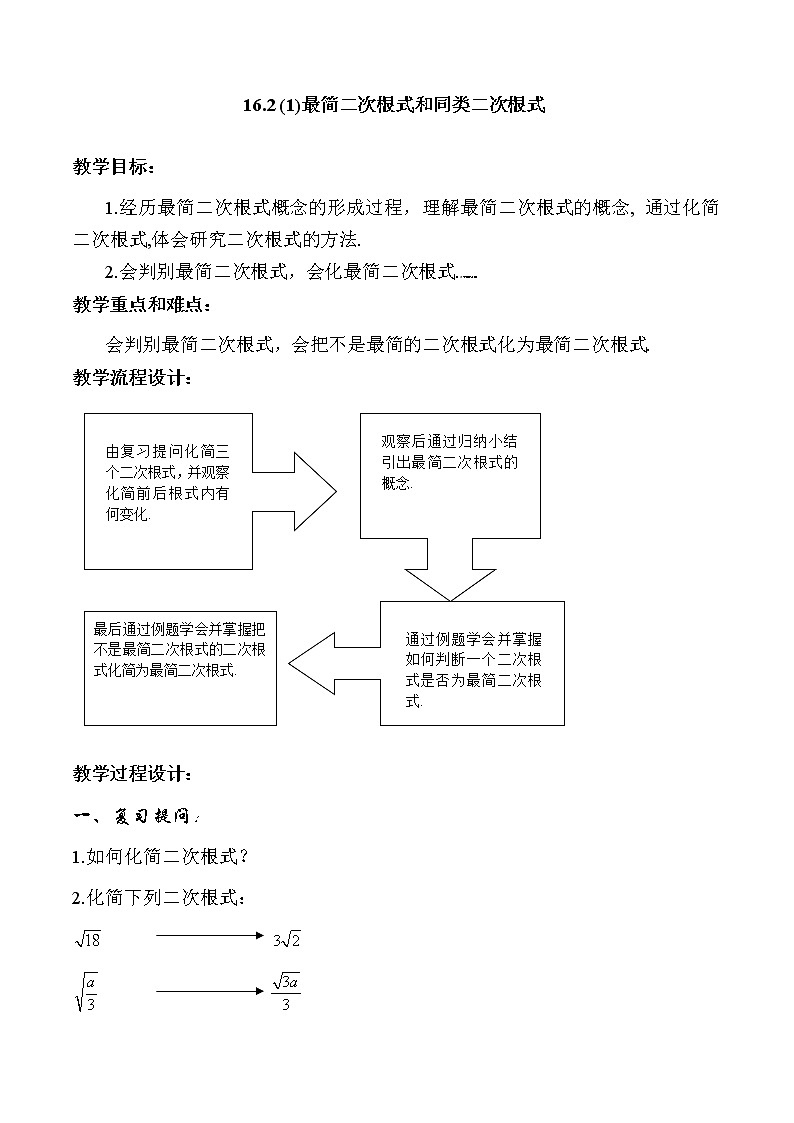
21世纪教育网21世纪教育网16.2 (1)最简二次根式和同类二次根式        教学目标：1.经历最简二次根式概念的形成过程，理解最简二次根式的概念, 通过化简二次根式,体会研究二次根式的方法.2.会判别最简二次根式，会化最简二次根式.21世纪教育网教学重点和难点：会判别最简二次根式，会把不是最简的二次根式化为最简二次根式.教学流程设计：教学过程设计：一、复习提问： 1.如何化简二次根式？2.化简下列二次根式：                                                 二、学习新课：1、观察思考：观察每组两个二次根式里的被开方数前后发生了什么变化,化简后的被开方数是由那些共同的特征.师生共同讨论总结：[来源:21世纪教育网]1）          被开方数中各因式的指数都为1；2）            被开方数不含分母.21世纪教育网师生共同总结：同时符合上述两个条件的二次根式，叫做最简二次根式.举例说明：如、、等都是最简二次根式.21世纪教育网2、例题分析：例1：判断下列二次根式是不是最简二次根式：1）2）3）4）例2：将下列二次根式化成最简二次根式：1）2）3）三、课堂小结：（1）掌握判断最简二次根式的依据：二次根式里被开方数中各因式的指数都为1且被开方数不含分母.（2）化简二次根式时，要特别注意判断根号内字母的取值范围，从而正确化简.四、作业布置：[来源:21世纪教育网]练习册习题16.2(1) 教学设计说明：21世纪教育网1．通过观察三个二次根式的化简结果，顺利引出“最简二次根式”的概念，并通过举例学会判断一个二次根式是否为最简二次根式.2．本节课的教学设计，力求体现出在教师引导下，师生共同讨论、分析、归纳，掌握化成最简二次根式的一般步骤，并通过课堂练习让学生在课堂上达到巩固所学知识的目的．21世纪教育网教学反思：在化简二次根式时，如果要将被开方数中某个完全平方式的因式用它的正的平方根（即算术平方根）代替后移到根式外，那么这个正的平方根（即算术平方根）必须是“非负”的.因此，要根据二次根式有意义以及已给定的条件，判断字母或因式的取值范围.