





沪教版 (五四制)八年级上册19.9 勾股定理优质课课件ppt
展开19.9(1)勾股定理(1)
教学目标
1、理解用面积割补方法证明勾股定理的思路;21世纪教育网
2、感受人类文明的力量,了解中国古代在勾股定理方面的成就,知道勾股定理在人类重大科技发现中的地位; [来源:21世纪教育网]
3、初步掌握勾股定理,并能进行简单运用.
教学重点及难点
面积割补法证明勾股定理
教学用具准备[来源:21世纪教育网]
黑板、粉笔、学生准备课堂练习本
教学流程设计
教学过程设计
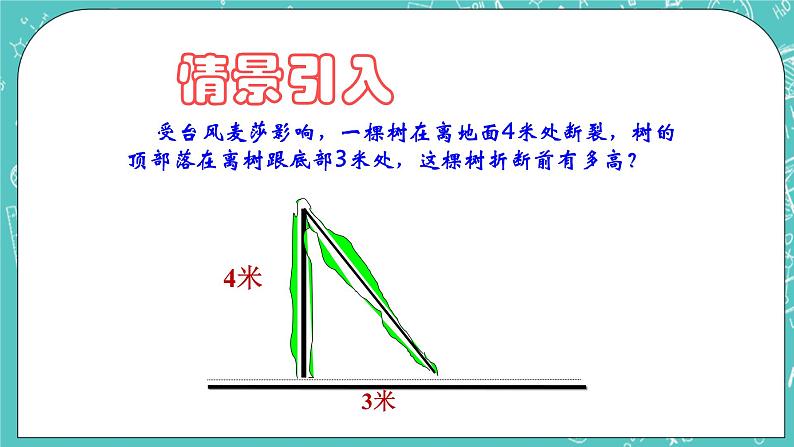
一、引入定理一
任意一个直角三角形总有一边最长:斜边.(学生回答)
直角三角形中,两锐角互余.
二、勾股定理
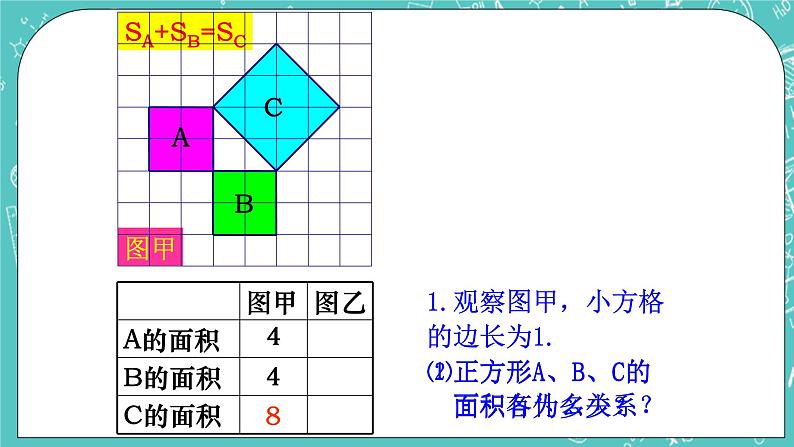
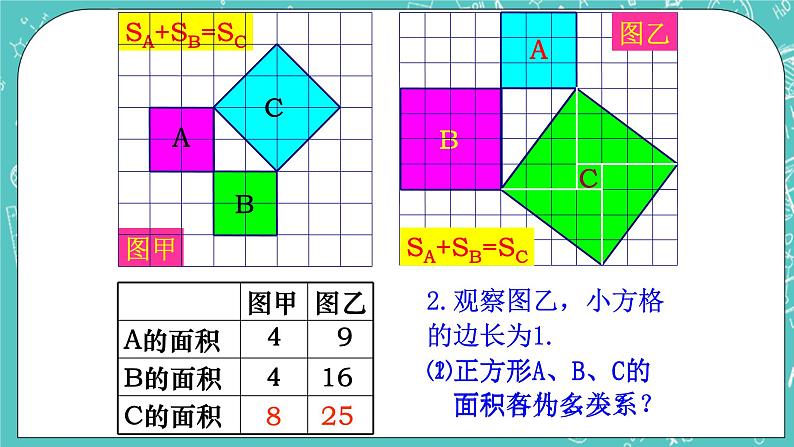
教师:想想七年级时怎么得到的?(提示:用边长为1的正方形进行拼接得到)
课件演示
教师:当边长为m时可发现三角形斜边长为m
得到特殊情况下:在等腰直角三角形中,两条直角边的平方和等于斜边的平方.
教师:等腰直角三角形的边能有数量关系,这个结论很好,这就意味着以后等腰直角三角形中的几何问题可以代数化了,不过这个结论的条件还比较苛刻,如果能减少条件那就更好了,比如说:在直角三角形中.
换句话说,我想要看看“在直角三角形中,两条直角边的平方和等于斜边的平方.”这个命题是否真命题.
这里有一个前人的证法,跟我们前面的证明方法类似.
这种证明方法称作面积割补法.由此发现我们前面的假设成立.其实这是一个很有名的定理.
勾股定理:在直角三角形中,两条直角边的平方和等于斜边的平方.
老师:中国古代称直角三角形的较短直角边为勾,较长直角边为股,斜边为弦,因此称作勾股定理.中国古人对于勾股定理的研究在公园前一千多年就开始了,她还有一个名字叫商高定理,《周髀算经》中记载了商高与周公的一段对话谈到了勾股定理,因此称为商高定理;在西方勾股定理还被称作“毕达哥拉斯定理”或“百牛定理”因为古希腊有一个叫毕达哥拉斯的数学家在公园前五百多年发现了这一定理,当时他的学派宰牛百头,广设盛宴,以示庆贺,但她们却并不知道在这之前五百年中国人就已经发现了.
老师:能不能把勾股定理的文字语言转化成数学语言?
学生:在Rt⊿ABC中,∠C=90°,a2+b2=c2
对这个等式可以变形为:
(后两个由学生回答)
二、练习[来源:21世纪教育网]
1、在Rt⊿ABC中,∠C=90°[来源:21世纪教育网]
(1)已知a=3,b=4, 求c
(2)已知a=8,c=10,求b
(3)已知a=3/2,b=2求c
(4)已知a=5,b=12,求c21世纪教育网
(5)已知c=25,b=24,求a
(6)已知a=1,c=2, 求b
(7)已知a=b=1, 求c
(8)已知a=b=, 求c
2、在Rt⊿BCA中,∠A=90°
(1)已知b=4,c=5, 求a=____
(2)已知a=13,b=5, 求c=____
3、在等腰Rt⊿ABC中,∠C=90°,c=4,求a,b
三、简单应用
求边长为1的等边三角形的面积.
四、课堂小结
这节课我们主要学习了两个定理,都是关于直角三角形的三边之间关系.一个是关于直角三角形的三边的长短关系的,这个定理的具体内容是?还有一个是三边的数量关系,内容是?这个定理称为?
(时间允许的话可以介绍几种著名的勾股定理的证明方法)
教学设计说明
勾股定理在数学中占有极其重要的地位,中国古人对勾股定理的研究也很值得后人骄傲,此课很便于对于民族精神的渗透.虽然在教学目标中民族精神教育的部分占了很大比列,但课堂上我花在这方面的时间很短,不超过2分钟,并非对于这一内容不重视,而是希望能做到润物细无声,不想过份做作.
勾股定理的证明引导学生进行证明很有难度,几乎不可能,所以我选择直接拿出证明方法,只是要求学生理解.
在课的最后特别选择了几种中国古人对于勾股定理的证明方法,扩充面积割补法证明勾股定理的同时也显示了中国人的智慧。
初中数学沪教版 (五四制)八年级上册19.9 勾股定理优质ppt课件: 这是一份初中数学沪教版 (五四制)八年级上册19.9 勾股定理优质ppt课件,文件包含沪教版数学八上199《勾股定理2》课件ppt、沪教版数学八上199《勾股定理2》教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
沪教版 (五四制)八年级上册19.9 勾股定理获奖ppt课件: 这是一份沪教版 (五四制)八年级上册19.9 勾股定理获奖ppt课件,文件包含沪教版数学八上199《勾股定理2》课件ppt、沪教版数学八上199《勾股定理2》教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
2021学年19.9 勾股定理完整版课件ppt: 这是一份2021学年19.9 勾股定理完整版课件ppt