初中数学沪科版九年级上册21.1 二次函数公开课课件ppt

这是一份初中数学沪科版九年级上册21.1 二次函数公开课课件ppt，共20页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，一条直线，单调性，a20等内容，欢迎下载使用。

1.理解二次函数y＝ax2的图象2.掌握二次函数y＝ax2 的性质（重点）
问题1：用描点法画函数图象的一般步骤是什么？
问题2：我们学过的一次函数的图象是什么图形？
那么，二次函数的图象会是什么样的图形呢？这节课我们来学习最简单的二次函数y=ax2的图象.
①列表；②描点；③连线
一次函数的图象是一条直线，二次函数的图象是什么形状呢？它又有什么性质？
知识点1 二次函数y=ax2的图像
例1 画出二次函数 y = x2 的图象.
1.列表 在y = x2中，自变量x可以是任意实数，列表表示出几组对应值：
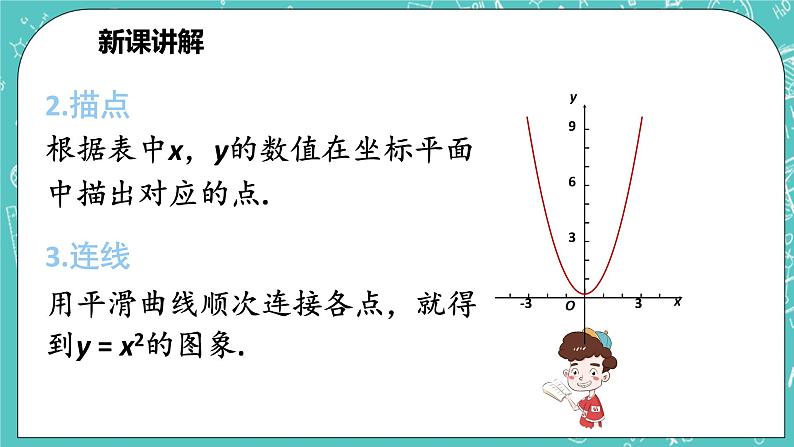
2.描点 根据表中x，y的数值在坐标平面中描出对应的点.
3.连线 用平滑曲线顺次连接各点，就得到y = x2的图象.
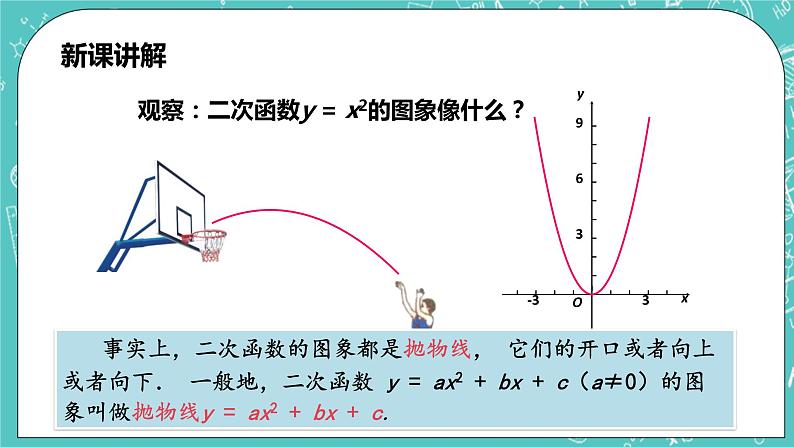
观察：二次函数y = x2的图象像什么？
事实上，二次函数的图象都是抛物线， 它们的开口或者向上或者向下． 一般地，二次函数 y = ax2 + bx + c（a≠0）的图象叫做抛物线y = ax2 + bx + c.
抛物线与对称轴的交点叫做抛物线的顶点。
这条抛物线关于y轴对称，y轴就是它的对称轴.
实际上，每条抛物线都有对称轴，抛物线与对称轴的交点叫做抛物线的顶点.顶点是抛物线的最低点或最高点．
函数y = x2的图象开口______.
1.二次函数的图象都是抛物线.
2.抛物线y=ax2的图象性质:
（2）当a>0时，抛物线的开口向上，顶点是抛物线的最低点;
当a<0时，抛物线的开口向下，顶点是抛物线的最高点;
|a|越大，抛物线的开口越小.
（1）抛物线y=ax2的对称轴是y轴，顶点是原点.
对于抛物线y＝－3x2，下列说法正确的是(　　) A．开口向上，对称轴是x轴 B．开口向下，对称轴是x轴 C．开口向上，对称轴是y轴 D．开口向下，对称轴是y轴
关于二次函数y＝3x2的图象，下列说法错误的是(　　) A．它是一条抛物线 B．它的开口向上，且关于y轴对称 C．它的顶点是抛物线的最高点 D．它与y＝－3x2的图象关于x轴对称
知识点2 二次函数y = ax2的性质
1．二次函数y＝ax2(a≠0)的图象是抛物线，它的顶点是原点，对称轴是y轴．2．二次函数y＝ax2(a≠0)的图象与性质：
导引：根据二次函数y＝ax2(a≠0)的性质直接作答．
已知函数y＝－ x2，不画图象，回答下列各题． (1)开口方向：______； (2)对称轴：_____； (3)顶点坐标：______； (4)当x＞0时，y随x的增大而______； (5)当x____时，y＝0； (6)当x____时，函数值y最____，是___．
在解答函数性质的问题中，即使问题没有要求画函数图象，也应考虑在演算纸上画出函数图象的草图，结合函数图象用数形结合的方法来求解，这样能直观地得到函数的性质．
1.函数y = 2x2的图象的开口_______，对称轴是_______，顶点是________ .
|a|越大，开口越小.
（1）其中开口向上的是________（填序号）；（2）其中开口向下且开口最大的是______（填序号）；（3）有最高点的是_______（填序号）.
2. 已知下列二次函数①y=-x2；②y= x2；③y=15x2；④y =-4x2；⑤y = 4x2.