沪科版九年级上册第21章 二次函数与反比例函数21.1 二次函数完美版课件ppt

这是一份沪科版九年级上册第21章 二次函数与反比例函数21.1 二次函数完美版课件ppt，共26页。PPT课件主要包含了复习导入，y-x2等内容，欢迎下载使用。

1、二次函数的一般形式是怎样的？
y=ax²+bx+c(a,b,c是常数,a≠ 0)
2、下列函数中，哪些是二次函数？
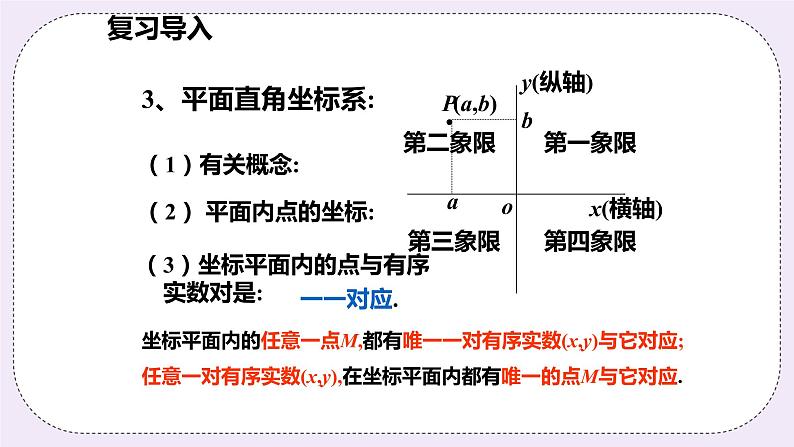
3、平面直角坐标系:（1）有关概念:
（2） 平面内点的坐标:
（3）坐标平面内的点与有序 实数对是:
坐标平面内的任意一点M,都有唯一一对有序实数(x,y)与它对应;任意一对有序实数(x,y),在坐标平面内都有唯一的点M与它对应.
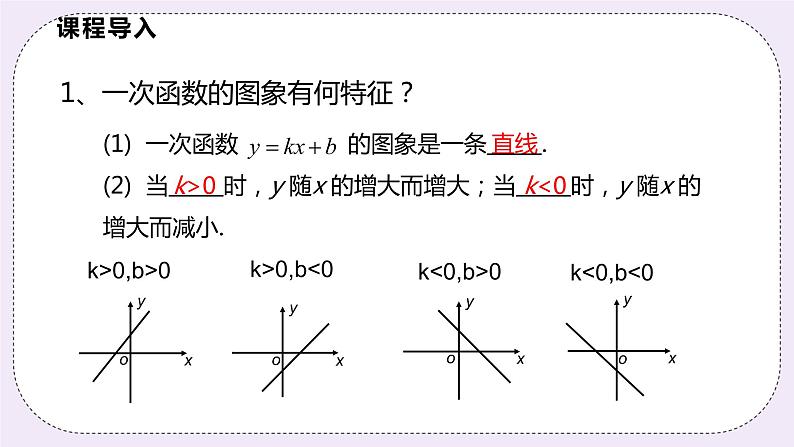
1、一次函数的图象有何特征？
2、二次函数的图象是如何画出来的呢？有何特征
3、画一次函数图象的基本步骤是：
你能通过这种方法画出二次函数的图象吗？
、 、 .
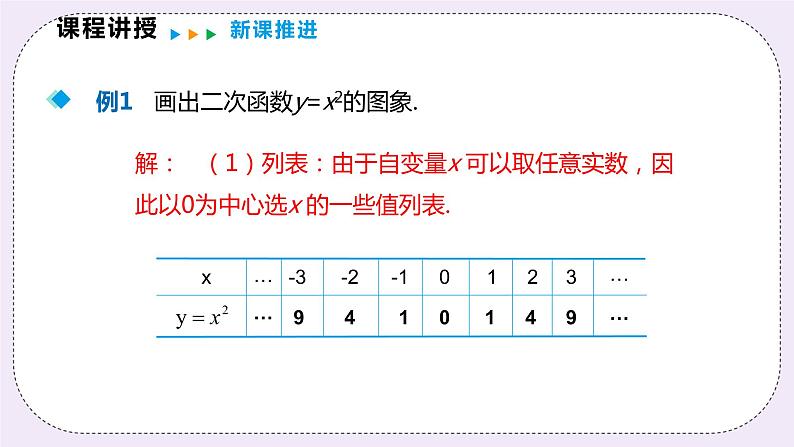
例1 画出二次函数y=x2的图象.
解： （1）列表：由于自变量x 可以取任意实数，因此以0为中心选x 的一些值列表.
(2) 做图象时注意两个象限内画出的曲线是对称的;
(3) 顶点处不能画出尖形,而应平滑;
(1) 画图时图象应该越过端点,表示向上或向下无限延伸；
(4)" 顺序”是指自变量从小到大的顺序（或从左到右）.
①函数y = x2的图象开口______；
抛物线与对称轴的交点叫做抛物线的顶点.
这条抛物线关于y轴对称，y轴就是它的对称轴.
顶点坐标是________.顶点是图象的最____点.
③有最低点，没有最高点.
实际上，每条抛物线都有对称轴，抛物线与对称轴的交点叫做抛物线的顶点.顶点是抛物线的最低点或最高点．
当x<0 (在对称轴的左侧)时，y 随着x 的增大而减小.
当x>0 (在对称轴的右侧)时，y 随着x 的增大而增大.
观察y=x2图象，总结图象特征：
(4) 最值（最大或最小值）:
当x=0时,y有最小值为0
在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大
例2 在同一平面直角坐标系中，画出函数 的图象．
思考：函数 的图象与函数 的图象相比，有什么共同点和不同点？
不同点：a 要越大，抛物线的开口越小
相同点：开口都向下，顶点是原点而且是抛物线的最高点，对称轴是 y 轴
不同点：|a| 越大，抛物线的开口越小．
当x<0 (在对称轴的左侧)时，y随着x的增大而增大.
当x>0 (在对称轴的右侧)时，y随着x的增大而减小.
思考：二次函数 的增减性
1.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,y随着x的增大而增大；在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).
(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ；在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,当x 0时,y<0.
2.已知抛物线y=ax²经过点A（-2，-8）. （1）求此抛物线的函数表达式； （2）判断点B（-1，- 4）是否在此抛物线上. （3）求出此抛物线上纵坐标为-6的点的坐标.
a的绝对值越大，开口越小
关于y轴对称，对称轴是直线x＝0
顶点坐标是原点（0，0）
当x=0时，y最小值=0
当x=0时，y最大值=0
在对称轴左侧递减在对称轴右侧递增
在对称轴左侧递增在对称轴右侧递减
（1）其中开口向上的是________（填序号）；（2）其中开口向下且开口最大的是______（填序号）；（3）有最高点的是_______（填序号）.
习题 2 分别写出抛物线 与 的开口方向、对称轴及顶点坐标.
习题 3 已知一次函数 y=ax+b 和二次函数 y=ax2，其中a≠0，b<0，则下面选项中，图象可能正确的是（ ）
y=ax+b与y轴交点（0，b）
交点在 y轴负半轴，故B、D错；
已知二次函数y=x2，若x≥m时，y最小值为0，求实数m的取值范围．
解：∵二次函数y=x2， ∴当x=0时，y有最小值，且y最小值=0， ∵当x≥m时，y最小值=0， ∴m≤0．
已知二次函数y＝2x2.(1)若点(－2，y1)与(3，y2)在此二次函数的图象上，则 y1_____ y2；(填“>”“＝”或“<”)；(2)如图，此二次函数的图象经过点(0，0)，长方形ABCD的顶点A、B在x轴上，C、D恰好在二次函数的图象上，B点的横坐标为2，求图中阴影部分的面积之和．