






沪科版九年级上册22.2 相似三角形的判定精品ppt课件
展开1.掌握三角形相似的判定定理2,并熟练地运用;(重点)2.会准确地运用两个三角形相似的条件来判定两个三角形是否相似.(难点)
问题1 有两边对应成比例的两个三角形相似吗?
问题2 类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
改变 k 和∠A 的值的大小,是否有同样的结论?
探索1:两边成比例且夹角相等的两个三角形相似
如图,BC与DE 相交于点O.问: (1) 当∠B满足什么条件时,△ABC∽△ADE? (2) 当 AC:AE 满足什么条件时,△ABC∽△ADE?
(1) ∵ ∠A=∠A
(2) ∵ ∠A=∠A
∴ 当 AC:AE=AB:AD 时,
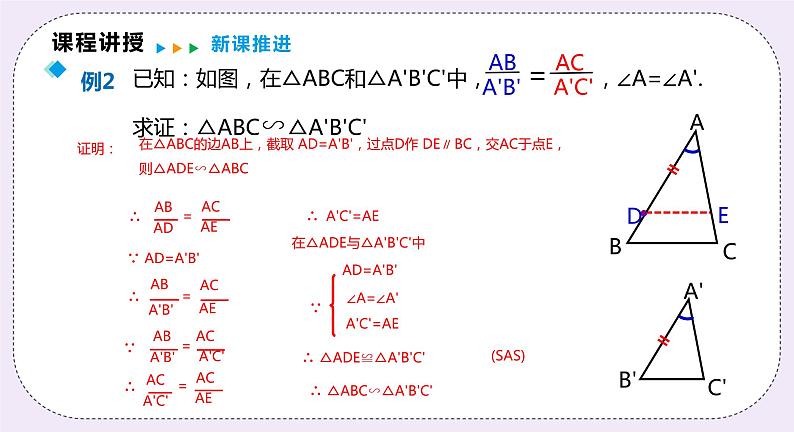
已知:如图,在△ABC和△A'B'C'中, ,∠A=∠A'.求证:△ABC∽△A'B'C'
相似三角形的判定 定理 2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
简记为:两边成比例且夹角相等的两个三角形相似.
利用该定理判定三角形相似时,必须注意是 两边及夹角,即相等的角必须是成比例的两边 的夹角否则不能判定两个三角形相似.
如果△ABC与△A'B'C'两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
【结论】判定两个三角形相似,角必须是两边的夹角.
在△ABC中,∠A=48°,AB=1.5cm,AC=2cm;在△DEF中,∠E=48°,DE=2.8cm,EF=2.1cm.问这两个三角形相似吗?为什么
利用两边成比例且夹角相等判定两个三角形相似的步骤:
① 找出两个三角形中相等的那个角;
② 再分别找出两个三角形中夹这个角的两条边,并按从小到大的排列找出对应边;
③ 最后看两组对应边是否成比例,若成比例则两个三角形相似,否则不相似.
如图,在△ABC中,点D,E分别在边 AB,AC上,∠AED=∠B. 射线AG分别交线段DE,BC于点F,G,且 .
(1) 求证:△ADF∽△ACG;
(2) 若 ,求 的值.
1. 在 △ABC 和 △DEF 中,∠C =∠F=70°,AC = 3.5 cm,BC = 2.5 cm,DF =2.1 cm,EF =1.5 cm. 求证:△DEF∽△ABC.
2. 如图,△ABC 与 △ADE 都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE. 求证:△ABC ∽△ADE.
证明:∵ △ABC 与 △ADE 是等腰三角形,∴ AD =AE,AB = AC,
又 ∵∠DAB = ∠CAE,∴ ∠DAB +∠BAE = ∠CAE +∠BAE,即 ∠DAE =∠BAC,∴△ABC ∽ △ADE.
解:∵ AE=1.5,AC=2,
3. 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
又∵∠EAD=∠CAB,∴ △ADE ∽△ABC,
提示:解题时要找准对应边.
在Rt△ABC中,两直角边分别为3cm,4cm;在Rt△A'B'C'中,斜边为25cm,一条直角边为15cm.问这两个直角三角形相似吗?为什么.
如图,△ACD和△ABC相似需具备的条件是( )
C. AC2=AD·AB
D. CD2=AD·BD
如图,在△ABC中,AB=16,AC=8,在AC上取一点D,使AD=5,如果在AB上取一点E,使△ADE和△ABC相似,求AE的长.
① 如图,当AD和AC是对应边时,△ADE∽△ACB
∵ AB=16,AC=8,AD=5
② 如图,当AD和AB是对应边时,
如图,在△ABC中,∠C=90°,BC=16cm,AC=12cm,点P从B出发沿BC以2cm/s的速度向C移动,点Q从C出发,以1cm/s的速度向A移动,若P、Q分别从B、C同时出发,设运动时间为ts,当为何值时,△CPQ与△CBA相似?
① 当CP和CB是对应边时,△CPQ∽△CBA
② 当CP和CA是对应边时,△CPQ∽△CAB
综上所述,当t=4.8秒或 秒时,△CPQ与△CBA相似.
如图,已知:△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且 AB= ,BC=1. 连接BF,分别交AC,DC,DE于点P,Q,R. (1) 求证:△BFG∽△FEG; (2) 求BF的长.
如图,D是△ABC内的一点,E是△ABC外一点,且 ∠1=∠2,∠3=∠4.
求证:(1) △ABD∽△CBE; (2) △ABC∽△DBE.
如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG. (1) 求证:△ACF∽△GCA;(2) 求∠AFB+∠AGB 的度数.
如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.
求证:△ADQ∽△QCP
又∵ ∠C=∠D=90°
∴ △ADQ∽△QCP
初中数学沪科版九年级上册22.2 相似三角形的判定精品课件ppt: 这是一份初中数学沪科版九年级上册22.2 相似三角形的判定精品课件ppt,共17页。PPT课件主要包含了学习目标及重难点,课程导入,课程讲授,课堂练习,习题1,习题2,习题3等内容,欢迎下载使用。
初中沪科版第22章 相似形22.2 相似三角形的判定精品ppt课件: 这是一份初中沪科版第22章 相似形22.2 相似三角形的判定精品ppt课件,共23页。PPT课件主要包含了学习目标及重难点,课程导入,课程讲授,随堂小练习,几何语言,课堂练习,习题1,习题2,cm3cm,习题3等内容,欢迎下载使用。
初中数学沪科版九年级上册22.2 相似三角形的判定优质ppt课件: 这是一份初中数学沪科版九年级上册22.2 相似三角形的判定优质ppt课件,共23页。PPT课件主要包含了复习导入,全等三角形,那这样变化一下呢,习题1,习题2,习题3,习题4,习题5等内容,欢迎下载使用。













