沪科版九年级上册第23章 解直角三角形23.1 锐角的三角函数精品ppt课件

这是一份沪科版九年级上册第23章 解直角三角形23.1 锐角的三角函数精品ppt课件，共25页。PPT课件主要包含了学习目标及重难点，课程导入，求下列三角函数的值，课程讲授，sin，cos，tan，ndF，sin-1，角度增大等内容，欢迎下载使用。
1.复习并巩固锐角三角函数的相关知识；2.学会利用计算器求三角函数值并进行相关计算；(重点)3.学会利用计算器根据三角函数值求锐角度数并计算.（难点）
sin 45°= ____
cs 60°= ____
tan 30°= ____
sin 36°= ____
任意一个锐角，如何求它的三角函数值呢？
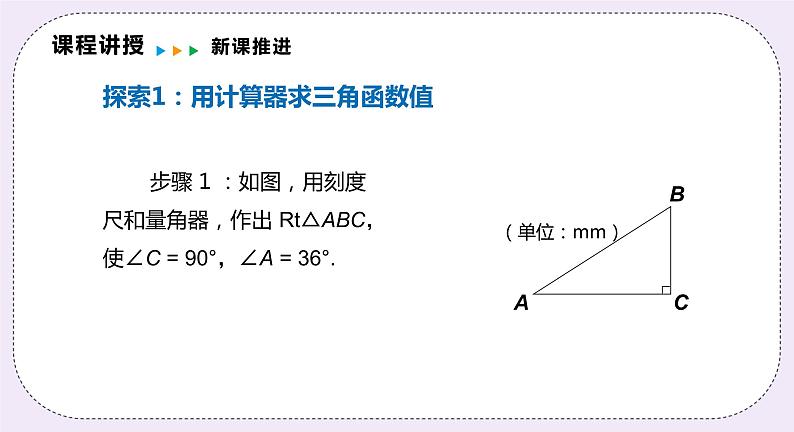
探索1：用计算器求三角函数值
步骤 1 ：如图，用刻度尺和量角器，作出 Rt△ABC，使∠C = 90°，∠A = 36°.
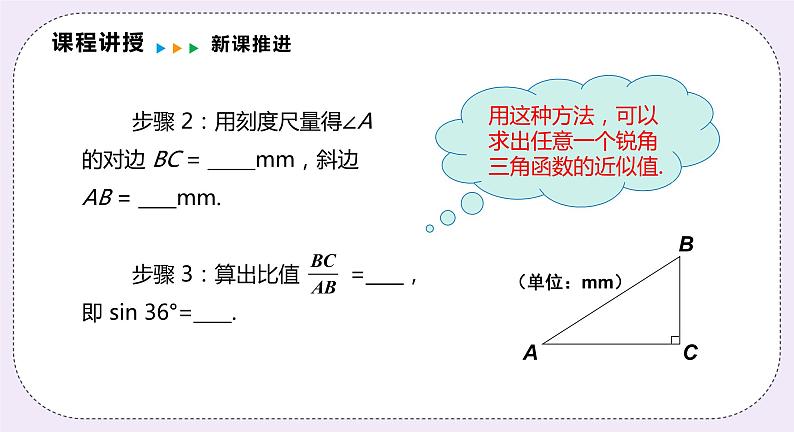
步骤 2：用刻度尺量得∠A 的对边 BC = _____mm，斜边AB = ____mm. 步骤 3：算出比值 =____，即 sin 36°=____.
求 sin 40°的值（精确到 0.000 1）.
∴ sin 40°= 0.642 8.
求值：（精确到 0.000 1）.（1）cs 34°35'，（2）tan 66°15'17''.
∴ cs 34°35' = 0.823 3.
（2）tan 66°15'17''.
∴ tan 66°15'17'' = 2.273 2
如果已知锐角三角函数值，也可以使用计算器求出相应的锐角．
探索2：利用计算器求锐角的度数
已知 sin A = 0.508 6，求锐角 A.
∴ ∠A = 30.570 6°= 30°34'14''
已知下列锐角三角函数值，用计算器求锐角∠A，∠B的度数(结果精确到0.1°)：(1)sinA＝0.7，sinB＝0.01；(2)csA＝0.15，csB＝0.8；(3)tanA＝2.4，tanB＝0.5.
解：(1)由sinA＝0.7，得∠A≈44.4°；由sinB＝0.01，得∠B≈0.6°；(2)由csA＝0.15，得∠A≈81.4°；由csB＝0.8，得∠B≈36.9°；(3)由tanA＝2.4，得∠A≈67.4°；由tanB＝0.5，得∠B≈26.6°.
cs55°= cs70°=cs74°28 '=
tan3°8 ' = tan80°25'43″=
sin20°=
sin35°=
sin15°32 ' =
比一比，你能得出什么结论？
正弦值随着角度的增大（或减小）而增大（或减小）
余弦值随着角度的增大（或减小）而减小（或增大）
正切值随着角度的增大（或减小）而增大（或减小）
如图，从A地到B地的公路需经过C地，图中AC＝10千米，∠CAB＝25°，∠CBA＝45°.因城市规划的需要，将在A、B两地之间修建一条笔直的公路．
(1)求改直后的公路AB的长；(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)?
(1)求改直后的公路AB的长；
解：(1)过点C作CD⊥AB于点D，∵AC＝10千米，∠CAB＝25°，∴CD＝AC·sin∠CAB＝10×sin25°≈10×0.42＝4.2(千米)，AD＝AC·cs∠CAB＝10×cs25°≈10×0.91＝9.1(千米)．∵∠CBA＝45°，∴BD＝CD＝4.2(千米)，
∴AB＝AD＋BD＝9.1＋4.2＝13.3(千米)．所以，改直后的公路AB的长约为13.3千米；
(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)?
(2)∵AC＝10千米，BC＝5.9千米，∴AC＋BC－AB＝10＋5.9－13.3＝2.6(千米)．所以，公路改直后该段路程比原来缩短了约2.6千米．
【方法总结】解决问题的关键是作出辅助线，构造直角三角形，利用三角函数关系求出有关线段的长．
如图，课外数学小组要测量小山坡上塔的高度DE，DE所在直线与水平线AN垂直．他们在A处测得塔尖D的仰角为45°，再沿着射线AN方向前进50米到达B处，此时测得塔尖D的仰角∠DBN＝61.4°，小山坡坡顶E的仰角∠EBN＝25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位)．
1. 用计算器求三角函数值：（精确到 0.000 1）
（1）sin 10°； （2）cs 50°18' .
2. 已知三角函数值，用计算器求锐角 A 和B：（精确到1'）
sin A = 0.708 3，
sin B = 0.568 8；
cs A = 0.829 0，
cs B = 0.993 1；
tan A = 0.913 1，
tan B = 31.80；
设 0°＜∠A＜∠B ＜ 90°，比较下列各组两个值的大小.（选填“＞”“＜”或“＝”）
（1）sin A____ sin B；（2）cs A ____cs B；（3）tan A____ tan B.
比较大小：sin37°，cs52°，sin41°.
解：解法一 ∵cs52°＝sin(90°－52°)＝sin38°，而37°＜38°＜41°，∴sin37°＜sin38°＜sin41°，即sin37°＜cs52°＜sin41°.解法二 ∵sin37°＝cs(90°－37°)＝cs53°，sin41°＝cs(90°－41°)＝cs49°，而49°＜52°＜53°，∴cs49°＞cs52°＞cs53°，即sin41°＞cs52°＞sin37°.
下列各式中一定成立的是（ ）A.tan75°﹥tan48°﹥tan15° B. tan75°﹤tan48°﹤tan15°C. cs75°﹥cs48°﹥cs15° D. sin75°﹤sin48°