



专题33 从全等到相似类比探究-2023年中考数学二轮复习核心考点专题提优拓展训练
展开专题33 从全等到相似类比探究(原卷版)
第一部分 典例剖析
类型一 从全等到相似——旋转变换
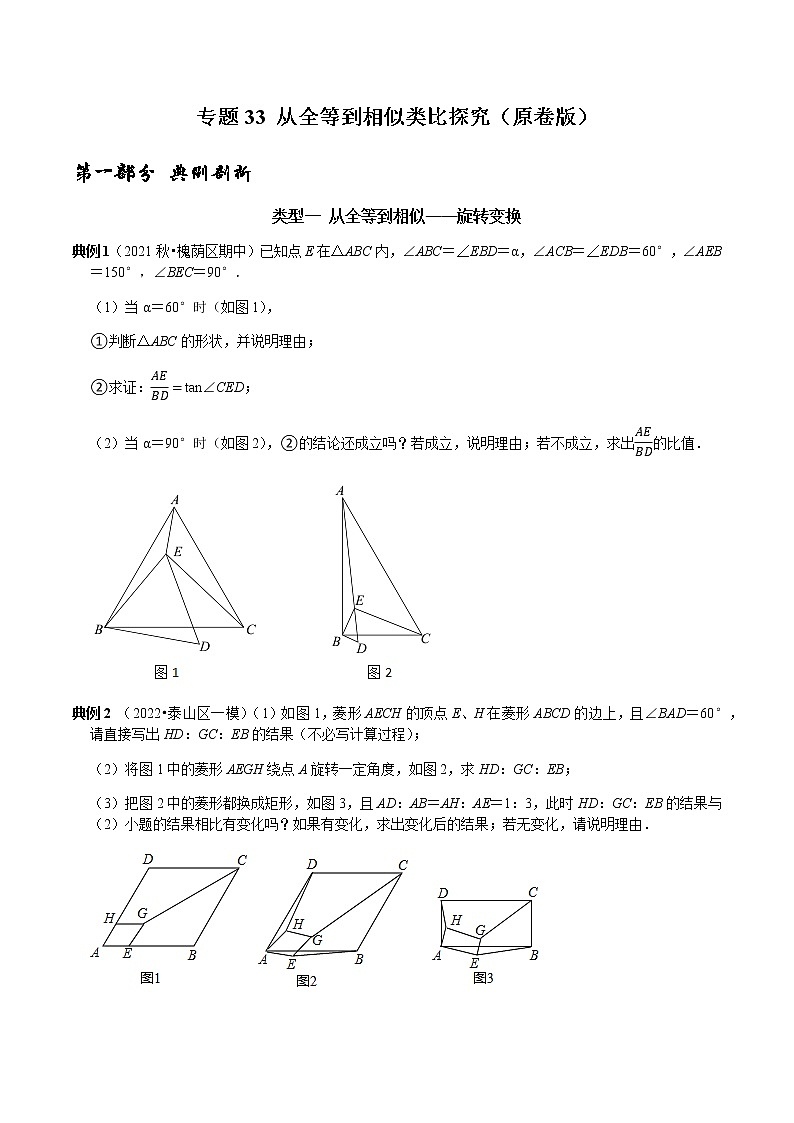
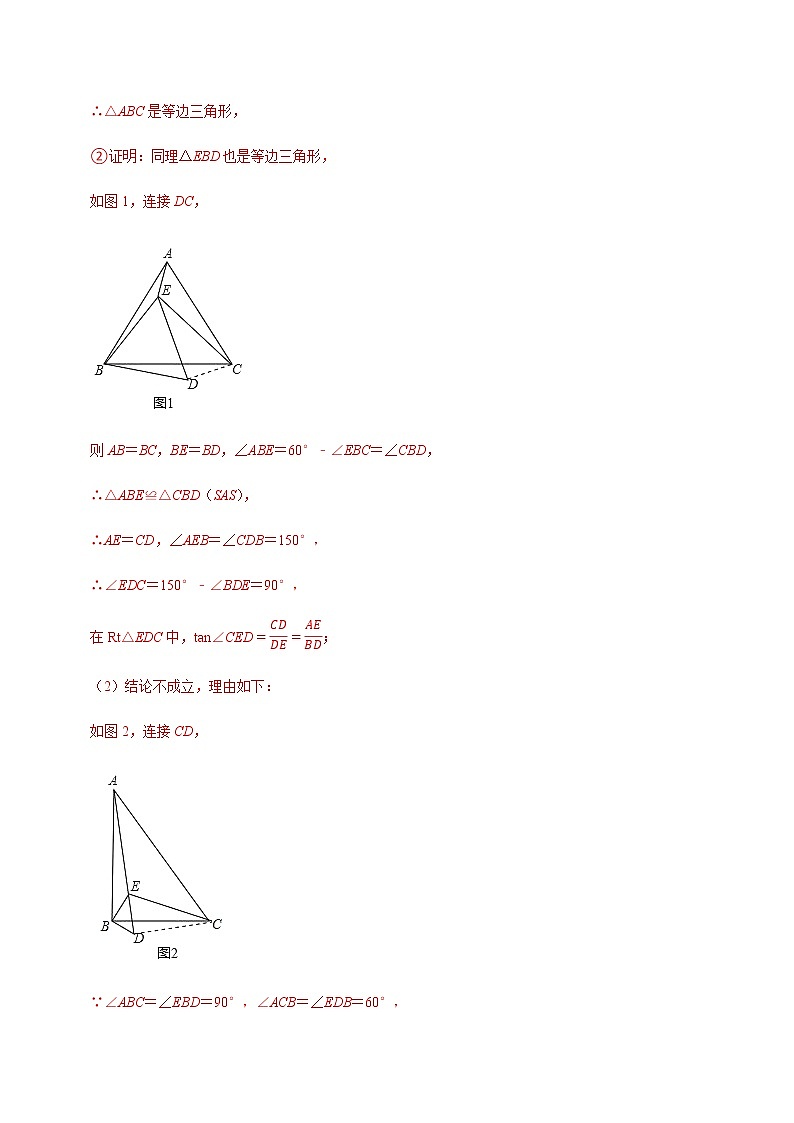
典例1(2021秋•槐荫区期中)已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:tan∠CED;
(2)当α=90°时(如图2),②的结论还成立吗?若成立,说明理由;若不成立,求出的比值.
典例2 (2022•泰山区一模)(1)如图1,菱形AECH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,请直接写出HD:GC:EB的结果(不必写计算过程);
(2)将图1中的菱形AEGH绕点A旋转一定角度,如图2,求HD:GC:EB;
(3)把图2中的菱形都换成矩形,如图3,且AD:AB=AH:AE=1:3,此时HD:GC:EB的结果与(2)小题的结果相比有变化吗?如果有变化,求出变化后的结果;若无变化,请说明理由.
典例3(2022•湘潭县校级模拟)如图1,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.
(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
①如图2,当点F落在AC上时(F不与C重合),若CF=1,tanC=3,求AE的长;
②如图3,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的数量关系,并说明理由.
典例4(2022•杭州模拟)已知,在等腰直角△ABC中,AB=AC,∠BAC=90°,点D为直线BC上的一动点(点D不与点B、C重合),连接AD,以AD为边向右作等腰直角△ADE,AD=AE,连接CE.
(1)填空:当点D在线段BC上如图(一),可通过证明①△ ≌△ ,得到BD= ,进而判断②CE,CD,BC三条线段的数量关系为 .
(2)当点D在线段BC的延长线上且其他条件不变如图(二),(1)中CE,CD,BC三条线段的数量关系是否仍然成立?如果成立,请说明理由;如果不成立,请写出你的结论,并证明.
(3)当点D在线段CB的延长线上且其他条件不变,请你构造出图形,并写出CE,CD,BC三条线段的数量关系.
类型二 从全等到相似——变式探究
典例5 (2022•坪山区一模)已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
问题发现:
(1)①如图1,若四边形ABCD是正方形,且DE⊥CF于G,则 ;
②如图2,当四边形ABCD是矩形时,且DE⊥CF于G,AB=m,AD=n,则 ;
拓展研究:
(2)如图3,若四边形ABCD是平行四边形,且∠B+∠EGC=180°时,求证:;
解决问题:
(3)如图4,若BA=BC=5,DA=DC=10,∠BAD=90°,DE⊥CF于G,请直接写出的值.
典例6 (2022秋•连山区校级月考)如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=90°,AC、BD交于点M.
(1)如图1,求证:AC与BD的数量与位置关系并说明理由;
(2)连接MO,求证:MO平分∠BMC;
(3)如图2,∠AOB=∠COD=60°时,直接写出∠AMD的度数.
类型三 从全等到相似——从特殊到一般
典例7 (2019春•方城县期中)问题:如图1,在平行四边形ABCD中,点E是BC边的中点,连接AE,点F是线段AE上一点,连接BF并延长,交射线CD于点G.若AF:EF=4:1,求的值.
(1)尝试探究:
如图1,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是.CG和EH的数量关系是,因此 .
(2)类比延伸:
在原题的条件下,若把“AF:EF=4:1”改为“AF:EF=n:1”(n>0),求的值.(用含有n的式子表示)
(3)拓展迁移:
如图2,在四边形ABCD中,CD∥AB,点E是BC的延长线上的一点,AE与BD相交于点F.若AB:CD=a:1(a>0),BC:BE=b:1(b>0),则 .(直接用含有a、b的式子表示,不写解答过程)
第二部分 专题提优训练
1.(2022春•金牛区校级月考)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2.连接AA1,CC1若AA1=4,求CC1的长;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1求线段EP1长度的最大值与最小值.
2.(2022秋•清镇市月考)如图1,矩形ABCD与矩形CEFG全等,点B,C,E和点C,D,G分别在同一直线上,且AB=CE=2,BC=EF=4,连接AC,CF.
(1)在图1中,连接AF,则AF= ;
(2)如图2,将图1中的矩形CEFG绕点C逆时针旋转,当CG平分∠ACF时,求点G到AC的距离;
(3)如图3,将图1中的矩形CEFG绕点C顺时针方向旋转,连接AF,DE,两线相交于点M,求证:点M是AF的中点.
3.(锦江区模拟)已知:在△ABC中,∠DBC=∠ACB,BC=2AC,BD=BC,CD交线段AB于点E.
(1)如图1,当∠ACB=90°时,求证:DE=2CE;
(2)当∠ACB=120°时,
①如图2,猜想线段DE、CE之间的数量关系并证明你的猜想;
②如图3,点F是BC边的中点,连接DF,DF与AB交于G,求的值.
4.(岳阳中考)已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连接AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).
(1)如图1,若AB=AC,求证:CD=2BE;
(2)如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);
(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连接EF交BC于点O,设△COE的面积为S1,△COF的面积为S2,求(用含α的式子表示).
5.(2018•武汉模拟)在菱形ABCD中,E、F分别为AB、BC边上的点,连接AF、DE,且∠ADE=∠BAF.
(1)若∠B=90°,求证:△ADE≌△BAF;
(2)若∠B=60°,求证:;
(3)若点E为AB的中点,AF⊥BC,请直接写出的值.
专题33 从全等到相似类比探究-2023年中考数学二轮复习核心考点拓展训练(解析版): 这是一份专题33 从全等到相似类比探究-2023年中考数学二轮复习核心考点拓展训练(解析版),共29页。试卷主要包含了从全等到相似——旋转变换,从全等到相似——变式探究,从全等到相似——从特殊到一般等内容,欢迎下载使用。
专题33 从全等到相似类比探究-2023年中考数学二轮专题提升训练: 这是一份专题33 从全等到相似类比探究-2023年中考数学二轮专题提升训练,共33页。试卷主要包含了从全等到相似——旋转变换,从全等到相似——变式探究,从全等到相似——从特殊到一般等内容,欢迎下载使用。
专题32 中考热点规律探究填空选择专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练: 这是一份专题32 中考热点规律探究填空选择专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练,文件包含专题32中考热点规律探究填空选择专项训练解析版docx、专题32中考热点规律探究填空选择专项训练原卷版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。