2023年中考数学二轮复习选填专题复习专题五：规律探索题

这是一份2023年中考数学二轮复习选填专题复习专题五：规律探索题，文件包含2023年中考数学二轮复习选填专题复习解析版docx、2023年中考数学二轮复习选填专题复习原卷版docx等2份试卷配套教学资源，其中试卷共113页， 欢迎下载使用。

2022-2023学年二轮复习选填专题五：
规律探索题
方法点睛
一、与坐标系结合的图形变化规律型问题
根据图形点坐标的变换特点，可知这类题有两种考查形式：一类是点坐标变换是在同一象限递推变化；另一类是点坐标变换在坐标轴上或象限内循环递推变化．
解决这类题的方法如下：
1．根据图形点坐标的变化特点判断出属于哪一类．
2．根据图形的变换规律分别求出第1个点、第2个点、第3个点、第4个点的坐标，归纳出后一个点坐标与前一个点坐标之间存在的倍分关系．
3．(1)第一类确定点坐标的方法：根据上述得到的倍分关系，得到第M个点的坐标；(2)第二类确定点坐标的方法：先观察点坐标变换的规律是按顺时针循环，还是按逆时针循环交替出现，找出循环一周的变换次数，记为n，用M÷n＝w……q(0≤q＜n)，则第M次变换同第q次变换后的点坐标所在的坐标轴或象限相同，根据已得到的倍分关系，得到第M个点的坐标．
二、对于数式规律型，解决的方法是先找共同点，再找变化点，得到规律后用代数式去表示．
三、图形规律型一般考查图形的个数，而图形个数大都与序号有关，猜想规律与”序号”之间的对应关系并用关于”序号”的式子表示出变化规律．
在探究规律时，往往用到以下拆分技巧和求和公式：
①拆分技巧：＝－.
②正整数求和：1＋2＋3＋…＋n＝(n≥1)；
奇数求和：1＋3＋5＋…＋(2n－1)＝n2(n≥1)；
偶数求和：2＋4＋6＋…＋2n＝n(n＋1)(n≥1)．
典例分析
类型一　图形循环(周期)变化规律
例1　（2022河南中考）如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合，轴，交y轴于点P．将△OAP绕点O顺时针旋转，每次旋转90°，则第2022次旋转结束时，点A的坐标为（ ）


A. B. C. D.
【答案】B
【解析】
【分析】首先确定点A的坐标，再根据4次一个循环，推出经过第2022次旋转后，点A的坐标即可．
【详解】解：正六边形ABCDEF边长为2，中心与原点O重合，轴，
∴AP＝1， AO＝2，∠OPA＝90°，
∴OP＝＝，
∴A（1，），
第1次旋转结束时，点A的坐标为（，-1）；
第2次旋转结束时，点A的坐标为（-1，）；
第3次旋转结束时，点A的坐标为（，1）；
第4次旋转结束时，点A的坐标为（1，）；
∵将△OAP绕点O顺时针旋转，每次旋转90°，
∴4次一个循环，
∵2022÷4＝505……2，
∴经过第2022次旋转后，点A的坐标为（-1，），
故选：B
【点睛】本题考查正多边形与圆，规律型问题，坐标与图形变化﹣旋转等知识，解题的关键是学会探究规律的方法，属于中考常考题型．
类型二　图形成倍递推变化规律
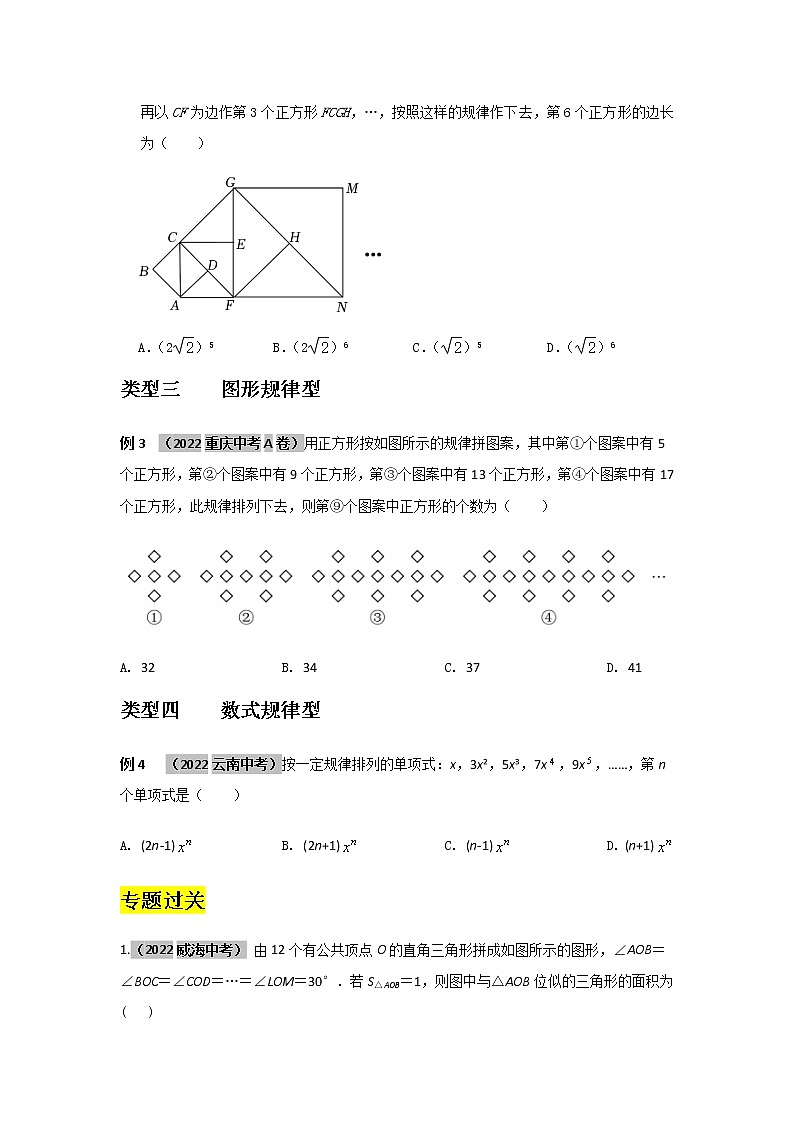
例2： （2022烟台中考）如图，正方形ABCD边长为1，以AC为边作第2个正方形ACEF，再以CF为边作第3个正方形FCGH，…，按照这样的规律作下去，第6个正方形的边长为（　　）

A．（2）5 B．（2）6 C．（）5 D．（）6
【分析】根据勾股定理得出正方形的对角线是边长的．第1个正方形的边长为1，其对角线长为；第2个正方形的边长为，其对角线长为（）2；第3个正方形的边长为（）2，其对角线长为（）3；•••；第n个正方形的边长为（）n﹣1.所以，第6个正方形的边长（）5．
【解答】解：由题知，第1个正方形的边长AB＝1，
根据勾股定理得，第2个正方形的边长AC＝，
根据勾股定理得，第3个正方形的边长CF＝（）2，
根据勾股定理得，第4个正方形的边长GF＝（）3，
根据勾股定理得，第5个正方形的边长GN＝（）4，
根据勾股定理得，第6个正方形的边长＝（）5．
故选C．
【点评】本题利用勾股定理找到正方形边长之间的倍关系，由此依次推出第2个、第3个、•••、第6个正方形的边长．
类型三 图形规律型
例3 （2022重庆中考A卷）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（ ）

A. 32 B. 34 C. 37 D. 41
【答案】C
【解析】
【分析】第1个图中有5个正方形，第2个图中有9个正方形，第3个图中有13个正方形，……，由此可得：每增加1个图形，就会增加4个正方形，由此找到规律，列出第n个图形的算式，然后再解答即可．
【详解】解：第1个图中有5个正方形；
第2个图中有9个正方形，可以写成：5+4=5+4×1；
第3个图中有13个正方形，可以写成：5+4+4=5+4×2；
第4个图中有17个正方形，可以写成：5+4+4+4=5+4×3；
．．．
第n个图中有正方形，可以写成：5+4（n-1）=4n+1；
当n=9时，代入4n+1得：4×9+1=37．
故选：C．
【点睛】本题主要考查了图形的变化规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键．
类型四 数式规律型
例4 （2022云南中考）按一定规律排列的单项式：x，3x²，5x³，7x，9x，……，第n个单项式是（ ）
A. (2n-1) B. (2n+1) C. (n-1) D. (n+1)
【答案】A
【解析】
【分析】系数绝对值均为奇数，可用(2n-1)表示；字母和字母的指数可用xn表示．
【详解】解：依题意，得第n项为（2n-1）xn，
故选：A．
【点睛】本题考查的是单项式，根据题意找出规律是解答此题的关键．
专题过关
1.（2022威海中考） 由12个有公共顶点O的直角三角形拼成如图所示的图形，∠AOB＝∠BOC＝∠COD＝…＝∠LOM＝30°．若S△AOB＝1，则图中与△AOB位似的三角形的面积为( )


A. （）3 B. （）7 C. （）6 D. （）6
【答案】C
【解析】
【分析】根据题意得出A、O、G在同一直线上，B、O、H在同一直线上，确定与△AOB位似的三角形为△GOH，利用锐角三角函数找出相应规律得出OG=，再由相似三角形的性质求解即可．
【详解】解：∵∠AOB＝∠BOC＝∠COD＝…＝∠LOM＝30°
∴∠AOG＝180°，∠BOH＝180°，
∴A、O、G在同一直线上，B、O、H在同一直线上，
∴与△AOB位似的三角形为△GOH，
设OA=x，
则OB=，
∴OC=，
∴OD=，
…
∴OG=，
∴，
∴，
∵，
∴，
故选：C．
【点睛】题目主要考查利用锐角三角函数解三角形，找规律问题，相似三角形的性质等，理解题意，找出相应边的比值规律是解题关键．
2. （2022荆州中考）如图，已知矩形ABCD的边长分别为a，b，进行如下操作：第一次，顺次连接矩形ABCD各边的中点，得到四边形；第二次，顺次连接四边形各边的中点，得到四边形；…如此反复操作下去，则第n次操作后，得到四边形的面积是（ ）


A. B. C. D.
【答案】A
【解析】
【分析】利用中位线、菱形、矩形的性质可知，每一次操作后得到的四边形面积为原四边形面积的一半，由此可解．
【详解】解：如图，连接AC，BD，，．


∵ 四边形ABCD是矩形，
∴，，．
∵ ，，，分别是矩形四个边的中点，
∴，
∴，
∴四边形是菱形，
∵ ，，
∴四边形的面积为：．
同理，由中位线的性质可知，
，，
，，
∴四边形是平行四边形，
∵，
∴，
∴四边形是矩形，
∴四边形的面积为：．
∴每一次操作后得到四边形面积为原四边形面积的一半，
∴四边形的面积是．
故选:A．
【点睛】本题考查矩形的性质，菱形的性质以及中位线的性质，证明四边形是菱形，四边形是矩形是解题的关键．
3．（2022广州中考）（3分）如图，用若干根相同的小木棒拼成图形，拼第1个图形需要6根小木棒，拼第2个图形需要14根小木棒，拼第3个图形需要22根小木棒……若按照这样的方法拼成的第n个图形需要2022根小木棒，则n的值为（　　）

A．252 B．253 C．336 D．337
【分析】根据图形特征，第1个图形需要6根小木棒，第2个图形需要6×2+2＝14根小木棒，第3个图形需要6×3+2×2＝22根小木棒，按此规律，得出第n个图形需要的小木棒根数即可．
【解答】解：由题意知，第1个图形需要6根小木棒，
第2个图形需要6×2+2＝14根小木棒，
第3个图形需要6×3+2×2＝22根小木棒，
按此规律，第n个图形需要6n+2（n﹣1）＝（8n﹣2）个小木棒，
当8n﹣2＝2022时，
解得n＝253，
故选：B．
【点评】本题主要考查了图形的变化规律，解决问题的关键是由特殊找到规律：第n个图形需要（8n﹣2）个小木棒是解题的关键．
4. （2022济宁中考） 如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（ ）

A. 297 B. 301 C. 303 D. 400
【答案】B
【解析】
【分析】首先根据前几个图形圆点的个数规律即可发现规律，从而得到第100个图摆放圆点的个数．
【详解】解：观察图形可知：第1幅图案需要4个圆点，即4＋3×0，
第2幅图7个圆点，即4+3=4+3×1；
第3幅图10个圆点，即4＋3＋3=4＋3×2；
第4幅图13个圆点，即4＋3＋3＋3=4＋3×3；
第n幅图中，圆点的个数为：4+3(n-1)=3n+1，
……，
第100幅图，圆中点的个数为：3×100+1=301．
故选：B．
【点睛】本题主要考查了图形的变化规律，解答的关键是由所给的图形总结出存在的规律．
5．（2022江西中考）（3分）将字母“”，“ ”按照如图所示的规律摆放，依次下去，则第4个图形中字母“”的个数是　　


A．9 B．10 C．11 D．12
【分析】列举每个图形中的个数，找到规律即可得出答案．
【解答】解：第1个图中的个数为4，
第2个图中的个数为，
第3个图中的个数为，
第4个图中的个数为，
故选：．
【点评】本题考查了规律型：图形的变化类，通过列举每个图形中的个数，找到规律：每个图形比上一个图形多2个是解题的关键．
6. （2022年重庆中考B卷） 把菱形按照如图所示的规律拼图案，其中第①个图案中有1个菱形，第②个图案中有3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（ ）

A 15 B. 13 C. 11 D. 9
【答案】C
【解析】
【分析】根据第①个图案中菱形的个数：；第②个图案中菱形的个数：；第③个图案中菱形的个数：；…第n个图案中菱形的个数：，算出第⑥个图案中菱形个数即可．
【详解】解：∵第①个图案中菱形的个数：；
第②个图案中菱形的个数：；
第③个图案中菱形的个数：；
…
第n个图案中菱形的个数：，
∴则第⑥个图案中菱形的个数为：，故C正确．
故选：C．
【点睛】本题主要考查的是图案的变化，解题的关键是根据已知图案归纳出图案个数的变化规律．
7. （2022牡丹江中考）观察下列数据：，，，，，…，则第12个数是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】仔细观察给出的一列数字，从而可发现，分子等于其项数，分母为其所处的项数的平方加1，根据规律解题即可．
【详解】解：，，，，，…，根据规律可得第n个数是，
∴第12个数是，
故选：D．
【点睛】本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．
8. （2022鄂州中考） 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n来表示．即：21＝2，22＝4，23＝8，24＝16，25＝32，……，请你推算22022的个位数字是（ ）
A. 8 B. 6 C. 4 D. 2
【答案】C
【解析】
【分析】利用已知得出数字个位数的变化规律进而得出答案．
【详解】解：∵21＝2，22＝4，23＝8，24＝16，25＝32，…，
∴尾数每4个一循环，
∵2022÷4＝505……2，
∴22022的个位数字应该是：4．
故选：C．
【点睛】此题主要考查了尾数特征，根据题意得出数字变化规律是解题关键．
9. （2022新疆兵团中考）将全体正偶数排成一个三角形数阵：

按照以上排列的规律，第10行第5个数是（ ）
A. 98 B. 100 C. 102 D. 104
【答案】B
【解析】
【分析】观察数字的变化，第n行有n个偶数，求出第n行第一个数，故可求解．
【详解】观察数字的变化可知：
第n行有n个偶数，
因为第1行的第1个数是： ；
第2行的第1个数是： ；
第3行的第1个数是：；
…
所以第n行的第1个数是： ，
所以第10行第1个数是：，
所以第10行第5个数是： ．
故选：B．
【点睛】本题考查了数字的规律探究，推导出一般性规律是解题的关键．
10.（2022河南上蔡三模） 如图，在平面直角坐标系中，正方形ABCD的顶点A的坐标是，顶点B的坐标是，对角线AC，BD的交点为M．将正方形ABCD绕着原点O逆时针旋转，每次旋转45°，则第2022次旋转结束时，点M的坐标为（ ）

A. B. C. D.
【答案】D
【解析】
【分析】过点D作轴，垂足为N，证明．求出点D的坐标为．进一步求出点M的坐标为．分析可知点M旋转一周需要旋转（次），利用，，可知第2022次旋转结束时和第6次旋转结束时，点M的坐标相同，且此时点M的位置就是绕点O逆时针旋转270°（或顺时针旋转90°）的位置．故可知点M的坐标为．
【详解】解：∵，，
∴，．
过点D作轴，垂足N，如解图所示，

则．
∵四边形ABCD为正方形，
∴，．
∴．
∴．
∴，．
∴点D的坐标为．
∵点M为BD的中点，
∴点M的坐标为．
由题意，可知正方形ABCD绕着原点O逆时针旋转，每次旋转45°，点M也绕着原点O逆时针旋转，每次旋转45°，则点M旋转一周需要旋转（次）．
又∵，，
∴第2022次旋转结束时和第6次旋转结束时，点M的坐标相同，且此时点M的位置就是绕点O逆时针旋转270°（或顺时针旋转90°）的位置．
∴第2022次旋转结束时，点M的坐标为，
故选：D．
【点睛】本题考查坐标与旋转规律，正方形性质，全等三角形的判定及性质，解题的关键是理解第2022次旋转结束时和第6次旋转结束时，点M的坐标相同，且此时点M的位置就是绕点O逆时针旋转270°（或顺时针旋转90°）的位置．
11. （2022河南长垣一模）如图，在菱形ABCD中，∠BAD＝60°，AB＝，点A，C在直线y＝x上，且点A的坐标为（，）．将菱形ABCD绕原点O逆时针旋转，每次旋转45°，则第85次旋转结束时，点C的坐标为（　　）

A. （，0） B. （0，2） C. （0，） D. （2，0）
【答案】B
【解析】
【分析】设菱形对角线AC与BD交于点E，根据题意得，，，根据锐角三角函数得，即可得，OC=2，分别求出第一次、第三次、第五次时点C的坐标，由题意得8次旋转为一个循环，第85次旋转结束时，点C的坐标与第五次旋转后点C的坐标相同，即可得．
【详解】解：如图所示，设菱形对角线AC与BD交于点E，

∵点，点A，C在直线上，
∴，，
∵，，四边形ABCD是菱形，
∴，
∴，
∴，
∴，
∴第一次旋转45°，点C的坐标为（0，-2），
第三次旋转45°，点C的坐标为（2，0），
第五次旋转45°，点C的坐标为（0，2），
由题意得8次旋转为一个循环，
∵，
∴第85次旋转结束时，点C的坐标与第五次旋转后点C的坐标相同，为（0，2），
故选：B．
【点睛】本题考查了一次函数的性质，菱形的性质，点的坐标，锐角三角函数，解题的关键是掌握这些知识点．
12.（2022河南虞城二模） 如图，平面直角坐标系中，，，第一次操作：将正方形绕点B顺时针旋转45°，得到正方形；第二次操作：将正方形绕点B顺时针旋转45°，得到正方形，这样一直延续这种操作，当得到正方形时，点的坐标为（ ）

A. B. C. D.
【答案】D
【解析】
【分析】由正方形的性质和旋转的性质探究规律，利用规律解决问题即可．
【详解】解：如图，过作

∵四边形OA1BC1是正方形，，，
OA＝2，
将正方形绕点B顺时针旋转45°，得到正方形；
则

每次旋转45°
360°÷45°=8，8次一循环

点的坐标与点重合
即与关于对称

故选D
【点睛】本题考查了正方形的性质、旋转的性质、坐标与图形的变化、规律型：点的坐标等知识，解题的关键是学会从特殊到一般的探究规律的方法．
13. （2022河南商城一模）如图，在平面直角坐标系中放置一菱形OABC，已知∠ABC＝60°，点B在y轴上，OA＝1，将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2021次，点B的落点依次为B1，B2，B3，……，则B2021的坐标为（　　）

A. （1010，0） B. （1345，） C. （，） D. （1346，0）
【答案】C
【解析】
【分析】根据题中的变换方式画出第5次，第6次，第7次，翻转后的图形，由图可知，每翻转6次，图形向右平移4个单位长度根据变化规律写出B2021的坐标即可．
【详解】
解：如图，连接，
∵四边形是菱形，
∴，
∵，
∴是等边三角形，
∴，
∴，
∵，
∴，
画出第5次，第6次，第7次，翻转后的图形，
由图可知，每翻转6次，图形向右平移4个单位长度，
∵2021=336×6＋5，
∴点向右平移1344（即336×4）个单位长度到点，
∵点的坐标为，
∴点的坐标为，
∴点坐标为，
故选：C．
【点睛】本题考查菱形的性质，图形的旋转变换，点的坐标规律探索，能够发现规律，总结规律，应用规律是解决本题的关键．
14. （2022河南西平一模）如图，在平面直角坐标系中，菱形OABC的顶点B在x轴上，且cm，．点D从点O出发，沿O→A→B→C→O以2cm/s的速度做环绕运动，则第85秒时，点D的坐标为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】利用菱形的性质证得△AOB是等边三角形，得到OA=OB=8cm，∠OBA=60°，进而得到点D从点O出发以2cm/s的速度做环绕运动，16秒为一个循环，确定第85秒时点D在AB边上，且，过点D作DH⊥x轴于H，利用三角函数求出BH，得到第85秒时，点D的坐标．
【详解】解：∵四边形OABC是菱形，
∴OA=AB=BC=OC，
∵，
∴△AOB是等边三角形，
∴OA=OB=8cm，∠OBA=60°，
∵，
∴点D从点O出发以2cm/s的速度做环绕运动，16秒为一个循环，
∵，
∴第85秒时点D在AB边上，且，
∴，
过点D作DH⊥x轴于H，
∴，
∴OH=8-3=5，
∴第85秒时，点D的坐标为，
故选：C．

【点睛】此题考查了菱形的性质，等边三角形的判定及性质，锐角三角函数，点坐标的规律问题，正确理解菱形的性质证得△AOB是等边三角形是解题的关键．
15.（2022河南天一大联考） 如图，在平面直角坐标系中，OA1＝OB1，∠A1OB1＝120°，将ΔA1OB1绕点O顺时针旋转并且按一定规律放大，每次变化后得到的图形仍是顶角为120°的等腰三角形．第一次变化后得到等腰三角形A2OB2，点A1（1，0）的对应点为；第二次变化后得到等腰三角形A3OB3，点A2的对应点为；第三次变化后得到等腰三角形A4OB4，点A3的对应点为A4（4，0）⋯⋯依此规律，则第2022个等腰三角形中，点B2022的坐标是（　　）

A. （2022，0） B.
C. D.
【答案】D
【解析】
【分析】利用循环的规律，找到第2022个等腰三角形与第一个循环的图形的第几个位置相同，再根据第一个循环中的点坐标进行求值即可．
【详解】解：由题意可知，旋转规律为4次一个循环，
即第2022次为：505个循环余2，
∴点B2022位置与B3相同，在第三象限，
∵B3坐标为，
∴点B2022坐标为，即为．
故选：D．
【点睛】本题主要考查的是坐标系与几何图形的规律问题，准确找到循环规律是解题的关键．
16. （2022河南实验中学一模）如图，已知菱形OABC的顶点O(0，0)，B(2，2)，菱形的对角线的交于点D；若将菱形OABC绕点O逆时针旋转，每秒旋转45°，从如图所示位置起，经过60秒时，菱形的对角线的交点D的坐标为（ ）

A. (1，1) B. (﹣1，﹣1) C. (-1，1) D. (1，﹣1)
【10题答案】
【答案】B
【解析】
【分析】分别过点和点作轴于点，作轴于点，根据菱形的性质以及中位线的性质求得点的坐标，进而计算旋转的度数，7.5周，进而根据中心对称求得点旋转后的D坐标
【详解】如图，分别过点和点作轴于点，作轴于点，

∴，
∵四边形为菱形，
∴点为的中点，
∴点为的中点，
∴，，
∵，
∴；
由题意知菱形绕点逆时针旋转度数为：，
∴菱形绕点逆时针旋转周，
∴点绕点逆时针旋转周，
∵，
∴旋转60秒时点的坐标为．
故选B
【点睛】根据菱形的性质及中点的坐标公式可得点D坐标，再根据旋转的性质可得旋转后点D的坐标，熟练掌握菱形的性质及中点的坐标公式、中心对称的性质是解题的关键．
17. （2022河南虞城二模）如图，平面直角坐标系中，菱形的顶点，，将菱形以点O为旋转中心顺时针旋转，得到菱形，则点A的对应点D的坐标为（ ）

A B. C. D.
【答案】B
【解析】
【分析】过点作轴，根据题意求得的长，进而可得，即可求得点的坐标
【详解】解：过点作轴，如图，

四边形是菱形，，是对角线，且在轴上，
，

将菱形以点O为旋转中心顺时针旋转，
，


是等腰直角三角形

在第四象限，

故选B
【点睛】本题考查了菱形的性质，旋转的性质，坐标与图形，解直角三角形，掌握以上知识是解题的关键．
18. （2022商丘二模） 如图，在平面直角坐标系中，已知点，点B在第一象限内，，，将绕点O逆时针旋转，每次旋转60°，则第2022次旋转后，点B的坐标为（ ）

A. B. C. D.
【答案】B
【解析】
【分析】求出B1～B5的坐标，探究规律，利用规律解决问题即可．
【详解】解：过点B作BH⊥y轴于H．

在Rt△ABH中，∠AHB=90°，∠BAH=180°-120°=60°，AB=OA=2，
∴AH=AB•cos60°=1，BH=AH=，
在Rt△OBH中，，
∴∠BOH=30°，
∴，B（，3），
由题意B1（−，3），B2（−2，0），B3（-，-3），B4（，-3），B5（2，0），…，旋转6次是一个循环，
∵，
∴B2022（，3），
故选：B．
【点睛】本题考查坐标与图形变化-旋转，解直角三角形等知识，解题的关键是学会探究规律的方法，属于中考常考题型．
19. （2022三门峡一模）如图，直线与x轴、y轴分别相交于点A，B，过点B作，使．将绕点O顺时针旋转，每次旋转90°，当第2022次旋转结束时，点C的对应点落在反比例函数的图象上，则k的值为（ ）

A. -40 B. 40 C. 80 D. -80
【答案】C
【解析】
【分析】过点C作CD⊥y轴于点D，可证得△AOB∽△BDC，从而得到，再分别求出OA=3，OB=4，然后根据，可得，从而得到点C的坐标为（8，10），再根据将绕点O顺时针旋转，每次旋转90°，可得到旋转4次一个循环，从而得到当第2022次旋转结束时，此时点C的对应点落在第三象限，且与（8，10）关于原点对称，即可求解．
【详解】解：如图，过点C作CD⊥y轴于点D，

根据题意得：∠AOB=∠BDC=90°，
∴∠ABO+∠BAO=90°，
∵，
∴∠ABC=90°，
∴∠ABO+∠CBD=90°，
∴∠BAO=∠CBD，
∴△AOB∽△BDC，
∴，
∵直线与x轴、y轴分别相交于点A，B，
当x=0时，y=4，
当y=0时，x=3，
∴点A（3，0） ，B（0，4），
∴OA=3 ，OB=4，
∵．
∴，
解得：CD=8，BD=6，
∴OD=10，
∴点C的坐标为（8，10），
∵将绕点O顺时针旋转，每次旋转90°，
∴旋转4次一个循环，
∵，
∴当第2022次旋转结束时，此时点C的对应点落在第三象限，且与（8，10）关于原点对称，
∴此时，
∵点落在反比例函数的图象上，
∴k=80．
故选：C
【点睛】本题主要考查了图形的旋转，相似三角形的判定和性质，一次函数和反比例函数的图象和性质，明确题意，准确得到规律是解题的关键．
20.（2022南阳淅川一模） 如图，在中，，，顶点的坐标为．将绕点逆时针旋转，每次旋转90°，则第2022次旋转结束时，点的坐标为（ ）


A. B. C. D.
【答案】D
【解析】
【分析】根据已知条件求出AB，OB的长，再根据等面积法求出BM的长，确定出点B的坐标，以此类推，分别求出，，的坐标，找到规律计算即可；
【详解】如图所示，过点B作BM⊥y轴，


∵顶点的坐标为，
∴，
∵，，
∴，
设，，
∴，
∴，
∴，
∴，，
∴，
∴，
∴，
∴，
∴，
∵将绕点逆时针旋转，每次旋转90°，
∴，，，，
∴每4次一个循环，
∵，
∴第2022次旋转结束时，点的坐标为．
故选D．
【点睛】本题主要考查了坐标与图形旋转变化，探索点的坐标规律题型，解直角三角形的知识点，准确分析计算是解题的关键．
21. （2022南阳西峡一模）如图，矩形ABCD的顶点A、B在两坐标轴上，OA=OB=2，BC=．将矩形ABCD绕原点顺时针每次旋转90°，则第2022次旋转后点C的坐标是（ ）

A. （3，-5） B. （-5，-3） C. （-3，5） D. （5，3）
【答案】B
【解析】
【分析】如图所示，过点C作CF⊥x轴于F，先求出点C的坐标为（5，3），然后根据每四次旋转（即旋转360°）点C会回到初始位置，可知当旋转2022次时相当于把点C绕原点顺时针旋转180°，由此求解即可．
【详解】解：如图所示，过点C作CF⊥x轴于F，
∵OA=OB=2，∠AOB=90°，
∴∠AOB=∠CFB=90°，∠OBA=45°，，
∵四边形ABCD是矩形，
∴∠ABC=90°，
∴∠FBC=45°，
∴∠FCB=45°=∠FBC，
∴FB=FC，
∵，
∴，
∴FB=FC=3，
∴OF=5，
∴点C的坐标为（5，3），
∵将矩形ABCD绕原点顺时针每次旋转90°，
∴每四次旋转（即旋转360°）点C会回到初始位置，
∵2022÷4=505余2，
∴当旋转2022次时相当于把点C绕原点顺时针旋转180°，
∴此时C点的位置与初始位置关于原点对称，
∴第2022次旋转后点C的坐标是（-5，-3），
故选B．

【点睛】本题主要考查了坐标与图形，点的坐标规律探索，关于原点对称的点的坐标特征，正确分析出第2022此旋转后点C的位置是解题的关键．
22. （2022南阳卧龙二模）如图，正方形的四个顶点均在坐标轴上，．将正方形绕点顺时针旋转，每秒旋转，同时点P从的中点处出发，在正方形的边上顺时针移动，每秒移动1个单位，则第2022秒时，点的坐标为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】正方形绕原点沿顺时针方向每秒旋转，旋转一周需要6秒，，第2022秒时正方形回到初始位置；点P每秒移动1个单位，移动一周需要8秒，，第2022秒时点P移动到第三象限的位置，作于点E，根据点P为中点，得到．根据正方形的性质可知，得到，根据，得到，．得到点P的坐标为．
【详解】∵正方形每秒旋转，
∴每6秒旋转一周，
∵，
∴第2022秒时正方形回到初始位置；
∵点P每秒移动1个单位，
∴每8秒移动一周，
∵，
∴第2022秒时点P移动到如图所示的位置，
过点P作于点E，
∵点P为中点，
∴,
由正方形的性质可知，
∴，
∵，
∴．
∴．
∴点P的坐标为．
故选C．

【点睛】本题主要考查了正方形旋转，动点移动，熟练掌握正方形的边的性质，旋转图形的全等性质，动点移动路线形状与移动速度的性质，是解决本题的关键．
23.（2022洛阳一模） 如图，在平面直角坐标系xOy中，正方形ABCD的顶点，，规定把正方形ABCD“先沿y轴翻折，再向下平移1个单位”为一次变换，这样连续经过2022次变换后，正方形ABCD的中心的坐标为（ ）


A. B. C. D.
【答案】D
【解析】
【分析】根据正方形ABCD的顶点A（1，-1），B（3，-1），可得AB＝BC＝2，C（3，-3），先求出前几次变换后正方形ABCD的中心的坐标，根据变化规律求解即可．
【详解】解：∵正方形ABCD的顶点A（1，-1），B（3，-1），
∴AB＝BC＝2，
∴C（3，-3），正方形ABCD的中心的坐标为（2，-2）
一次变换后，正方形ABCD的中心的坐标为（-2，-3），
二次变换后，正方形ABCD的中心的坐标为（2，-4），
三次变换后，正方形ABCD的中心的坐标为（-2，﹣5），
…，
通过观察得：翻折次数为奇数时正方形ABCD的中心的横坐标为﹣2，翻折次数为偶数时正方形ABCD的中心的横坐标为2，变换一次，正方形ABCD的中心的纵坐标向下移一个单位，
∵2022是偶数，
∴正方形ABCD的中心的横坐标为2，其纵坐标为-2﹣2022×1＝﹣2024．
∴经过2021次变换后，正方形ABCD的顶点C的坐标为（2，﹣2024）．
故选：D．
【点睛】本题考查了坐标与图形变化﹣对称、规律型﹣点的坐标、坐标与图形变化﹣平移，解决本题的关键是掌握对称性质和平移的性质．
24. （2022洛阳二模）如图，在平面直角坐标系中，直线为正比例函数的图象，点的坐标为，过点作轴的垂线交直线于点，以为边作正方形；过点作直线的垂线，垂足为，交轴于点，以为边作正方形；过点作轴的垂线，垂足为，交直线于点，以为边作正方形，…，按此规律操作下所得到的正方形的面积是（ ）

A. B. C. D.
【答案】B
【解析】
【分析】由已知，直线l是第一、三象限的角平分线，结合A1（1，0），根据勾股定理求出每个正方形的边长，可分别求出正方形、正方形、正方形的面积，从中发现规律．
【详解】解：∵直线l为函数y=x的图象，
∴
∴．
∴正方形的面积为1；
由勾股定理得，
∴
∴正方形的面积为：
同理可得，
∴正方形的面积为：；…
∵第1个正方形的面积为1=，第2个正方形的面积为，第3个正方形的面积为，…，
∴第n个正方形的面积为：．
故选：B
【点睛】本题考查了勾股定理、正方形的性质、正比例函数的图象和性质、探索规律等知识点，运用正比例函数的性质是解题的基础，运用勾股定理求每个正方形的边长是关键．
25. （2022开封一模）如图，在平面直角坐标系中，将正方形OABC绕点O顺时针旋转45°后得到正方形，依此方式，绕点O连续旋转2022次得到正方形，如果点C的坐标为，那么点的坐标为（ ）

A. B. C. D.
【答案】B
【解析】
【分析】由正方形的性质和旋转的性质探究规律，利用规律解决问题即可．
【详解】解：如图

∵四边形OA1BC1是正方形，，



将正方形OABC绕点O顺时针旋转45°后得到正方形，

∵每次旋转45°
360°÷45°=8，8次一循环
∵2022÷8=252⋅⋅⋅6
点的坐标与点B5重合
即B2022与B1关于O对称

故选B
【点睛】本题考查了正方形的性质、旋转的性质、坐标与图形的变化、规律型：点的坐标等知识，解题的关键是学会从特殊到一般的探究规律的方法
26. （2022焦作二模）在平面直角坐标系中，等边如图放置，点A的坐标为，每一次将绕着点O逆时针方向旋转60°，同时每边扩大为原来的2倍，第一次旋转后得到，第二次旋转后得到，…，依次类推，则点的坐标为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】分别求出旋转后点A的对应点的位置及到原点O的长度，发现规律：如此循环，每旋转6次，A的对应点又回到x轴正半轴，由此得到答案．
【详解】解：由已知可得：
第一次旋转后，点A1在第一象限，OA1=22，
第二次旋转后，点A2在第二象限，OA2=23，
第三次旋转后，点A3在x轴负半轴，OA3=24，
第四次旋转后，点A4第三象限，OA4=25，
第五次旋转后，点A5在第四象限，OA5=26，
第六次旋转后，点A6在x轴正半轴，OA6=27，
如此循环，每旋转6次，A的对应点又回到x轴正半轴，而，
∴点x轴正半轴，且OA2022=22023，
∴点的坐标为，
故选：C．
【点睛】此题考查了坐标的规律计算，正确计算发现规律并运用规律解决问题是解题的关键．
27.（2022河南二模） 如图，在中，顶点A在x轴的负半轴上，，，，将绕点A逆时针旋转，每秒旋转90°，则第2022秒旋转结束时，点B的坐标为（ ）

A. B. C. D.
【答案】A
【解析】
【分析】每秒旋转90°，每4秒旋转1周，第2022秒旋转结束时与第2秒旋转结束时的位置相同，与△ABC关于点A成中心对称，求出点A的坐标，即可求得结论．
【详解】解：2022除以4等于505，余数为2，
∴第2022秒旋转结束时与第2秒旋转结束时的位置相同，
∵，，
∴OB=2，BC=，
∵∠AOB=90°，
∴，
∴A(-1,0),
∵，，
∴绕点A逆时针旋转2022秒旋转结束时，点B的坐标为（-2，-2）．
故选：A．
【点睛】本题主要考查了规律旋转，中心对称，解决问题的关键是探究旋转规律，确定旋转最后位置，熟练掌握中心对称的性质解答．
28. （2022青海中考） 木材加工厂将一批木料按如图所示的规律依次摆放，则第个图中共有木料______根.

【答案】
【解析】
【分析】第一个图形有1根木料，第二个图形有根木料，第三个图形有根木料，第四个图形有根木料，以此类推，得到第个图形有根木料．
【详解】解：∵第一个图形有根木料，
第二个图形有根木料，
第三个图形有根木料，
第四个图形有木料，
∴第个图形有根木料，
故答案为：．
【点睛】本题考查了图形的变化类问题，仔细观察，分析，归纳并发现其中的规律是解本题的关键．
29. （2022德阳中考）古希腊的毕达哥拉斯学派对整数进行了深入的研究，尤其注意形与数的关系，“多边形数”也称为“形数”，就是形与数的结合物．用点排成的图形如下：其中：图①的点数叫做三角形数，从上至下第一个三角形数是1，第二个三角形数是，第三个三角形数是，……图②的点数叫做正方形数，从上至下第一个正方形数是1，第二个正方形数是，第三个正方形数是，……由此类推，图④中第五个正六边形数是______．

【答案】45
【解析】
【分析】根据题意找到图形规律，即可求解．
【详解】根据图形，规律如下表：

三角形
3
正方形
4
五边形
5
六边形
6

M边形
m
1
1
1
1
1

1
2
1+2
1+2
1
1+2
1
1
1+2
1
1
1

1+2

3
1+2+3
1+2+3
1+2


1+2+3
1+2
1+2
1+2+3
1+2
1+2
1+2

1+2+3

4
1+2+3+4
1+2+3+4
1+2+3
1+2+3+4
1+2+3
1+2+3
1+2+3+4
1+2+3
1+2+3
1+2+3

1+2+3+4








n










由上表可知第n个M边形数为：，
整理得：，
则有第5个正六边形中，n=5，m=6，代入可得：，
故答案为：45．
【点睛】本题考查了整式--图形类规律探索，理解题意是解答本题的关键．
30．（2022遂宁中考）（4分）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为 　127　．
【分析】由已知图形观察规律，即可得到第六代勾股树中正方形的个数．
【解答】解：∵第一代勾股树中正方形有1+2＝3（个），
第二代勾股树中正方形有1+2+22＝7（个），
第三代勾股树中正方形有1+2+22+23＝15（个），
.....．
∴第六代勾股树中正方形有1+2+22+23+24+25+26＝127（个），
故答案为：127．
【点评】本题考查图形中的规律问题，解题的关键是仔细观察图形，得到图形变化的规律．
31. （2022泰安中考） 观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n的值为____________．


【答案】不存在
【解析】
【分析】首先根据n=1、2、3、4时，“•”的个数分别是3、6、9、12，判断出第n个图形中“•”的个数是3n；然后根据n=1、2、3、4，“○”的个数分别是1、3、6、10，判断出第n个“○”的个数是；最后根据图形中的“○”的个数和“．”个数差为2022，列出方程，解方程即可求出n的值是多少即可．
【详解】解：∵n=1时，“•”的个数是3=3×1；
n=2时，“•”的个数是6=3×2；
n=3时，“•”的个数是9=3×3；
n=4时，“•”的个数是12=3×4；
……
∴第n个图形中“•”的个数是3n；
又∵n=1时，“○”的个数是1=；
n=2时，“○”的个数是，
n=3时，“○”的个数是，
n=4时，“○”的个数是，
……
∴第n个“○”的个数是，
由图形中的“○”的个数和“．”个数差为2022
①，②
解①得：无解
解②得：
故答案为：不存在
【点睛】本题考查了图形类规律，解一元二次方程，找到规律是解题的关键．
32. （2022十堰中考） 如图，某链条每节长为，每两节链条相连接部分重叠的圆的直径为，按这种连接方式，50节链条总长度为_________．

【答案】91
【解析】
【分析】通过观察图形可知，1节链条的长度是，2节链条的长度是（2.8×2-1），3节链条的长度是（2.8×3-1×2），n节链条的长度是2.8n-1×（n-1），据此解答即可求解．
【详解】解：2节链条的长度是（2.8×2-1），
3节链条的长度是（2.8×3-1×2），
n节链条的长度是2.8n-1×（n-1），
所以50节链条的长度是：2.8×50-1×（50-1）
=140-1×49
=91
故答案为：91
【点睛】此题考查的图形类规律，关键是找出规律，得出n节链条长度为2.5×n-0.8×（n-1）．
33. （2022广安中考）如图，四边形ABCD是边长为的正方形，曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的．其中，弧DA1的圆心为A，半径为AD；弧A1B1的圆心为B，半径为BA1；弧B1C1的圆心为C，半径为CB1；弧C1D1的圆心为D，半径为DC1…．弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A、B、C、D循环，则弧C2022D2022的长是___________（结果保留π）．

【答案】2022π
【解析】
【分析】根据题意有后一段弧的半径总比前一段弧的半径长，又因为的半径为，可知任何一段弧的半径都是的倍数，根据圆心以A、B、C、D四次一个循环，可得弧的半径为：，再根据弧长公式即可作答．
【详解】根据题意有：
的半径，
的半径，
的半径，
的半径，
的半径，
的半径，
的半径，
的半径，
．．．
以此类推可知，故弧的半径为：，
即弧的半径为：，
即弧的长度为：，
故答案为：．
【点睛】本题考查了弧长的计算公式，找到每段弧的半径变化规律是解答本题的关键．
34. （2022绥化中考） 如图，，点在射线上，且，过点作交射线于，在射线上截取，使；过点作交射线于，在射线上截取，使.按照此规律，线段的长为________．

【答案】
【解析】
【分析】解直角三角形分别求得，，，……，探究出规律，利用规律即可解决问题．
【详解】解：，
是直角三角形，
在中，，，
，
，，
，
，
，
，
，
同理可得：，，……，
，
，
故答案为：．
【点睛】本题考查了图形的规律，解直角三角形，平行线的判定，相似三角形的判定与性质，解题的关键是学会探究规律的方法．
35. （2022牡丹江中考） 下列图形是将等边三角形按一定规律排列，则第个图形中所以等边三角形的个数是__________．

【答案】485
【解析】
【详解】试题分析：观察图形，找出数字与图形之间的联系：
由图可以看出：第一个图形中5个正三角形，
第二个图形中5×3+2=17个正三角形，
第三个图形中17×3+2=53个正三角形，
由此得出第四个图形中53×3+2=161个正三角形，
第五个图形中161×3+2=485个正三角形．
考点：探索规律题（图形的变化类）．
36. （2022牡丹江中考） 如图所示，以O为端点画六条射线后OA，OB，OC，OD，OE，O后F，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，7，8…后，那么所描的第2013个点在射线___上．

【答案】OC
【解析】
【详解】试题分析：∵1在射线OA上，2在射线OB上，3在射线OC上，4在射线OD上，5在射线OE上，6在射线OF上，7在射线OA上，…
∴每六个一循环．
∵2013÷6=335…3，
∴所描的第2013个点在射线和3所在射线一样．
∴所描的第2013个点在射线OC上．
37.（2022大庆中考） 观察下列“蜂窝图”，按照这样的规律，则第16个图案中的“”的个数是____________．

【答案】49

【解析】
【分析】根据题意可知：第1个图案中有六边形图形：1+2+1=4个，第2个图案中有六边形图形：2+3+2=7个，……由规侓即可得答案．
【详解】解：∵第1个图案中有六边形图形：1+2+1=4个，
第2个图案中有六边形图形：2+3+2=7个，
第3个图案中有六边形图形：3+4+3=10个，
第4个图案中有六边形图形：4+5+4=13个，
……
∴第16个图案中有六边形图形：16+17+16=49个，
故答案为：49．
【点睛】此题考查图形的变化规律，解题的关键是找出图形之间的运算规律，利用规律解决问题．
38. （2022毕节中考） 如图，在平面直角坐标系中，把一个点从原点开始向上平移1个单位，再向右平移1个单位，得到点；把点向上平移2个单位，再向左平移2个单位，得到点；把点向下平移3个单位，再向左平移3个单位，得到点；把点向下平移4个单位，再向右平移4个单位，得到点；…；按此做法进行下去，则点的坐标为_________．


【答案】
【解析】
【分析】先根据平移规律得到第n次变换时，相当于把点的坐标向右或向左平移n个单位长度，再向右或向上平移n个单位长度得到下一个点，然后推出每四次坐标变换为一个循环，每一个循环里面横坐标不发生变化，纵坐标向下平移4个单位长度，从而求出点A8的坐标为（0，-8），由此求解即可．
【详解】解：∵把一个点从原点开始向上平移1个单位，再向右平移1个单位，得到点；把点向上平移2个单位，再向左平移2个单位，得到点；把点向下平移3个单位，再向左平移3个单位，得到点；把点向下平移4个单位，再向右平移4个单位，得到点，
∴第n次变换时，相当于把点的坐标向右或向左平移n个单位长度，再向右或向上平移n个单位长度得到下一个点，
∵O到A1是向右平移1个单位长度，向上平移1个单位长度，A1到A2是向左2个单位长度，向上平移2个单位长度，A2到A3是向左平移3个单位长度，向下平移3个单位长度，A3到A4是向右平移4个单位长度，向下平移4个单位长度，A4到A5是向右平移5个单位长度，向上平移5个单位长度，
∴可以看作每四次坐标变换为一个循环，每一个循环里面横坐标不发生变化，纵坐标向下平移4个单位长度，
∴点A8的坐标为（0，-8），
∴点A8到A9的平移方式与O到A1的方式相同（只指平移方向）即A8到A9向右平移9个单位，向上平移9个单位，
∴A9的坐标为（9，1），
同理A9到A10的平移方式与A1到A2的平移方式相同（只指平移方向），即A9到A10向左平移10个单位，向上平移10个单位，
∴A10的坐标为（-1，11），
故答案为：（-1，11）．
【点睛】本题主要考查了点的坐标规律探索，正确找到规律是解题的关键．
39．（2022鄂尔多斯中考）按一定规律排列的数据依次为，，，……按此规律排列，则第30个数是 　　．
【分析】由所给的数，发现规律为第n个数是，当n＝30时即可求解．
【解答】解：∵，，，……，
∴第n个数是，
当n＝30时，＝＝，
故答案为：．
【点评】本题考查数字的变化规律，能够通过所给的数，探索出数的一般规律是解题的关键．
40. （2022眉山中考） 将一组数，2，，，…，，按下列方式进行排列：
，2，，；
，，，4；
…
若2的位置记为，的位置记为，则的位置记为________．
【答案】
【解析】
【分析】先找出被开方数的规律，然后再求得的位置即可．
【详解】数字可以化成：
，，，；
，，，；
∴规律为：被开数为从2开始的偶数，每一行4个数，
∵，28是第14个偶数，而
∴的位置记为
故答案为：
【点睛】本题考查了类比点的坐标解决实际问题的能力和阅读理解能力．被开方数全部统一是关键．
41. （2022宿迁中考） 按规律排列的单项式：，，，，，…，则第20个单项式是_____．
【答案】
【解析】
【分析】观察一列单项式发现偶数个单项式的系数为：奇数个单项式的系数为：而单项式的指数是奇数，从而可得答案．
详解】解：，，，，，…，
由偶数个单项式的系数为： 所以第20个单项式的系数为
第1个指数为：
第2个指数为：
第3个指数为：

指数为
所以第20个单项式是：
故答案为：
【点睛】本题考查的是单项式的系数与次数的含义，数字的规律探究，掌握“从具体到一般的探究方法”是解本题的关键．
42. （2022舟山中考） 观察下面的等式：，，，……
（1）按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）
（2）请运用分式的有关知识，推理说明这个结论是正确的．
【答案】（1）
（2）见解析
【解析】
【分析】（1）根据所给式子发现规律，第一个式子的左边分母为2，第二个式子的左边分母为3，第三个式子的左边分母为4，…；右边第一个分数的分母为3，4，5，…，另一个分数的分母为前面两个分母的乘积；所有的分子均为1；所以第（n+1）个式子为．
（2）由（1）的规律发现第（n+1）个式子为，用分式的加法计算式子右边即可证明．
【小问1详解】
解：∵第一个式子，
第二个式子，
第三个式子，
……
∴第（n+1）个式子；
【小问2详解】
解：∵右边==左边，
∴．
【点睛】此题考查数字的变化规律，分式加法运算，解题关键是通过观察，分析、归纳发现其中各分母的变化规律．
43. （2022张家界中考）有一组数据：a1=31×2×3，a2=52×3×4，a3=73×4×5，…，an=2n+1n(n+1)(n+2).记Sn=a1+a2+a3+…+an，则S12=______．
14.【答案】201182 
【解析】解：a1=31×2×3=12=12×1+12−32×11+2；
a2=52×3×4=524=12×12+11+2−32×12+2；
a3=73×4×5=760=12×13+13+1−32×13+2；
…，
an=2n+1n(n+1)(n+2)=12×1n+1n+1−32×1n+2，
当n=12时，
原式=12(1+12+13+...+112)+(12+13+...+113)−32×(13+14+...+114)
=201182，
故答案为：201182．
通过探索数字变化的规律进行分析计算．
本题考查分式的运算，探索数字变化的规律是解题关键．
44. （2022达州中考）人们把这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设，，记，，…，，则_______．
【答案】5050
【解析】
【分析】利用分式的加减法则分别可求S1=1，S2=2，S100=100，•••，利用规律求解即可．
【详解】解：，，
，
，
，
…，


故答案为：5050
【点睛】本题考查了分式的加减法，二次根式的混合运算，求得，找出的规律是本题的关键．
45. （2022怀化中考） 正偶数2，4，6，8，10，…，按如下规律排列，

则第27行的第21个数是 _____．
【答案】744
【解析】
【分析】由题意知，第n行有n个数，第n行的最后一个偶数为n（n+1），计算出第27行最后一个偶数，再减去与第21位之差即可得到答案．
【详解】由题意知，第n行有n个数，第n行的最后一个偶数为n（n+1），
∴第27行的最后一个数，即第27个数为，
∴第27行的第21个数与第27个数差6位数，即，
故答案为：744．
【点睛】本题考查数字类规律的探究，根据已知条件的数字排列找到规律，用含n的代数式表示出来由此解决问题是解题的关键
46. （2022恩施中考）观察下列一组数：2，，，…，它们按一定规律排列，第n个数记为，且满足．则________，________．
【答案】 ①. ②.
【解析】
【分析】由已知推出，得到，，，，上述式子相加求解即可．
【详解】解：∵；∴，
∵，
∵，
∴a4=，
∴，，，
把上述2022-1个式子相加得，
∴a2022=，
故答案为：，．
【点睛】此题主要考查了数字的变化规律，关键是得出，利用裂项相加法求解．
47.（2022盐城中考）《庄子⋅天下篇》记载“一尺之棰，日取其半，万世不竭”.如图，直线l1：y=12x+1与y轴交于点A，过点A作x轴的平行线交直线l2：y=x于点O1，过点O1作y轴的平行线交直线l1于点A1，以此类推，令OA=a1，O1A1=a2，…，On−1An−1=an，若a1+a2+…+an≤S对任意大于1的整数n恒成立，则S的最小值为______．



16.【答案】32 
【解析】解：把x=0代入y=12x+1得，y=1，
∴A(0,1)，
∴OA=a1=1，
把y=1代入y=x得，x=1，
∴O1(1,1)，
把x=1代入y=12x+1得，y=12×1+1=32，
∴A1(1,32)，
∴O1A1=a2=32−1=12，
把y=32代入y=x得，y=32，
∴O2(32,32)，
把x=32代入y=12x+1得，y=12×32+1=74，
∴A2(32,74)，
∴O2A2=a3=74−32=14，
…，
∴On−1An−1=an=(12)n−1，
∵a1+a2+…+an≤S对任意大于1的整数n恒成立，
∴n=2时，S的值最小，
∵S≥a1+a2=1+12=32，
∴S的最小值为32，
故答案为：32．
由直线l1的解析式求得A，即可求得a1，把A的坐标代入y=x求得O1的坐标，进而求得A1的坐标，即可求得a2，把A1的纵坐标代入y=x求得O2的坐标，进而求得A2的坐标，即可求得a3，…，得到规律，即可求得On−1An−1=an=(12)n−1，根据a1+a2+…+an≤S对任意大于1的整数n恒成立，则S的最小值为n=2时的最小值．
本题考查了一次函数图象上点的坐标特征，图象上点的坐标适合函数的解析式是解题的关键．
48. （2022龙东中考） 如图，在平面直角坐标系中，点，，，……在x轴上且，，，……按此规律，过点，，，……作x轴的垂线分别与直线交于点，，，……记，，，……的面积分别为，，，……，则______．

【答案】
【解析】
【分析】先求出，可得，再根据题意可得，从而得到∽∽∽……∽，再利用相似三角形的性质，可得∶∶∶……∶= ，即可求解．
【详解】解：当x=1时，，
∴点，
∴，
∴，
∵根据题意得：，
∴∽∽∽……∽，
∴∶∶∶……∶= OA12∶OA22∶OA32……∶OAn2，
∵，，，……，
∴，，……，
∴∶∶∶……∶= ，
∴，
∴．
故答案为：．
【点睛】本题主要考查了图形与坐标的规律题，相似三角形的判定和性质，明确题意，准确得到规律，是解题的关键．
49．（2022荆门中考）如图，过原点的两条直线分别为l1：y＝2x，l2：y＝﹣x，过点A（1，0）作x轴的垂线与l1交于点A1，过点A1作y轴的垂线与l2交于点A2，过点A2作x轴的垂线与l1交于点A3，过点A3作y轴的垂线与l2交于点A4，过点A4作x轴的垂线与l1交于点A5，⋯，依次进行下去，则点A20的坐标为 　（32，﹣32）　．

【分析】写根据一次函数图象上点的坐标特征可得出点A1、A2、A3、A4、A5、A6、A7、A8等的坐标，根据坐标的变化即可找出变化规律“A4n+1（22n，22n+1），A4n+2（﹣22n+1，22n+1），A4n+3（﹣22n+1，﹣22n+2），A4n+4（22n+2，﹣22n+2）（n为自然数）”，依此规律结合20＝5×4即可找出点A20的坐标．
【解答】解：当x＝1时，y＝2，
∴点A1的坐标为（1，2）；
当y＝﹣x＝2时，x＝﹣2，
∴点A2的坐标为（﹣2，2）；
同理可得：A3（﹣2，﹣4），A4（4，﹣4），A5（4，8），A6（﹣8，8），A7（﹣8，﹣16），A8（16，﹣16），A9（16，32），…，
∴A4n+1（22n，22n+1），A4n+2（﹣22n+1，22n+1），
A4n+3（﹣22n+1，﹣22n+2），A4n+4（22n+2，﹣22n+2）（n为自然数）．
∵20＝5×4，
∴点A20的坐标为（22+2，﹣22+2），即（32，﹣32）．
故答案为：（32，﹣32）．
【点评】本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及规律型中点的坐标，根据坐标的变化找出变化规律“A4n+1（22n，22n+1），A4n+2（﹣22n+1，22n+1），A4n+3（﹣22n+1，﹣22n+2），A4n+4（22n+2，﹣22n+2）（n为自然数）”是解题的关键．
50. （2022齐齐哈尔中考）如图，直线与轴相交于点，与轴相交于点，过点作交轴于点，过点作轴交于点，过点作交轴于点，过点作轴交于点…，按照如此规律操作下去，则点的纵坐标是______________．

【答案】
【解析】
【分析】先根据30°的特殊直角三角形，如，，，求出B点，B1点的纵坐标，发现规律，即可
【详解】∵
当时，
当时，
故，
∴为30°的直角三角形
∴
∵
∴为30°的直角三角形
∴
∴为30°的直角三角形

∵轴
∴
∴
为30°的直角三角形

同理：


…

故：
故答案为：
【点睛】本题考查30°的特殊直角三角形；注意只用求点的纵坐标，即长度
51. （2022苏州中学三模）将边长为1的正方形纸片按如图所示方法进行对折，第1次对折后得到的图形面积为S1，第2次对折后得到的图形面积为S2，…，第n次对折后得到的图形面积为Sn，S1+S2+S3+…Sn=______（用含n的代数式表示）．

【答案】
【解析】
【分析】根据题意，先写出前面几个对折后的图形的面积，探究隐含规律，然后再求所得式子的值．
【详解】解：由题意可得：
S1=，
S2==，
S3=，
⋯，
Sn=，
∴S1+S2+S3+⋯+Sn=++⋯+，
令M=++⋯+，
则2M=1+++⋯+，
∴2M-M=1-，
即M=1-．
故答案为：1-．
【点睛】本题考查了图形的变化，解答本题的关键是明确题意，表示出每部分的图形面积，发现所得式子的规律特点，用错位相减法得到答案．
52. （2022山西侯马二模）如图是一组有规律的图案，它们都是由大小相同的组成的，第1个图案中有5个，第2个图案中有8个，第3个图案中有11个……按此规律，第n个图案中有______个．（用含n的代数式表示）

【答案】##（2+3n）
【解析】
【分析】根据图案找出规律即可；
【详解】解：第一个：5=3×1+2，
第二个：8=3×2+2，
第三个：9=3×3+2，
∴第n个图案中有个；
故答案为：（3n+2）.
【点睛】本题主要考查列代数式，根据图案规律，写出第n个图案中图形个数是解题的关键．
53.（2022太原二模） 如图是一组有规律的图案，它们是由相同的正方形和相同的圆组成的，正方形涂有阴影，依此规律，则第n个图案中有______个圆．（用含有n的代数式表示）

【答案】
【解析】
【分析】观察不难发现，后一个图案比前一个图案多3个圆，然后写出第n个图案的圆的个数即可．
【详解】解：由图可得，第1个图案有圆的个数为4=3×1+1，
第2个图案有圆的个数为7=3×2+1，
第3个图案有圆的个数为9=4×2+1，
…...
第n个图案有圆的个数为3n+1．
故答案为：（3n+1）．
【点睛】本题是对图形变化规律的考查，观察出“后一个图案比前一个图案多3个圆”是解题的关键．
54. （2022大同二模）将大小相同的小圆按如图所示的规律摆放：第1个图形有5个小圆，第2个图形有8个小圆，第3个图形有11个小圆，…依此规律，第n个图形的小圆个数是___________个．


【答案】##（2+3n）
【解析】
【分析】根据图形的变化寻找规律即可求解．
【详解】解：观察图形的变化可知：
第1个图形有1×3+2=5个小圆，
第2个图形有2×3+2=8个小圆，
第3个图形有3×3+2=11个小圆，
…，
发现规律：
第n个图形的小圆个数是3n +2．
故答案为：(3n+2)．
【点睛】本题考查了规律型-图形的变化，解决本题的关键是观察图形的变化寻找规律并总结规律，会利用找到的规律进行解题．
55. （2022北京朝阳区一模）如图，2022年北京冬奥会上，一些可看作正六边形的“小雪花”对称地排列在主火炬周围，中间空出了13个“小雪花”的位置来突出主火炬，在其中91个“小雪花”上面写有此次参会的国家或地区的名称，此外还有几个“小雪花”上面只有中国结图案，这些只有中国结图案的“小雪花”共有_________个．

【答案】5
【解析】
【分析】根据图形先计算图中共有的小雪花的数量，再减去上面写有此次参会的国家或地区名称的小雪花，即可得答案．
【详解】解：仔细观察图像可知，图中共有小雪花
3×2+4×2+4×2+9×2+10×2＋9×2+6×2+3×2=96（个）
其中有在其中91个“小雪花”上面写有此次参会的国家或地区的名称，
∴“小雪花”上面只有中国结图案有 96-91=5（个）
故答案为：5．
【点睛】本题考查了图形的规律，以及有理数的加减运算，解题的关键是仔细看图．
56.（2022西工大附中三模） 1261年我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律，我们把这个三角形称为“杨辉三角”，请观察图中的数字排列规律，求a+2b﹣c的值为_____．

【答案】16
【解析】
【分析】根据题目中的数据可知，a、b、c分别为上一行中左上角和右上角的数字之和，从而可以求得所求式子的值．
【详解】解：由图可得，
a＝1+5＝6，b＝5+10＝15，c＝10+10＝20，
∴a+2b﹣c＝6+2×15﹣20＝16，
故答案为：16．
【点睛】本题考查数字的变化类，解答本题的关键是明确题意，发现题目中数字的变化规律，求出a、b、c的值．
57. （2022运城二模）一组按规律排列的式子，，，，…，则第n个式子是_____．
【答案】或
【解析】
【分析】从已知单项式的字母指数出发寻找其与序数间的关系，从而得出答案．
【详解】解：∵第1个单项式 ，
第2个单项式，
第3个单项式，
第4个单项式，
……
∴第n（n为正整数）个单项式为，即．
故答案为：或．
【点睛】本题主要考查单项式字母指数的变化规律，解题的关键是根据已知单项式，从字母指数入手寻找其与序数间的关系．
58. （2022临汾二模）观察下列各项：，，，，…，则第项是______________．
【12题答案】
【答案】
【解析】
【分析】根据已知可得出规律：第一项：，第二项：，第三项：…即可得出结果．
【详解】解：根据题意可知：
第一项：，
第二项：，
第三项：，
第四项：，
…
则第项是；
故答案为：．
【点睛】此题属于数字类规律问题，根据已知各项的规律得出结论是解决此类题目的关键．
59. （2022北京房山二模）为确定传染病的感染者，医学上可采用“二分检测方案”．假设待检测的总人数是（为正整数）．将这个人的样本混合在一起做第1轮检测（检测1次），如果检测结果是阴性，可确定这些人都未感染；如果检测结果是阳性，可确实其中感染者，则将这些人平均分成两组，每组个人的样本混合在一起做第2轮检测，每组检测1次．依此类推：每轮检测后，排除结果为阴性的组，而将每个结果为阳性的组再平均分成两组，做下轮检测，直至确定所有的感染者．
例如，当待检测的总人数为8，且标记为“”的人是唯一感染者时，“二分检测方案”可用如图所示．从图中可以看出，需要经过4轮共次检测后，才能确定标记为“”的人是唯一感染者．

（1）的值为___________；
（2）若待检测的总人数为8，采用“二分检测方案”，经过4轮共9次检测后确定了所有的感染者，写出感染者人数的所有可能值___________；
【答案】（1）7 （2）2、3、4
【解析】
【分析】（1）由图可计算得到n的取值．
（2）当经过4轮共9次检测后确定所有感染者，只需第3轮对两组都进行检查，由此得到所有可能的结果．
【小问1详解】
由题意可知，第1轮需检测1次，第2轮需检测2次，第3轮需检测2次，第4轮需检测2次，
∴
故答案为7．
【小问2详解】
由（1）可知，若只有1个感染者，则只需7次检测即可，经过4轮9次检测查出所有感染者，比只有1个感染者多2次检测，则只需第3轮时，对两组都进行检查，即对最后四个人进行检查，可能的结果如下图所示：
故答案为：2、3、4

【点睛】本题考查了数学建模能力，正确理解题意并合理建模是解答本题的关键．