资料中包含下列文件,点击文件名可预览资料内容












还剩52页未读,
继续阅读
所属成套资源:高中数学同步课件选择性必修第一册课件+讲义(新教材)
成套系列资料,整套一键下载
高中数学新教材选择性必修第一册课件+讲义 第2章 §2.5 2.5.1 第1课时 直线与圆的位置关系
展开
这是一份高中数学新教材选择性必修第一册课件+讲义 第2章 §2.5 2.5.1 第1课时 直线与圆的位置关系,文件包含高中数学新教材选择性必修第一册第2章§25251第1课时直线与圆的位置关系pptx、高中数学新教材选择性必修第一册第2章§25251第1课时直线与圆的位置关系教师版docx、高中数学新教材选择性必修第一册第2章§25251第1课时直线与圆的位置关系学生版docx等3份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
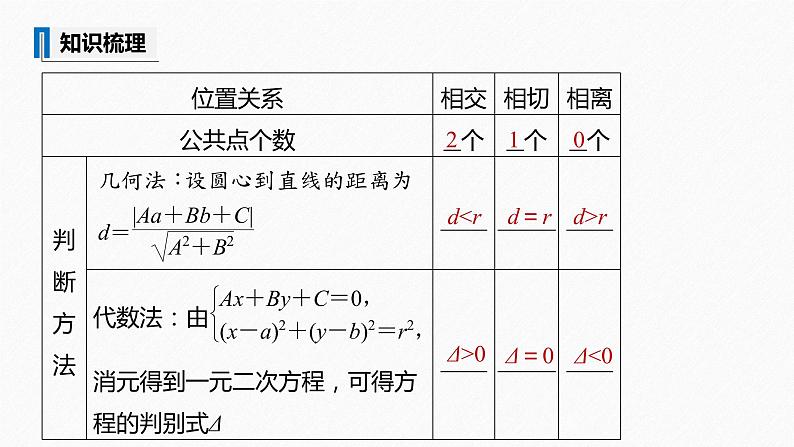
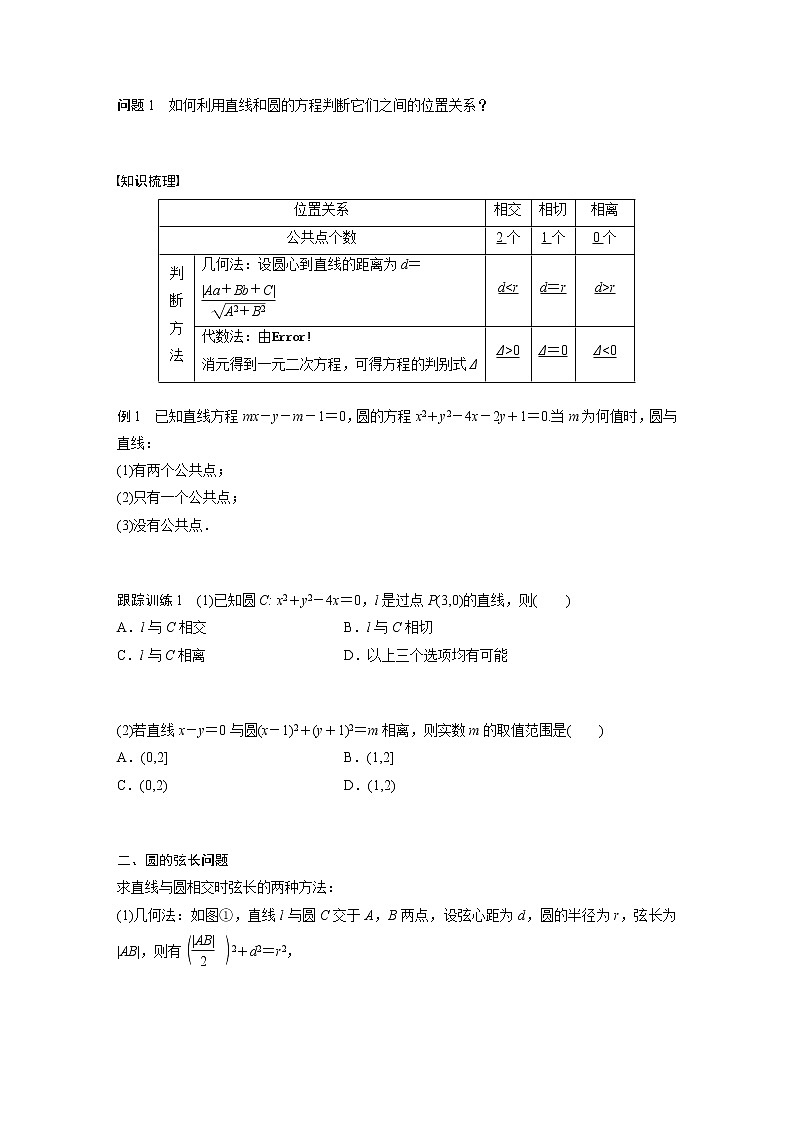
第1课时 直线与圆的位置关系第二章 2.5.1 直线与圆的位置关系1.掌握直线与圆的三种位置关系:相交、相切、相离.2.会用代数法和几何法来判断直线与圆的三种位置关系.学习目标海上日出是非常壮丽的美景.在海天交于一线的天际,一轮红日慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着斑斓的霞光和迷人的风采.在这个过程中,把太阳看作一个圆,海天交线看作一条直线,日出的过程中也体现了直线与圆的位置关系.导语随堂演练课时对点练一、直线与圆的位置关系的判断二、圆的弦长问题三、求圆的切线方程内容索引一、直线与圆的位置关系的判断问题1 如何利用直线和圆的方程判断它们之间的位置关系?提示 转化为它们的方程组成的方程组有无实数解、有几个实数解.210drΔ>0Δ=0Δ<0例1 已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,圆与直线:(1)有两个公共点;(2)只有一个公共点;(3)没有公共点.解 方法一 将直线mx-y-m-1=0代入圆的方程化简整理得,(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.则Δ=4m(3m+4).方法二 已知圆的方程可化为(x-2)2+(y-1)2=4,即圆心为C(2,1),半径r=2.圆心C(2,1)到直线mx-y-m-1=0的距离反思感悟 直线与圆的位置关系的判断方法(1)几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.(2)代数法:根据直线方程与圆的方程组成的方程组的解的个数来判断.(3)直线系法:若直线恒过定点,可通过判断定点与圆的位置关系来判断直线与圆的位置关系.但有一定的局限性,必须是过定点的直线系.跟踪训练1 (1)已知圆C: x2+y2-4x=0,l是过点P(3,0)的直线,则A.l与C相交 B.l与C相切C.l与C相离 D.以上三个选项均有可能√解析 将点P(3,0)代入圆的方程,得32+02-4×3=9-12=-3<0,∴点P(3,0)在圆内.∴过点P的直线l必与圆C相交.(2)若直线x-y=0与圆(x-1)2+(y+1)2=m相离,则实数m的取值范围是A.(0,2] B.(1,2]C.(0,2) D.(1,2)√∴m<2,∵m>0,∴00),解得a=-6(舍)或a=2,则圆C的标准方程为(x-2)2+y2=2.(2)已知过点P(1,3)的直线l交圆C于A,B两点,且|AB|=2,求直线l的方程.12345678910111213141516若斜率存在,设直线方程为y-3=k(x-1),即kx-y-k+3=0.11.已知圆C与直线x+y+3=0相切,直线mx+y+1=0始终平分圆C的面积,则圆C的方程为A.x2+y2-2y=2 B.x2+y2+2y=2C.x2+y2-2y=1 D.x2+y2+2y=1√12345678910111213141516综合运用解析 在直线mx+y+1=0的方程中,令x=0,则y=-1,则直线mx+y+1=0过定点(0,-1).由于直线mx+y+1=0始终平分圆C的面积,则点(0,-1)是圆C的圆心,又圆C与直线x+y+3=0相切,12345678910111213141516因此,圆C的方程为x2+(y+1)2=2,即x2+y2+2y=1.A.4x+3y-13=0 B.3x+4y-15=0C.3x+4y+15=0 D.x=1√12345678910111213141516√解析 由题意知圆心C的坐标为(2,0),半径为r=2,12345678910111213141516当直线l的斜率存在时,设直线l的方程为y-3=k(x-1),即kx-y-k+3=0,12345678910111213141516即4x+3y-13=0.12345678910111213141516√解析 圆的标准方程为(x+1)2+(y-2)2=4,圆心为C(-1,2),半径为r=2,直线被圆截得的弦长为4,则圆心在直线上,所以-2m-2n=-2,m+n=1.又m>0,n>0,1234567891011121314151614.在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为________.12345678910111213141516设点F为其圆心,坐标为(1,3).√拓广探究12345678910111213141516故曲线并非表示整个单位圆,仅仅是单位圆在y轴右侧(含与y轴的交点)的部分.1234567891011121314151616.已知圆C的圆心在x轴的正半轴上,半径为2.且被直线l:4x-3y-3=0截得的弦长为(1)求圆C的方程;12345678910111213141516∴圆C的方程为(x-2)2+y2=4.(2)设P是直线x+y+4=0上的动点,过点P作圆C的切线PA,切点为A,证明:经过A,P,C三点的圆必过定点,并求所有定点的坐标.12345678910111213141516解 ∵P是直线x+y+4=0上一点.设P(m,-m-4),∵PA为圆C的切线,∴PA⊥AC,即过A,P,C三点的圆是以PC为直径的圆.设圆上任一点Q(x,y),12345678910111213141516即x2+y2-2x+4y+m(-x+y+2)=0,12345678910111213141516∴经过A,P,C三点的圆必过定点(-1,-3)和(2,0).
第1课时 直线与圆的位置关系第二章 2.5.1 直线与圆的位置关系1.掌握直线与圆的三种位置关系:相交、相切、相离.2.会用代数法和几何法来判断直线与圆的三种位置关系.学习目标海上日出是非常壮丽的美景.在海天交于一线的天际,一轮红日慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着斑斓的霞光和迷人的风采.在这个过程中,把太阳看作一个圆,海天交线看作一条直线,日出的过程中也体现了直线与圆的位置关系.导语随堂演练课时对点练一、直线与圆的位置关系的判断二、圆的弦长问题三、求圆的切线方程内容索引一、直线与圆的位置关系的判断问题1 如何利用直线和圆的方程判断它们之间的位置关系?提示 转化为它们的方程组成的方程组有无实数解、有几个实数解.210d
相关资料
更多









