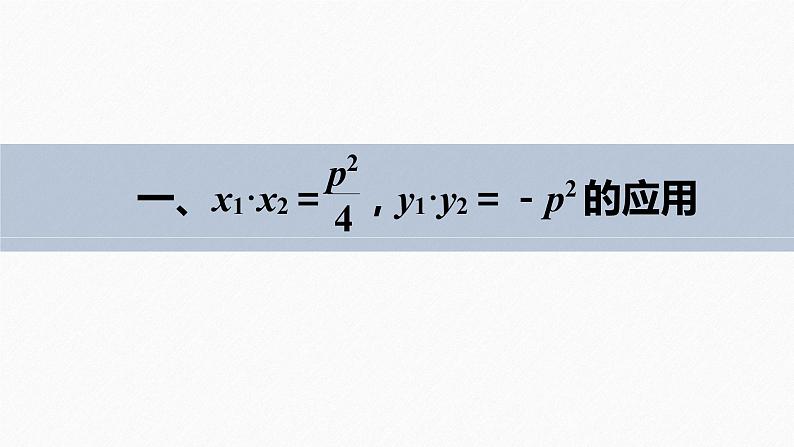
高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线优秀习题ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册3.3 抛物线优秀习题ppt课件，文件包含高中数学新教材选择性必修第一册第3章习题课抛物线焦点弦的应用pptx、高中数学新教材选择性必修第一册第3章习题课抛物线焦点弦的应用教师版docx、高中数学新教材选择性必修第一册第3章习题课抛物线焦点弦的应用学生版docx等3份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

高考政策|高中“新”课程，新在哪里?
1、科目变化：外语语种增加，体育与健康必修。第一，必修课程，由国家根据学生全面发展需要设置，所有学生必须全部修习、全部考试。第二，选择性必修课程，由国家根据学生个性发展和升学考试需要设置。第三，选修课程，由学校根据实际情况统筹规划开设，学生自主选择修习。2、课程类别变化，必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下，对原必修课程学分进行重构，由必修课程学分、选择性必修课程学分组成，适当增加选修课程学分。3、学时和学分变化，高中生全年假期缩减到11周。4、授课方式变化，选课制度将全面推开。5、考试方式变化，高考统考科目由教育部命题，学业水平合格性、等级性考试由各省命题。
习题课　抛物线焦点弦的应用
第三章　 圆锥曲线的方程
1.抛物线焦点弦的推导.2.利用抛物线的焦点弦求解弦长问题.
在上节中，我们已经掌握了抛物线焦点弦的一些性质：设AB是过抛物线y2＝2px(p>0)焦点F的弦，若A(x1，y1)，B(x2，y2)，则
(2)以弦AB为直径的圆与准线相切；
四、以弦AB为直径的圆与准线相切的应用
A.x2＝8y B.x2＝4yC.y2＝8x D.y2＝4x
设A(x1，y1)，B(x2，y2)，
得p＝4(舍负)，即抛物线C的方程为y2＝8x.
反思感悟　通过抛物线的特殊性质，脱离于传统的联立方程组求解，较为迅速的得到结果.
跟踪训练1　过抛物线y2＝2px(p>0)的焦点作一条直线交抛物线于点A(x1，y1)，B(x2，y2)，则 ＝____.
将直线AB的方程与抛物线的方程联立，
消去x得y2－2mpy－p2＝0，由根与系数的关系得y1y2＝－p2.由于点A，B均在抛物线上，
例2　抛物线的顶点在原点，以x轴为对称轴，经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8，试求抛物线的方程.
解　依题意可设抛物线的方程为y2＝2px(p>0)，
设直线交抛物线于A(x1，y1)，B(x2，y2)两点，
故所求的抛物线方程为y2＝4x.当抛物线方程设为y2＝－2px(p>0)时，同理可求得抛物线方程为y2＝－4x.综上，抛物线方程为y2＝±4x.
跟踪训练2　经过抛物线C：y2＝2px(p＞0)的焦点F，倾斜角为30°的直线l与C交于A，B两点，若线段AB的中点M的横坐标为7，那么p＝_____.
解析　 设A(x1，y1)，B(x2，y2)，∵AB的中点M的横坐标为7，∴x1＋x2＝14，
例3　过抛物线y2＝4x的焦点F的直线l与抛物线交于A，B两点，若|AF|＝2|BF|，则|AB|等于
反思感悟　将求弦长问题通过焦半径与p之间的关系，转化为焦半径问题.
跟踪训练3　如图，过抛物线y2＝2px(p>0)的焦点F的直线交抛物线于点A，B，交其准线l于点C，若F是AC的中点，且|AF|＝4，则线段AB的长为
例4　抛物线y2＝2px(p>0)的焦点为F，M为抛物线上一点.若△OFM的外接圆与抛物线的准线相切(O为坐标原点)，且外接圆的面积为9π，则p等于A.2 B.4 C.6 D.8
解析　∵△OFM的外接圆与抛物线的准线相切，∴△OFM的外接圆的圆心到准线的距离等于圆的半径.∵外接圆的面积为9π，∴外接圆的半径为3.
反思感悟　把焦点三角形的外接圆转化为以弦AB为直径的圆与准线相切，进行问题的求解.
跟踪训练4　已知抛物线x2＝2py(p>0)，直线l过它的焦点F，且与抛物线交于A，B两点，则以AB为直径的圆与抛物线的准线的位置关系是A.相离 B.相切C.相交 D.与p的取值有关
1.知识清单：抛物线焦点弦性质的应用.2.方法归纳：转化法.3.常见误区：对焦点弦的性质记忆混淆，导致出错.
解析　由题意可得抛物线的标准形式为x2＝8y，所以准线方程为y＝－2，
所以弦长|AB|＝5＋4＝9.
2.过抛物线C：y2＝8x的焦点F的直线交抛物线C于A，B两点，若|AF|＝6，则|BF|等于A.9或6 B.6或3 C.9 D.3
解析　方法一　设点A为第一象限内的点，设点A(x1，y1)，B(x2，y2)，则x1>0，y1>0，则由题意可得F(2,0)，|AF|＝x1＋2＝6，
将直线AB的方程代入y2＝8x化简得x2－5x＋4＝0，所以x2＝1，所以|BF|＝x2＋2＝3.
3.过抛物线y2＝8x的焦点作直线l交抛物线于A，B两点，若线段AB的中点的横坐标为3，则|AB|＝_____.
解析　由题意知抛物线y2＝8x的焦点为F(2,0)，p＝4，设A，B两点坐标分别为A(x1，y1)，B(x2，y2)，
∴x1＋x2＝6，抛物线的焦点弦|AB|＝x1＋x2＋p＝10.
4.过抛物线y2＝4x的焦点作直线交抛物线于P(x1，y1)，Q(x2，y2)两点，若x1＋x2＝6，则PQ中点M到抛物线准线的距离为____.
解析　由抛物线的方程y2＝4x，可得p＝2，故它的焦点F(1,0)，准线方程为x＝－1.
1.已知抛物线y2＝2px(p>0)的焦点弦的两端点分别为A(x1，y1)，B(x2，y2)，则 的值一定等于A.－4 D.－p2
2.已知AB是过抛物线2x2＝y的焦点的弦.若|AB|＝4，则AB中点的纵坐标是
解析　如图所示，设线段AB的中点为P(x0，y0)，分别过A，P，B三点作准线l的垂线，垂足分别为A′，Q，B′，
4.已知F为抛物线C：y2＝6x的焦点，过点F的直线l与C相交于A，B两点，且|AF|＝3|BF|，则|AB|等于A.6 B.8 C.10 D.12
解析　∵|AF|＝3|BF|，且p＝3，
∴|BF|＝2，|AF|＝6，∴|AB|＝|AF|＋|BF|＝8.
5.已知抛物线y2＝2px(p>0)的焦点为F，过点F的直线交抛物线于A，B两点，若|AF|＝4，|BF|＝1，则p等于
由|AF|＝4，|BF|＝1，
6.(多选)已知抛物线y2＝2px(p>0)，过抛物线的焦点F作直线与抛物线交于两点A(x1，y1)，B(x2，y2)，且抛物线的准线与x轴的交点为M，则以下结论正确的是
解析　由抛物线焦点弦的性质知ABD正确.
解析　设A(x1，y1)，B(x2，y2)，x1将直线方程与抛物线方程联立，
所以k2＝24，方程①即12x2－13x＋3＝0，
8.已知直线l：y＝x－1经过抛物线C：y2＝2px(p>0)的焦点，且与抛物线C交于A，B两点，则|AB|＝___.
由题意知，直线l：y＝x－1过点(1,0)，
9.已知直线l经过抛物线y2＝6x的焦点F，且与抛物线相交于A，B两点.(1)若直线l的倾斜角为60°，求|AB|的值；
解　方法一　因为直线l的倾斜角为60°，
若设A(x1，y1)，B(x2，y2).则x1＋x2＝5，
所以|AB|＝5＋3＝8.方法二　因为抛物线y2＝6x，所以p＝3，又直线l的倾斜角α＝60°，
(2)若|AB|＝9，求线段AB的中点M到准线的距离.
解　设A(x1，y1)，B(x2，y2)，由抛物线定义知，
10.已知点P(1，m)是抛物线C：y2＝2px(p>0)上的点，F为抛物线的焦点，且|PF|＝2，过焦点F的直线l与抛物线C相交于不同的两点A，B.(1)求抛物线C的方程；
∴抛物线方程为y2＝4x.
(2)若|AB|＝8，求直线l的斜率.
解　方法一　由(1)知焦点为F(1,0)，若直线l斜率不存在，则|AB|＝4，不合题意，因此设直线l的方程为y＝k(x－1)(k≠0)，
解得k＝1或k＝－1.
方法二　若直线l的斜率不存在，则|AB|＝4，不合题意，设直线l的倾斜角为α，
即α＝45°或135°，则k＝tan α＝±1.
11.(多选)已知抛物线C：y2＝4x的焦点为F，准线为l，过点F的直线与抛物线交于P(x1，y1)，Q(x2，y2)两点，点P在l上的射影为P1，则下列说法正确的是A.若x1＋x2＝6，则|PQ|＝8B.以PQ为直径的圆与准线l相切C.设M(0,1)，则|PM|＋|PP1|≥D.过点M(0,1)与抛物线C有且仅有一个公共点的直线至多有2条
解析　对于选项A，因为p＝2，所以x1＋x2＋2＝|PQ|，则|PQ|＝8，故A正确；对于选项B，由抛物线焦点弦的性质可知，B正确；对于选项C，因为F(1,0)，所以|PM|＋|PP1|＝|PM|＋|PF|≥|MF|＝ ，故C正确；对于选项D，显然直线x＝0，y＝1与抛物线只有一个公共点，设过M的直线方程为y＝kx＋1(k≠0)，
12.(多选)已知抛物线y2＝2px(p>0)上三点A(x1，y1)，B(1,2)，C(x2，y2)，F为抛物线的焦点，则下列说法正确的是A.抛物线的准线方程为x＝－1
C.若A，F，C三点共线，则y1y2＝－1D.若|AC|＝6，则AC的中点到y轴距离的最小值为2
解析　 把点B(1,2)代入抛物线y2＝2px，得p＝2，所以抛物线的准线方程为x＝－1，故A正确；
因为A，F，C三点共线，所以直线AC是焦点弦，所以y1y2＝－p2＝－4，故C不正确；
设AC的中点为M(x0，y0)，因为|AF|＋|CF|≥|AC|，|AF|＋|CF|＝x1＋1＋x2＋1＝2x0＋2，所以2x0＋2≥6，得x0≥2，即AC的中点到y轴距离的最小值为2，故D正确.
13.设F为抛物线C：y2＝3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为
14.过抛物线y2＝4x焦点F的直线交抛物线于A，B两点，交其准线于点C，且A，C位于x轴同侧.若|AC|＝2|AF|，则|BF|等于A.2 B.3 C.4 D.5
解析　抛物线y2＝4x的焦点F(1,0)，准线方程l：x＝－1，设准线l与x轴交于点H，不妨设点A在第四象限，过A和B分别作AD⊥l，BE⊥l，垂足分别为D，E，如图，由抛物线的定义可知|AF|＝|AD|，|BF|＝|BE|，又|AC|＝2|AF|，
15.(多选)已知点F是抛物线y2＝2px(p>0)的焦点，AB，CD是经过点F的弦且AB⊥CD，AB的斜率为k，且k>0，C，B两点在x轴上方，则下列结论中正确的是
A(x1，y1)，B(x2，y2)，直线AB的倾斜角为θ(θ≠0)，
设C(x3，y3)，D(x4，y4)，
故其最小值为8p2，故错误；
16.已知抛物线C的顶点为原点，焦点F与圆x2＋y2－2x＝0的圆心重合.(1)求抛物线C的标准方程；
解　由已知易得F(1,0)，则所求抛物线C的标准方程为y2＝4x.
(2)设定点A(3,2)，当P点在C上何处时，|PA|＋|PF|的值最小，并求最小值及点P的坐标；
解　设点P在抛物线C的准线上的射影为点B，根据抛物线定义知|PF|＝|PB|，要使|PA|＋|PF|的值最小，必P，A，B三点共线. 可得P(x1，2)，22＝4x1⇒x1＝1，即P(1,2).此时|PA|＋|PF|＝2＋2＝4.