沪科版八年级上册第14章 全等三角形14.2 三角形全等的判定优秀课件ppt

这是一份沪科版八年级上册第14章 全等三角形14.2 三角形全等的判定优秀课件ppt，共14页。PPT课件主要包含了CONTENTS，学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业等内容，欢迎下载使用。

1.掌握两直角三角形全等的方法：HL. （重点）
已知一个角为90°两个直角三角形。证明两者全等的还有哪些特别的方法？
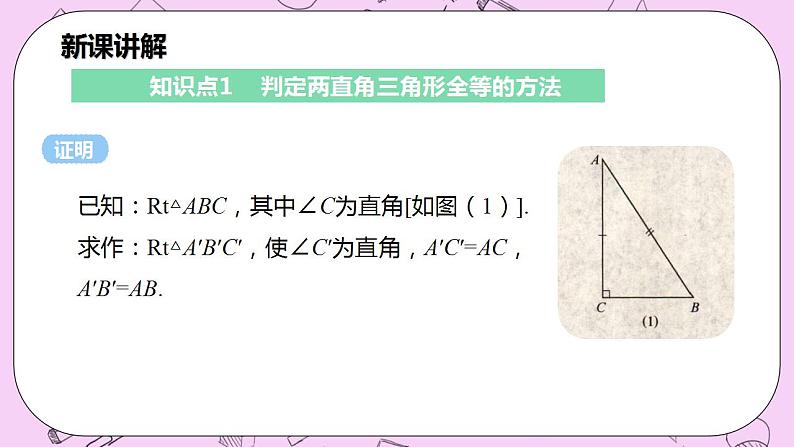
知识点1 判定两直角三角形全等的方法
已知：Rt△ABC，其中∠C为直角[如图（1）].求作：Rt△A′B′C′，使∠C′为直角，A′C′=AC，A′B′=AB.
将画好的Rt△ A′B′C′与Rt△ABC叠一叠，看看它们能否完全重合？由此你能得到什么结论？
作法：（1）作∠MC′N=∠C=90°；（2）在C′M上截取C′A′=CA；（3）以A′为圆心、AB长为半径画弧， 交C′N于点B′；（4）连接A′B′.则Rt△A′B′C′ [如图（2）]就是所求作的直角三角形.
判定两三角形全等的方法：斜边、直角边：1．斜边和一条直角边分别相等的两个直角三角形全等 (简记为“斜边、直角边”或“HL”)．2．(1)书写格式：如图，在Rt△ABC和Rt△A′B′C′中， ∵ ∴Rt△ABC≌Rt△A′B′C′. (2)注意：书写时必须强调直角三角形．
1.已知：如图，∠BAC＝∠CDB＝90°，AC=DB . 求证：AB=DC. 证明：∵ ∠BAC＝∠CDB＝90°，（已知） ∴ △BAC，△CDB都是直角三角形. 又∵AC=DB，（已知） BC=CB，（公共边） ∴Rt△ABC≌Rt△DCB.（HL ） ∴ AB = DC. （全等三角形的对应边相等）
知识点2 直角三角形全等的综合判定
判定直角三角形全等的“四种思路”：(1)若已知条件中有一组直角边和一组斜边分别相等，用 “HL”判定．(2)若有一组锐角和斜边分别相等，用“AAS”判定．(3)若有一组锐角和一组直角边分别相等，①直角边是锐角的对边，用“AAS”判定；②直角边是锐角的邻边，用“ASA”判定．(4)若有两组直角边分别相等，用“SAS”判定．
1.如图，在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF.求证： Rt△ABE≌Rt△CBF. 导引：根据AB＝CB，∠ABE＝∠CBF＝90°，AE＝CF，可利用“HL”证明Rt△ABE≌Rt△CBF.
证明： ∵∠ABC＝90°， ∴∠CBF＝∠ABE＝90°. 在Rt△ABE和Rt△CBF中， ∵AE＝CF，AB＝CB， ∴Rt△ABE≌Rt△CBF(HL)．
2.下列可使两个直角三角形全等的条件是 (　　) A．一个锐角对应相等 　B．两个锐角对应相等 C．一条边对应相等 　 D．两条边对应相等3.如图，OD⊥AB于D，OP⊥AC于P，且OD＝OP，则△AOD与△AOP全等的理由是(　　) A．SSS　　　B．ASA 　C．SSA　　 D．HL