鲁教版 (五四制)七年级上册第三章 勾股定理3 勾股定理的应用举例优质课课件ppt

勾股定理的应用举例（2）

教学目标：

1．  经历运用勾股定理及其逆定理解决实际问题的过程，在数学活动中发展学生的探究意识和合作交流的习惯。

2．  掌握勾股定理及其逆定理和它们的简单应用。

重点难点： 

重点：能熟练运用勾股定理及其逆定理解决实际问题

难点：熟练运用勾股定理及其逆定理解决实际问题

教学过程

复习巩固

1．勾股定理：直角三角形两直角边的平方和等于斜边的平方。即：

c=a+b（c为斜边）。

2．勾股定理的逆定理：如果三角形的三边长a、b、c有下面关系：

a+b= c，那么这个三角形是直角三角形。

 注意：勾股定理是直角三角形的性质定理，而勾股定理的逆定理是直角三角形的判定定理。

讲授新课

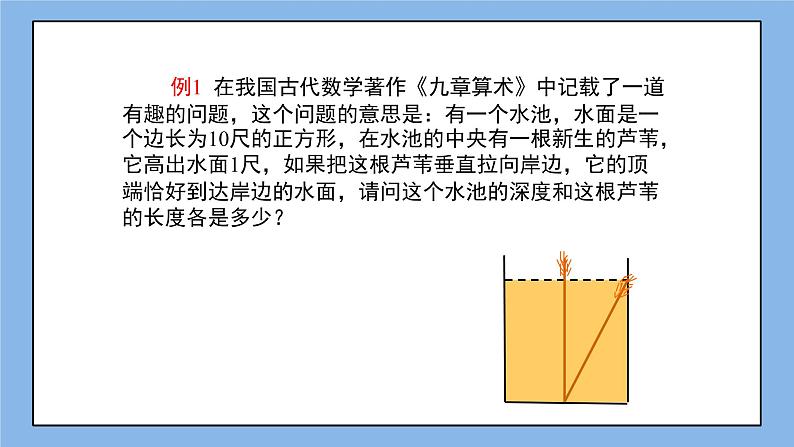
例1  代数学著作《九章算术》中记载了如下一个问题：有一个水池，水面的边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？

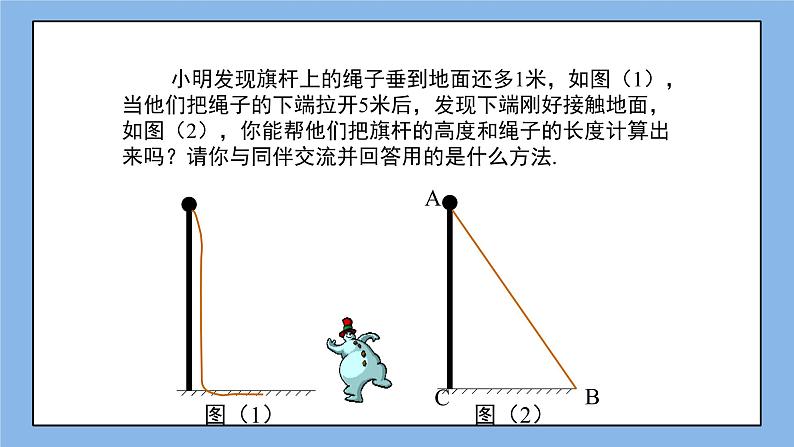
学生独立或合作思考后，会将此问题转化为数学模型，如图设水深为x尺，则芦苇的长度为（x+1）尺。

由勾股定理得x²+5²=(x+1)²;

解得x=12（尺）;x+1=13（尺）

答：水池的水深12尺，这根芦苇长13尺。

例2、如图，某隧道的截面是一个半径为4.2m的半圆形，一辆高3.6m，宽3m的卡车能通过该隧道吗？

解：隧道的横截面如图2，AB的中点O是隧道的截面半圆的圆心。

    OB=1.5m，BC=3.6m，∠ABC为直角

在直角三角形OBC中，由勾股定理得

隧道的截面半径r=4.2m，4.2×4.2=17.64>15.21

故卡车可以沿着该隧道中间顺利通过。

 随堂练习

1．今早7：00，我从家出发，以100米/分的速度向西走5分钟，又以120米/分的速度向南走10分钟， 到达学校。

（1）早上老师共走了多少路程？

（2）家到学校的距离是多少？

2．如图，一座城墙高11.7m，墙外有一个宽为9m的护城河，那么一个长为15m的云梯能否到达墙的顶端？

3．课本随堂练习

课堂小结：学会适当的应用勾股定理。

课后作业

习题3.5—1、3