人教版 (五四制)八年级上册20.1 轴对称精品课件ppt

第二十章    轴对称

20.1  轴对称（第一课时）

20.1.1 轴对称

一、教学目标

（一）学习目标

1.了解轴对称图形和两个图形成轴对称的概念，知道轴对称图形和两个图形成轴对称的区别与联系．

2. 探索两个图形成轴对称的性质，体会由具体到抽象认识问题的过程，感悟类比方法在研究数学问题中的作用．

3. 探索轴对称图形的性质.

（二）学习重点

轴对称图形的概念和性质．

（三）学习难点

轴对称图形和两个图形成轴对称的区别与联系．

二、教学设计

（一）课前设计

1.预习任务

（1）轴对称图形概念：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够__________，这个图形就叫做轴对称图形.

（2）两个图形成轴对称：把一个图形沿着某条直线折叠，如果它能够与另一个图形   ，那么就说这两个图形关于这条直线成轴对称.

【答案】（1）互相重合；（2）重合

2.预习自测

（1）在字母“ABCDEF”中，是轴对称图形的是__________.

【知识点】轴对称概念

【思路点拨】是不是轴对称图形，关键是看沿着某条直线折叠，直线两旁的部分是否能够互相重合.

【答案】 ABCDE

（2）正方形有______条对称轴.

【知识点】轴对称的概念

【思路点拨】除了过正方形两组对边中点的直线外，还有两条对角线所在的直线也是它的对称轴.

【答案】4

（3）成轴对称的两个图形_______（填“全等” 或“不一定全等”）；两个全等的图形   成轴对称（填“一定”或“不一定”）

【知识点】两个图形成轴对称的概念

【思路点拨】两个图形成轴对称，则能完全重合，自然就全等，两个图形全等但不一定沿着某直线折叠后能完全重合.

【答案】“全等” “不一定”

（4）如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的______.

【知识点】轴对称的性质

【思路点拨】根据轴对称的性质

【答案】垂直平分线

(二)课堂设计

1.知识回顾

（1）常见的轴对称图形：线段、角、矩形、等腰三角形、圆等．

（2）轴对称图形的对称轴是直线．

2.问题探究

探究一  轴对称图形和两个图形成轴对称的概念．

问题1：把一张纸对折，剪出一个图案（折痕处不要完全剪断），再打开这张对折的纸，就得到了美丽的窗花，你能发现它们有什么共同特点吗？

师生活动：学生通过观察发现这些图案都是对称的，图形从中间分开后，左右两部分能够完全重合.

师指出：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.这时，我们也说这两个图形关于这条直线成轴对称.

【设计意图】让学生通过观察图片，感知具体的轴对称图形特征，为抽象出轴对称图形的概念作铺垫.

追问：你能举出一些轴对称图形的例子吗？

师生活动：学生思考并举例.

【设计意图】让学生通过举例，对轴对称图形的本质特征进行再认识.

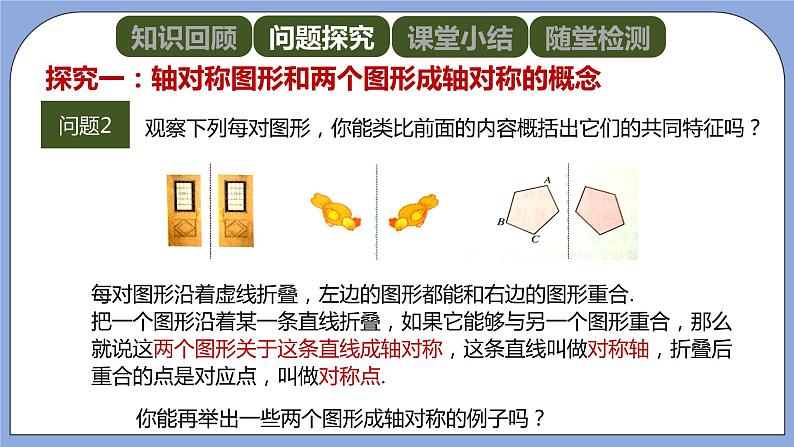
问题2：观察下列每对图形，你能类比前面的内容概括出它们的共同特征吗？

师生活动：学生观察思考，并相互交流，发现其共同特征——每对图形沿着虚线折叠，左边的图形都能和右边的图形重合.教师进一步说明：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线成轴对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点.

【设计意图】让学生观察具体实例，类比轴对称图形概念的学习过程，发现两个图形成轴对称的特征，进而概括出轴对称的概念.

追问1：你能再举出一些两个图形成轴对称的例子吗？

师生活动：学生思考并回答.

【设计意图】让学生通过举例，对轴对称的本质特征进行再认识.

追问2：你能结合具体图形说明轴对称图形和两个图形成轴对称有什么区别和联系吗？

师生活动：学生独立思考后，进行交流，然后学生代表发言.教师根据学生回答情况进行评价，如果学生有困难，可以适时追问下面的问题：

（1）        成轴对称的两个图形全等吗？

（2）        如果把一个图形沿对称轴分成两个图形，那么这两个图形全等吗？这两个图形对称吗？

师生共同归纳得出，把成轴对称的两个图形看成一个整体，它就是一个轴对称图形，把一个轴对称图形沿着对称轴分成两个图形，这两个图形关于这条对称轴对称.

【设计意图】让学生知道轴对称图形和两个图形成轴对称的本质是一致的，但同时两者也是有区别的，轴对称图形指的是一个图形沿对称轴折叠后这个图形的两部分能完全重合，而两个图形成轴对称是指两个图形之间的位置关系，这两个图形沿对称轴折叠后能够重合.

探究二 探索成轴对称的两个图形的性质

问题1   如图，△ABC 和△关于直线MN对称，点A′，B′，C′分别是点A，B，C的对应点，线段AA′，BB′，CC′与直线MN有什么关系？

师生活动：学生尝试回答，并相互补充，最后得出：线段AA′，BB′，CC′都与直线MN垂直，同时MN平分线段AA′，BB′，CC′.

追问1：你能说明其中的道理吗？

师生活动：学生独立思考，学生代表发言，师生共同交流，教师关注学生能否从两个图形成轴对称的定义出发，发现折叠后点A与A′重合，进而得到PA=PA′；能否发现折叠后∠APM，∠A′PM的顶点是重合的，进而得出这两个角相等，AA′与MN垂直.同理，BB′，CC′与MN也垂直.

【设计意图】从特例出发，让学生经历发现结论，说明结论的过程，体会概念在探索性质中的重要作用.

追问2：前面的例子说明“如果△ABC 和△A′B′C′关于直线MN对称，那么直线MN垂直平分线段AA′，BB′，CC′”，如果将“三角形”改为“四边形”“五边形”……其它条件不变，上述结论还成立吗？

师生活动：教师提出问题，学生独立思考，然后小组讨论，学生代表发言.学生类比前面的研究过程得出结论，说明结论.教师指出：经过线段中点且垂直于这条线段的直线，叫做这条线段的垂直平分线.

【设计意图】拓展问题研究范围，将问题一般化.让学生经历由特殊到一般地探索问题的过程，体会研究问题的一般化方法和类比方法.

追问3：你能用数学语言概括前面的结论吗？

师生活动：学生尝试概括，并相互补充，得出成轴对称的两个图形的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.教师引导学生将成轴对称的两个图形的性质用其它方式表述，即对称点所连线段被对称轴垂直平分；对称轴垂直平分对应点所连线段.

【设计意图】培养学生的抽象概括能力，提高学生对成轴对称的两个图形的性质的认识.

探究三 探索轴对称图形的性质

问题1：下图是一个轴对称图形，你能发现什么结论？能说明理由吗？

师生活动：学生类比成轴对称的两个图形的性质的探究过程和方法发现结论：直线垂直平分线段AA′，BB′或直线是线段AA′，BB′的垂直平分线，然后说明理由.

追问：你能用数学语言概括前面的结论吗？

师生活动：学生尝试概括，并相互补充，得出轴对称图形的性质.

【设计意图】让学生在探索成轴对称的两个图形的性质上，探索轴对称图形的性质，体会类比方法在研究数学问题中的作用.

练习：(教科书第60页练习第1、2题)

1.如图所示的每个图形都是轴对称图形吗？如果是，指出它的对称轴.

（1）        （2）       （3）    （4）    （5）

【知识点】轴对称图形的概念

【思路点拨】判断一个平面图形是不是轴对称图形，关键看这个图形沿着某条直线折叠后能否完全重合.

【解题过程】略

【答案】(1)（2）（3）（5）是轴对称图形，对称轴略.

2.如图所示的每幅图形中的两个图形是轴对称的吗？如果是，指出它们的对称轴.

【知识点】成轴对称的两个图形的性质

【思路点拨】判断两个图形是不是成轴对称，关键看其中一个图形沿着某条直线折叠后能否与另一个图形完全重合.此外，对称轴的确定，要先找到一对对应点，然后画这条对应点连线段的垂直平分线.

【答案】（1）（3）是轴对称图形，对称轴略.

师生活动：学生口答，并画出对称轴，标注它们的一对对应点.

【设计意图】让学生进一步加强对轴对称概念和性质的认识.

3. 课堂总结

知识梳理

（1）轴对称图形的概念：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够完全重合，这个图形就叫做轴对称图形，这条直线叫做对称轴.

（2）两个图形成轴对称：把一个图形沿着某条直线折叠，如果它能够与另一个图形完全重合，那么就说这两个图形关于这条直线成轴对称.

（3）轴对称图形和两个图形成轴对称的区别和联系：轴对称图形和两个图形成轴对称的本质是一致的，但同时两者也是有区别的，轴对称图形指的是一个图形沿对称轴折叠后这个图形的两部分能完全重合，而两个图形成轴对称是指两个图形之间的位置关系，这两个图形沿对称轴折叠后能够重合.

（4）轴对称图形和成轴对称的两个图形的性质：对应点的连线段被对称轴垂直平分.

重难点归纳

（1）轴对称图形和两个图形成轴对称的区别和联系：轴对称图形和两个图形成轴对称的本质是一致的，但同时两者也是有区别的，轴对称图形指的是一个图形沿对称轴折叠后这个图形的两部分能完全重合，而两个图形成轴对称是指两个图形之间的位置关系，这两个图形沿对称轴折叠后能够重合.

（2）判定一个图形是不是轴对称图形或两个图形是否成轴对称的关键：把这个图形或这两个图形沿着某条直线折叠，看直线两旁的部分是否完全重合.

（三）课后作业

基础型自主突破

1．下列图形中，轴对称图形的个数是（   ）

A．1个    B．2个    C．3个      D．4个

【知识点】轴对称的概念

【解题过程】略

【思路点拨】把上述图形分别沿着某条直线折叠，看直线两旁的部分是否完全重合.

【答案】C

2．下列交通标识中，不是轴对称图形的是（　　）

　   A．            B．            C．         D．

【知识点】轴对称的概念

【解题过程】略

【思路点拨】把上述图形分别沿着某条直线折叠，看直线两旁的部分是否完全重合.

【答案】C

3．（2016•绍兴）我国传统建筑中，窗框（如图1）的图案玲珑剔透、千变万化，窗框一部分如图2，它是一个轴对称图形，其对称轴有（  ）

A．1条 B．2条 C．3条 D．4条

【知识点】轴对称概念、性质

【解题过程】解：如图所示，有两条对称轴.

【思路点拨】先确定对应点，再连接对应点之间的线段，最后画出对应点之间线段的垂直平分线.

【答案】B

4．(2016·赤峰)下列图形是由我们熟悉的一些基本数学图形组成的，其中是轴对称图形的是                  （填序号）

【知识点】轴对称概念

【解题过程】略

【思路点拨】把上述图形分别沿着某条直线折叠，看直线两旁的部分是否完全重合.

【答案】①②③④

5．图1中的三角形4与三角形       成轴对称（填编号），整个图形      轴对称图形（填“是”或“不是”），它有      条对称轴.

【知识点】轴对称和两个图形成轴对称的概念

【解题过程】如图2

【思路点拨】把4与1组合，4与2组合，4与3组合，看是否能找到一条直线，沿这条直线折叠，直线两旁的部分能够完全重合.

【答案】1和3；是；2.

6. 如下书写的四个汉字，其中为轴对称图形的是（　　）．

A．   　 B．   　 C.       D.

【知识点】轴对称的概念

【解题过程】略

【思路点拨】根据轴对称的概念，把上述汉字沿某条直线折叠，看直线两旁的部分能否完全重合,很明显，“善”符合要求.

【答案】B

能力型  师生共研

7．如图，直线是五边形ABCDE的对称轴，∠A=130°，∠B=90°，则∠BCD=    .

【知识点】轴对称的性质

【解题过程】

解：如图，∵五边形ABCDE是轴对称图形，是其对称轴，设直线与AE交于点F，

          ∴四边形ABCF与四边形EDCF全等

            垂直平分线段AE

          ∴∠A=∠E=130°∠B=∠D=90°

            ∠AFC=∠EFC=90°

          ∵四边形内角和为360°

          ∴∠BCF=∠DCF=50°

          ∴∠BCD=100°

【思路点拨】利用轴对称的性质进行分析

【答案】100°

8．如图是一台球桌面示意图．图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动．经桌边反弹最后进入球洞的序号是（　　）．

　 A．②      B．①     C．⑥　  D．⑤

【知识点】轴对称的性质

【解题过程】解：如图所示

【思路点拨】根据平面镜反射原理（入射角等于反射角）即黑球以一个怎样的角度去撞击台球桌边沿，就以怎样的角度被反弹出去，因此进入①.

【答案】B

探究型 多维突破

9．如图，在的正方形网格中，已将图中的四个小正方形涂上阴影，若再从其余小正方形中任选一个也涂上阴影，使得整个阴影部分组成的图形成轴对称图形．那么符合条件的小正方形共有（    ）

A．1个         B．2个       C．3个        D．4个

【知识点】轴对称的概念和性质

【解题过程】略

【思路点拨】根据轴对称的概念可以发现:如下图的三个黑色正方形处添上阴影均可使得整个图形组成轴对称图形.

【答案】C

10．如图，在Rt△ABC中，∠ACB=90°，∠A=28°，是上一点，将RT△ABC沿CD折叠，使点落在AC边上的处，求的度数.

【知识点】轴对称图形的性质

【解题过程】解：∵折叠

                ∴△CBD≌△

                ∵∠ACB=90°，∠A=28°

                ∴∠B=∠=62°

                ∴∠AD=62°—28°=34°

【思路点拨】由直角三角形两锐角互余可得∠B=62°，由折叠可以得到△CBD≌△CB′D，进而得到∠B=∠CB′D=62°，再利用三角形的一个外角等于它不相邻的两个内角和求出∠ADB′=62°—28°=34°.

【答案】34°

自助餐

1． 下列学习用具中，不是轴对称图形的是（   ）

A.           B.          C.            D.

【知识点】 轴对称的概念

【解题过程】略

【思路点拨】把上述图形沿着某一直线折叠，看直线两旁的部分能否完全重合，显然C无论怎样折叠都不能实现直线两旁的部分完全重合.

【答案】C

2．下列图形中，是轴对称图形的是（　　）

A.                B.                 C.                  D.

【知识点】轴对称的概念

【解题过程】图形A中，顺着箭头的方向的直线折叠，直线两旁的部分能够完全重合，所以A是轴对称图形.

【思路点拨】把上述图形沿着某一直线折叠，看直线两旁的部分能否完全重合，显然B、C、D无论怎样折叠都不能实现直线两旁的部分完全重合.

【答案】A

3．已知以下四个汽车标志图案：

其中不是轴对称图形的图案是       （只需填入图案代号）． 

【知识点】轴对称图形的概念

【解题过程】略

【思路点拨】①③均可沿着一定的直线折叠后，使得直线两旁的部分能够完全重合，而②④均不能实现.

【答案】②④

4．在图形：正方形、等边三角形、等腰三角形、线段中，对称轴最多的是        .

【知识点】轴对称的概念

【解题过程】解：正方形有4条对称轴，等边三角形有3条对称轴，等腰三角形有1条对称轴，线段有2条对称轴，所以对称轴最多的是正方形.

【思路点拨】分别画出上述四种图形，并逐个找出它们的对称轴，再比较即可.

【答案】正方形.

5. 如图，△ABC中，∠ABC=90°，沿CD折叠△CBD,使点B恰好落在AC边上的点E处，若∠A=26°，则∠CDB等于_________.

【知识点】轴对称图形的性质

【解题过程】解：∵折叠

                ∴△CBD≌△CED

                ∵∠ACB=90°，∠A=26°

                ∴∠B=∠CED=64°，∠BCD=∠ECD=45°

                ∵∠BCD+∠BDC+∠B=180°

 ∴∠CDB=180°—64°—45°=71°

【思路点拨】由直角三角形两锐角互余可得∠B=64°，由折叠可以得到△CBD≌△CED，进而得到∠B=∠CED=64°，∠BCD=∠ECD=45°，再利用三角形内角和求出∠CDB=71°.

【答案】71°

6. 如图，将△ABC沿直线折叠后，使得点与点重合，已知AC=5cm，△ADC的周长为13cm，求BC的长．

【知识点】轴对称图形的性质

【解题过程】解：∵折叠

                ∴△ADE≌△BDE

                ∴AD=BD

                ∵AC+AD+CD=13cm

 ∴AC+CB=13cm

 ∵AC=5cm

 ∴BC=8cm

【思路点拨】由折叠可以得到△ADE≌△BDE，进而得到AD=BD，因为AC+AD+CD=13cm，

所以，AC+CB=13cm，所以，BC=13-5=8cm.

【答案】BC=8cm