









数学八年级上册20.1 轴对称获奖课件ppt
展开20.1.2 线段的垂直平分线的性质
(1)轴对称的概念:如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形.(2)两个图形成轴对称:把一个图形沿着某条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称.(3)线段的垂直平分线:经过线段中点且垂直于这条线段的直线叫做线段的垂直平分线.
问题1:分别量一量点P1,P2,P3,…到点A与点B的距离,你有什么发现? 相等
如图,直线l垂直平分线段AB,P1,P2,P3,…是l上的点
探究一:线段垂直平分线的性质
活动1
整合旧知,探究线段垂直平分线的性质
问题2:把上图沿着直线l折叠,你有什么发现? 线段P1A与P1B,P2A与P2B,P3A与P3B重合.
问题3:P1A=P1B,P2A=P2B,P3A=P3B,你能从推理的角度给出证明吗?
探究一:线段垂直平分线的性质
证明:∵l⊥AB ∴ ∠PCA=∠PCB 在△PAC和△PBC中 AC=BC ∠PCA=∠PCB PC=PC ∴△PAC≌△PBC ∴ PA=PB
如图,直线l⊥AB,垂足为C,AC=BC ,点P在l上. 求证:PA=PB
探究一:线段垂直平分线的性质
重点、难点知识★▲
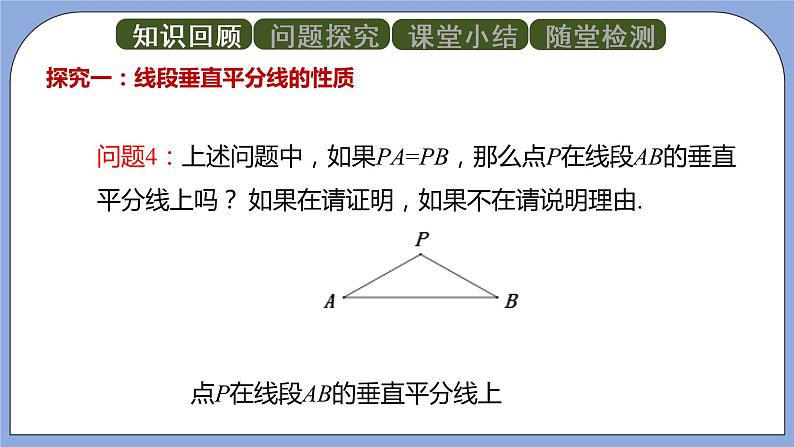
问题4:上述问题中,如果PA=PB,那么点P在线段AB的垂直平分线上吗? 如果在请证明,如果不在请说明理由.
点P在线段AB的垂直平分线上
探究一:线段垂直平分线的性质
∴∠PCA=∠PCB=90°在Rt△PAC和Rt△PBC中 PA=PBPC=PC∴Rt△PAC≌Rt△PBC∴AC=BC∴点P在线段AB的垂直平分线上
证明:过点P作PC⊥AB于点C,
点P在线段AB的垂直平分线上
探究一:线段垂直平分线的性质
问题5:上述问题中,辅助线的添加还有别的方法吗?
反思刚才的辅助线添加方法,是作垂直证明点C 是中点,是否可以连接点P和AB的中点,证明PC垂直AB呢?
可以
探究一:线段垂直平分线的性质
证明:连接点P与AB的中点C, ∵点C 是AB中点 ∴ AC=BC在△PAC和△PBC中 PA=PB PC=PC AC=BC ∴△PAC≌△PBC ∴∠PCA=∠PCB=90° ∴点P在线段AB的垂直平分线上
探究一:线段垂直平分线的性质
问题6:反思PA=PB,可以得到点P在线段AB的垂直平分线上,平面内,像点P这样的点有多少个?它们有怎样的特征?
到线段两端距离相等的点在这条线段的垂直平分线上
探究一:线段垂直平分线的性质
1.通过前面的探究,我们知道线段垂直平分线的性质:线段垂直平分线上的点到线段两端的距离相等;到线段两端距离相等的点在这条线段的垂直平分线上.2.求两条线段相等的方法:通常将所求线段设法转化到两个三角形中,利用三角形全等来解决.
探究二:运用线段垂直平分线的性质
活动1
线段垂直平分线的性质
例1 如图,在△ABC中,AC的垂直平分线ED交AC于点E,交AB于点D,CE=4,△BCD的周长为16,则△ABC的周长是______ .
解:∵ED是线段AC的垂直平分线, CE=4∴DC=DA,CE=AE=4∵△BCD的周长为16∴DC+DB+BC=16∴DA+DB+BC=16,即CB+AB=16∴△ABC的周长为16+8=24
【思路点拨】由线段垂直平分线的定义可知DC=DA,CE=AE=4,DC+DB+BC=DA+DB+BC=16,所以△ABC的周长为16+8=24.
探究二:运用线段垂直平分线的性质
练习:如图,AD垂直平分线段BC,点C在AE的垂直平分线上. 则线段AB、BD、DE之间的数量关系是_________.
解:∵AD垂直平分线段BC∴BD=CD,AB=AC∵点C在AE的垂直平分线上∴CA=CE∴AB+BD=AC+CD=CE+CD=DE
【思路点拨】由线段垂直平分线的性质可得:BD=CD,AB=AC,CA=CE,所以AB+BD=AC+CD=CE+CD=DE.
探究二:运用线段垂直平分线的性质
探究二:运用线段垂直平分线的性质
活动2
线段垂直平分线的判定
例2 如图,已知PA=PB,QA=QB. 求证:直线PQ垂直平分线段AB.
方法1证明:在△PAQ和△PBQ中 ∴△PAQ≌△PBQ ∴∠APQ=∠BPQ在△PAC和△PBC中 ∴△PAC≌△PBC∴ AC=BC,∠ACP=∠BCP=90°∴ 直线PQ垂直平分线段AB
例2 如图,已知PA=PB,QA=QB. 求证:直线PQ垂直平分线段AB.
探究二:运用线段垂直平分线的性质
方法2证明:∵PA=PB, ∴点P在线段AB的垂直平分线上 ∵QA=QB. ∴点Q在线段AB的垂直平分线上 ∴直线PQ垂直平分线段AB
【思路点拨】由三角形全等或线段垂直平分线的判定可以直接得出结论.
练习:如图,AD、BC相交于点O,OA=OC,∠A=∠C,BE=DE. 求证:OE垂直平分BD.
证明:在△AOB和△COD中 ∠A=∠C OA=OC ∠AOB=∠COD ∴△AOB≌△COD ∴OB=OD ∴点O在线段BD的垂直平分线上 ∵BE=DE ∴点E在线段BD的垂直平分线上 ∴OE垂直平分BD
探究二:运用线段垂直平分线的性质
例1 已知:直线AB和AB 外一点P. 求作:AB的垂线,使它经过点P.
作法:1.任意取一点Q,使P、Q在AB的两旁. 2.以P为圆心,PQ长为半径画弧,交直线AB于点C、D. 3.分别以C、D为圆心,大于 CD的长为半径画弧,两弧交于点E. 4.作直线PE. 直线PE即为所求.
探究三:利用线段垂直平分线的性质作图
活动1
过一点作已知直线的垂线
练习:已知:直线AB上一点P. 求作:AB的垂线,使它经过点P.
作法: 1.以P为圆心,任意长为半径画弧,交直线AB于点C、D. 2.分别以C、D为圆心,大于 CD的长为半径画弧,两弧交于点E、F. 3.作直线EF. 直线EF即为所求.
探究三:利用线段垂直平分线的性质作图
例2 如图所示的五角星图案是一个轴对称图形,你能作出它的一条对称轴吗?
作法: 1.确定并连接轴对称图形的一对对应点. 2.作所连线段的垂直平分线对应点所连线段的垂直平分线即为所求.
探究三:利用线段垂直平分线的性质作图
活动2
作轴对称图形的对称轴
【思路点拨】因为轴对称图形沿着对称轴折叠能够完全重合,所以作对应点所连线段的垂直平分线即为轴对称图形的对称轴.
练习:如图,在直线AB的同一侧有A、B两点,在直线l上确定一点P,使得点P到A和B的距离相等.
作法: 1.连接AB. 2.作线段AB 的垂直平分线,交直线l于点P . 所以,点P为所求.
【思路点拨】到线段AB两端的距离相等,说明点P在线段AB的垂直平分线上,要在直线l上,说明线段AB的垂直平分线与直线l的交点就正好满足要求.
探究三:利用线段垂直平分线的性质作图
知识梳理
(1)线段垂直平分线的性质: 线段垂直平分线上的点到线段两端的距离相等. 到线段两端距离相等的点在这条线段的垂直平分线上.(2)过一点作已知直线的垂线的方法.(3)作轴对称图形的对称轴的方法:连接一对对应点,作对应点所连线段的垂直平分线.
重难点归纳
线段垂直平分线的性质: 线段垂直平分线上的点到线段两端的距离相等. 到线段两端距离相等的点在这条线段的垂直平分线上.
点击“随堂训练→名师训练”选择“《线段的垂直平分线的性质》随堂检测 ”
初中人教版 (五四制)22.3 分式方程优质课件ppt: 这是一份初中人教版 (五四制)22.3 分式方程优质课件ppt,文件包含人教版五四学制八上数学223分式方程第2课时课件pptx、人教版五四学制八上数学223分式方程第2课时教案doc等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
数学八年级上册22.1 分式优秀ppt课件: 这是一份数学八年级上册22.1 分式优秀ppt课件,文件包含人教版五四学制八上数学2222分式的加减第2课时教案doc、人教版五四学制八上数学2222分式的加减第2课时课件ppt等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中人教版 (五四制)22.1 分式试讲课ppt课件: 这是一份初中人教版 (五四制)22.1 分式试讲课ppt课件,文件包含人教版五四学制八上数学2221分式的乘除第2课时课件pptx、人教版五四学制八上数学2221分式的乘除第2课时教案doc等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。













